【小结】JOISC 2021 Final

T1： とてもたのしい家庭菜園 4

区间加，比较套路的做法是差分，转化为单点加。

单峰序列等价于差分序列存在一个断点，断点之前都是正整数，断点之后都是负整数。

我们枚举一下断点即可。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define pre(i,a,b) for(int i=a;i>=b;i--)
#define N 200005
using namespace std;
int n,a[N];long long p[N],q[N];
int main(){
	scanf("%d",&n);
	rep(i,1,n)scanf("%d",&a[i]);
	rep(i,1,n-1)a[i]=a[i+1]-a[i];
	rep(i,1,n-1)p[i]=p[i-1]+max(0,1-a[i]);
	pre(i,n-1,1)q[i]=q[i+1]+max(0,a[i]+1);
	long long mn=0x7fffffffffffffffLL;
	rep(i,1,n)mn=min(mn,max(p[i-1],q[i]));
	printf("%lld\n",mn);
	return 0;
}

T2：雪玉

提供一个好想的方法。

观察到对于第 \(i\) 个雪球，跨过第 \(i-1\) 或第 \(i+1\) 个雪球的贡献为零。

所以我们只用考虑相邻两个雪球之间的一段，多少属于左端点，多少属于右端点。

断点具有单调性，我们直接二分答案即可。

时间复杂度 \(\mathcal{O}(N\log Q)\) 。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define pre(i,a,b) for(int i=a;i>=b;i--)
#define N 200005
#define int long long
using namespace std;
int n,m,ll[N],rr[N],a[N],ans[N];
void calc(int x,int len){
	if(ll[m]+rr[m]<=len){ans[x]+=rr[m],ans[x+1]+=ll[m];return ;}
	int l=1,r=m,ed=m;
	while(l<=r){
		int mid=(l+r)>>1;
		if(ll[mid]+rr[mid]>len)ed=mid,r=mid-1;
		else l=mid+1;
	}
	if(ll[ed]==ll[ed-1])ans[x+1]+=ll[ed],ans[x]+=len-ll[ed];
	else ans[x]+=rr[ed],ans[x+1]+=len-rr[ed];
}
signed main(){
	scanf("%lld%lld",&n,&m);
	rep(i,1,n)scanf("%lld",&a[i]);
	int cur=0;
	rep(i,1,m){
		int x;scanf("%lld",&x);cur+=x;
		ll[i]=max(ll[i-1],-cur);
		rr[i]=max(rr[i-1],cur);
	}
	ans[1]+=ll[m];ans[n]+=rr[m];
	rep(i,1,n-1)calc(i,a[i+1]-a[i]);
	rep(i,1,n)printf("%lld \n",ans[i]);
	return 0;
} 

T3：集合写真

\(a_i<a_{i+1}+2\)，等价于 \(a_i-1\le a_{i+1}\) 。

如果我们将 \(a_i\) 看成台阶，那么每次最多只能下降一个。

所以满足条件的排列一定可以分成若干段连续下降的台阶。

我们定义状态 \(f[i]\) 表示前 \(i\) 个数合法的最小代价。

转移方程为 \(f[i]=\min\limits_{0\le j<i}\{f[j]+calc(j+1,i)\}\) 。

其中代价函数 calc(l,r) 表示将区间 \([l,r]\) 还原成一个下降的台阶的最小代价。

由于是邻项交换，所以考虑逆序对。

分开讨论。

对于 \(<l\) 的数，在 \(f[l-1]\) 中已经考虑过了，直接忽略。

对于 \(\ge l\) 并 \(\le r\) 的数，计算顺序对 \(i<j\) 且 \(a_i <a_j\) 的个数。

对于 \(>r\) 的数，只会与在它后面的 \(\le r\) 的数产生贡献。

直接 \(\mathcal{O}(N^2)\) 计算 calc 函数，总时间复杂度 \(\mathcal{O}(N^4)\) ，可以得到 \(44\) 分。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define pre(i,a,b) for(int i=a;i>=b;i--)
#define N 5005
using namespace std;
int n,a[N],f[N];
int calc(int l,int r){
	int sum=0;
	rep(i,1,n)rep(j,i+1,n){
		if(a[i]<l||a[j]<l)continue;
		if(a[i]>r&&a[j]>r)continue;
		if(a[i]<=r&&a[j]<=r)sum+=a[i]<a[j];
		else if(a[i]>r)sum++;
	}
	return sum;
}
int main(){
	scanf("%d",&n);
	rep(i,1,n)scanf("%d",&a[i]);
	memset(f,0x3f,sizeof(f));f[0]=0;
	rep(i,1,n)rep(j,0,i-1)f[i]=min(f[i],f[j]+calc(j+1,i));
	printf("%d\n",f[n]);
	return 0;
}

观察一下发现 calc 函数本质上还是计算逆序对，用两个树状数组维护一下即可。

我们可以通过 calc(l,r) 基础上加一个数快速计算 calc(l,r+1) ，总时间复杂度 \(\mathcal{O}(N^2\log N)\) 。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define pre(i,a,b) for(int i=a;i>=b;i--)
#define N 5005
using namespace std;
int c[2][N],n,a[N],f[N],mat[N];
inline void add(int op,int x,int y){for(;x<=n;x+=x&-x)c[op][x]+=y;}
inline int ask(int op,int x){int sum=0;for(;x;x-=x&-x)sum+=c[op][x];return sum;}
int main(){
	scanf("%d",&n);
	rep(i,1,n)scanf("%d",&a[i]),mat[a[i]]=i;
	memset(f,0x3f,sizeof(f));f[0]=0;
	rep(i,0,n-1){
		memset(c,0,sizeof(c));
		int sum=0;
		rep(j,i+1,n)add(1,mat[j],1);
		rep(j,i+1,n){
			sum+=2*ask(0,mat[j])+i+ask(1,mat[j])-j;
			add(1,mat[j],-1);add(0,mat[j],1);
			f[j]=min(f[j],f[i]+sum);
		}
	}
	printf("%d\n",f[n]);
	return 0;
}

T4：ロボット

如果当前边已经是唯一的边，那么我们可以直接连一条边权为 \(0\) 的有向边。

否则我们可以花费 \(P_i\) 的代价将它变成唯一的边，所以我们连一条边权为 \(P_i\) 的有向边。

然后跑最短路，得到 $0 $ 分的好成绩（

手算以下发现还有两类情况没有考虑到。

首先 \(P_i\) 可以不相等，这意味着我们可以保留当前边，然后花费其它多条边的代价使之成为唯一边可能会更优。

还有一种情况就是例如 \(1-2\) ，\(2-3\) ，两条边颜色相同，只用任意改动一条边就能使两条边同时成为唯一边。

扩展以下，我们将直接花费 \(P_i\) 代价改变一条边的操作为 \(\mathbf{A}\) 操作，保留当前边而修改其他所有边的操作为 \(\mathbf{B}\) 操作。

那么先进行 \(\mathbf{A}\) 操作，再进行 \(\mathbf{B}\) 操作，第一次 \(\mathcal{A}\) 操作的代价可以省去。

所以对于每条边建立一个虚点，进入这个虚点表示进行一次 \(\mathbf{A}\) 操作，离开这个虚点表示进行一次 \(\mathbf{B}\) 操作 ，然后进行连边操作。

一共 \(N+M\) 个点，\(8M\) 条有向边，时间复杂度 \(\mathcal{O}((N+M)\log (N+M))\) 。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define pre(i,a,b) for(int i=a;i>=b;i--)
#define N 500005
using namespace std;
int n,m,h[N],tot,v[N],idx;long long d[N],c[N<<1];map<int,int>u[N];
struct edge{int to,nxt;long long val;}e[N<<2];
void add(int x,int y,long long z){e[++tot].nxt=h[x];h[x]=tot;e[tot].to=y;e[tot].val=z;}
struct node{int y,c,p;};vector<node>a[N];
priority_queue<pair<long long,int> >q;
void dij(){
	memset(d,0x3f,sizeof(d));d[1]=0;q.push(make_pair(0,1));
	while(!q.empty()){
		int x=q.top().second;q.pop();v[x]=1;
		for(int i=h[x];i;i=e[i].nxt)if(d[x]+e[i].val<d[e[i].to])
			d[e[i].to]=d[x]+e[i].val,q.push(make_pair(-d[e[i].to],e[i].to));
		while(!q.empty()&&v[q.top().second])q.pop();
	}
}
int main(){
	scanf("%d%d",&n,&m);idx=n;
	rep(i,1,m){
		int x,y,z,w;scanf("%d%d%d%d",&x,&y,&z,&w);
		node cur;cur.y=y;cur.c=z;cur.p=w;
		a[x].push_back(cur);cur.y=x;a[y].push_back(cur);
	}
	rep(x,1,n){
		for(int i=0;i<(int)a[x].size();i++)if(!c[a[x][i].c])u[x][a[x][i].c]=++idx,c[a[x][i].c]=1;
		for(int i=0;i<(int)a[x].size();i++)c[a[x][i].c]=0;
	}
	rep(x,1,n){
		for(int i=0;i<(int)a[x].size();i++)c[a[x][i].c]+=a[x][i].p;
		for(int i=0;i<(int)a[x].size();i++){
			add(x,a[x][i].y,a[x][i].p);
			add(x,a[x][i].y,c[a[x][i].c]-a[x][i].p);
			add(u[x][a[x][i].c],a[x][i].y,c[a[x][i].c]-a[x][i].p);
			add(x,u[a[x][i].y][a[x][i].c],0);
		}
		for(int i=0;i<(int)a[x].size();i++)c[a[x][i].c]=0;
	}
	dij();printf("%lld\n",d[n]==0x3f3f3f3f3f3f3f3fLL?-1LL:d[n]);
	return 0;
} 

T5：ダンジョン 3

贪心神题。

手算一下不难得到 \(\mathcal{O}(N^2)\) 的贪心。

我们从 \(S\) 点出发，每次选择与当前点距离 \(\le U\) 的 \(B\) 最小的点，如果这个点的 \(B\) 比当前点小，则将能量填充至恰好到达该点，否则就将燃料填满。

直接二分可以做到 \(\mathcal{O}(N^2)\) ,离线一下可以 \(\mathcal{O}(N^2)\) 。

接下来是最关键的模型转换，我们将这个过程转化为线段覆盖的模型。

对于每一层，我们看成数轴上的一个点，相邻两点的距离就是 \(A\) 。我们将第 \(i\) 个点的位置记作 \(S_i\)

对于在第 \(i\) 层恢复 \(j\) 的能量，相当于以 \(B_i\) 的单位代价覆盖线段 \([S_i,S_i+j]\) 。

\(U_i\) 的限制条件，相当于以 \(B_i\) 的单位代价，只能选择覆盖线段 \([S_i,S_i+U_i]\) 。

注意上面的覆盖不一定从 \(S_i\) 开始，因为开始一段可以被前面的点覆盖。

那么如果 \(U\) 是定值，我们只用开一个栈维护覆盖每个区间的最小的代价。时间复杂度 \(\mathcal{O}(N\log N)\) 。

接着考虑子任务 \(3\) ， \(T_{i}=N+1\)，非常明显地提示了考虑对询问按 \(S\) 从大到小排序的离线。

\(U\) 会变化，考虑观察一下当 \(S,T\) 固定事，随着 \(U\) 的变化答案会怎么变。

随着 \(U\) 的增大，答案越来越小，对于每一层，都是先慢慢覆盖后面的一段，然后停滞不前，接着被前面更优的层覆盖（如果存在更优的），最后被完全覆盖。

这四部分都是关于 \(U\) 的一次函数。

第一部分是形如 \(y=kx(k>0)\) 的函数，对应的区间是从 \(0\) 开始一直到，第 \(i\) 层在碰到后面第一个 \(B_j<B_i\) 的 \(j\) 层之后停止。

第二部分是形如 \(y=a\) 的函数，\(a\) 是常数，对应的区间是停止向后扩展，但还没有被前面更优的区间覆盖。

第三部分是形如 \(y=kx+b(k<0)\) ，的函数，对应的区间是当前层正在被前面第一个 \(\le B_i\) 的区间覆盖。

被完全覆盖后的贡献为 \(0\) ，这一部分可以省略。

这样我们运用子任务 \(2\) 的单调栈找出每一层前面和后面的更优区间。然后倒叙枚举当前区间，用树状数组维护这若干个分段函数的和。

具体操作是用两个树状数组维护每一个位置此时的斜率和截距，\(U\) 的范围很大，需要离散化。

对于 \(T_i\) 任意的情况，考虑转化为子任务 \(3\) 。

我们发现在 \([S_i,T_i]\) 中与 \(T_i\) 的距离 \(\le U_i\) 且 \(B\) 最小的位置 \(x\) ，覆盖 \([x,N+1]\) 时在 \(T_i\) 后面的覆盖方案与 \([S_i,N+1]\) 相同，在\(T_i\) 前面时是连续的一段，前者是子任务 \(3\) ，后者可以 \(\mathcal{O(1)}\) 求得。所以我们只用先二分出对应区间，然后用 ST表 找出位置 \(x\) 。

这里给一章官方题解的图。

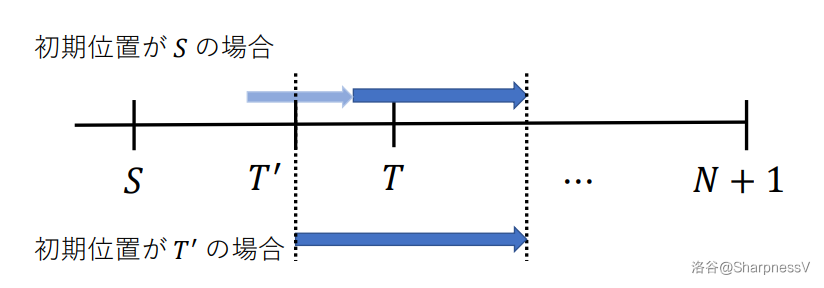
时间复杂度 \(\mathcal{O}(N\log N)\) 。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define pre(i,a,b) for(int i=a;i>=b;i--)
#define N 200005
#define int long long
using namespace std;
int n,m,a[N],b[N],t,lg[N],c[2][N],o[N],u[N],T,s[N],sta[N],top,pr[N],nx[N],ans[N];
struct node{int s,t,u;}q[N];
namespace st1{
	int f[N][20];
	inline int ck(int x,int y){if(b[x]<b[y])return x;return y;}
	int ask(int l,int r){int cur=lg[r-l+1];return ck(f[l][cur],f[r-(1<<cur)+1][cur]);}
	void init(){
		rep(i,1,n+1)f[i][0]=i;
		rep(j,1,t)rep(i,1,n-(1<<j)+2)f[i][j]=ck(f[i][j-1],f[i+(1<<(j-1))][j-1]);
	}
}
namespace st2{
	int f[N][20];
	inline int ck(int x,int y){if(a[x]>a[y])return x;return y;}
	int ask(int l,int r){int cur=lg[r-l+1];return ck(f[l][cur],f[r-(1<<cur)+1][cur]);}
	void init(){
		rep(i,1,n+1)f[i][0]=i;
		rep(j,1,t)rep(i,1,n-(1<<j)+2)f[i][j]=ck(f[i][j-1],f[i+(1<<(j-1))][j-1]);
	}
}
inline void add(int op,int x,int val){for(;x<=T;x+=x&-x)c[op][x]+=val;}
inline int ask(int op,int x){int sum=0;for(;x;x-=x&-x)sum+=c[op][x];return sum;}
inline void change(int op,int l,int r,int k){
	if(l>r)return;
	l=lower_bound(u+1,u+T+1,l)-u;
	r=upper_bound(u+1,u+T+1,r)-u-1;
	add(op,l,k);add(op,r+1,-k);
}
vector<node>w[N];vector<int>dl[N];
signed main(){
	scanf("%lld%lld",&n,&m);t=log2(n+1);
	lg[0]=-1;rep(i,1,n)lg[i]=lg[i>>1]+1;
	rep(i,1,n)scanf("%lld",&a[i]),s[i+1]=s[i]+a[i];
	rep(i,1,n)scanf("%lld",&b[i]);
	st1::init();st2::init();
	rep(i,1,m)scanf("%lld%lld%lld",&q[i].s,&q[i].t,&q[i].u),o[i]=q[i].u;
	sort(o+1,o+m+1);rep(i,1,m)if(o[i]!=o[i-1])u[++T]=o[i];
	rep(i,1,m){
		int l=q[i].s,r=q[i].t-1,ed=q[i].t-1;
		while(l<=r){
			int mid=(l+r)>>1;
			if(s[q[i].t]-s[mid]<=q[i].u)ed=mid,r=mid-1;
			else l=mid+1;
		}
		int cur=st1::ask(ed,q[i].t-1);
		node now;now.u=q[i].u,now.s=i,now.t=1;
		w[q[i].s].push_back(now);
		now.s=i,now.t=-1;w[cur].push_back(now);
		ans[i]+=(s[q[i].t]-s[cur])*b[cur];
	}
	pre(i,n,1){
		while(top&&b[sta[top]]>=b[i]){
			pr[sta[top]]=i;top--;
		}
		if(top)nx[i]=sta[top];
		sta[++top]=i;
	}
	rep(i,1,n)if(!nx[i])nx[i]=n+1;
	pre(i,n,1){
		change(0,0,s[nx[i]]-s[i],b[i]);
		change(1,s[nx[i]]-s[i]+1,0x7fffffff,b[i]*(s[nx[i]]-s[i]));
		dl[pr[i]].push_back(i);
		for(int j=0;j<(int)dl[i].size();j++){
			int x=dl[i][j];
			change(0,s[x]-s[i],s[nx[x]]-s[i],-b[x]);
			change(1,s[x]-s[i],s[nx[x]]-s[i],b[x]*(s[x]-s[i]));
			change(1,s[nx[x]]-s[i]+1,0x7fffffff,-b[x]*(s[nx[x]]-s[x]));
		}
		for(int j=0;j<(int)w[i].size();j++){
			int cur=lower_bound(u+1,u+T+1,w[i][j].u)-u;
			ans[w[i][j].s]+=w[i][j].t*(w[i][j].u*ask(0,cur)+ask(1,cur));
		}
	}
	rep(i,1,m){
		if(q[i].u<a[st2::ask(q[i].s,q[i].t-1)])puts("-1");
		else printf("%lld\n",ans[i]);
	}
	return 0;
}