1.作业内容
ADT Rational{
数据对象:
D={e1,e2|e1,e2属于整数类型}
数据关系:
R={<e1,e2>|e1为有理数分子,e2为有理数分母}
基本操作:
InitRational(&T,e1,e2):构造有理数T,e1为有理数分子,e2为有理数分母
DestroyRational(&T):销毁有理数T
AddRational(T1,T2,&T3):有理数T1,T2相加,结果存入有理数T3
SubRational(T1,T2,&T3):有理数T1,T2相减,结果存入有理数T3
MulRational(T1,T2,&T3):有理数T1,T2相乘,结果存入有理数T3
DivRational(T1,T2,&T3):有理数T1,T2相除,结果存入有理数T3
int gcd(a,b):求最大公约数
}ADT Rational
2.数据结构、函数说明(截图展示你的头文件;头文件代码加入注释)
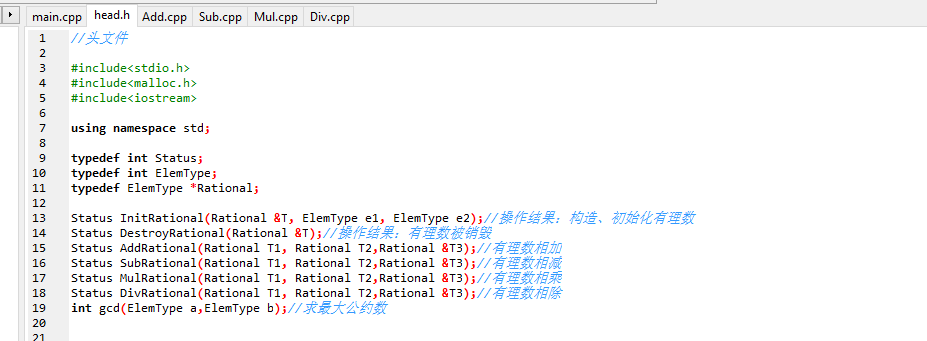
3.代码实现说明

- 做法:输入两个有理数分子、分母并构造,调用四则运算;
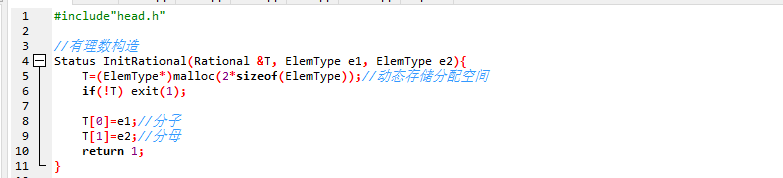
- 做法:动态分配存储空间,分别把2个变量分子、分母放入e1、e2中;

- 做法:利用辗转相除法,不断取余,直到求出最大公约数,商为0;
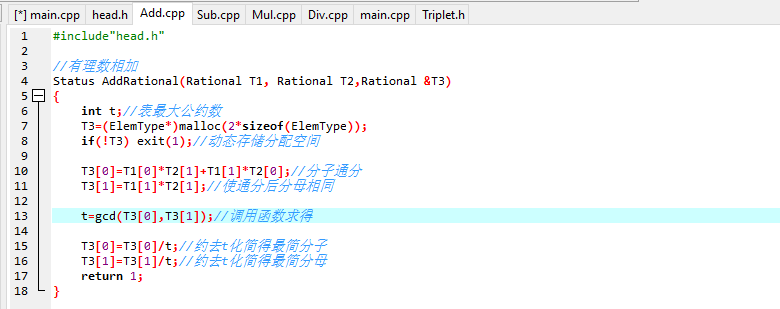
- 做法:把有理数分子、分母都通分,然后相加,调用公约数函数,约去,化成最简分数;
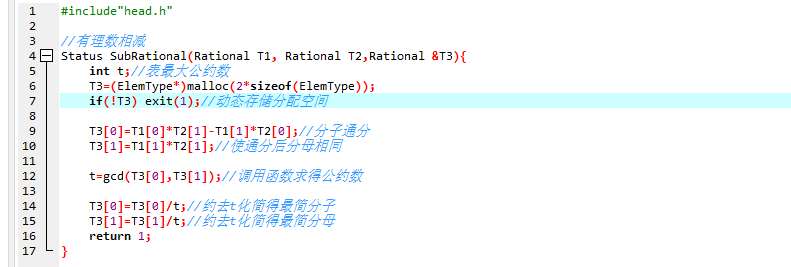
- 做法:把有理数分子、分母都通分,然后相减,调用公约数函数,约去,化成最简分数;
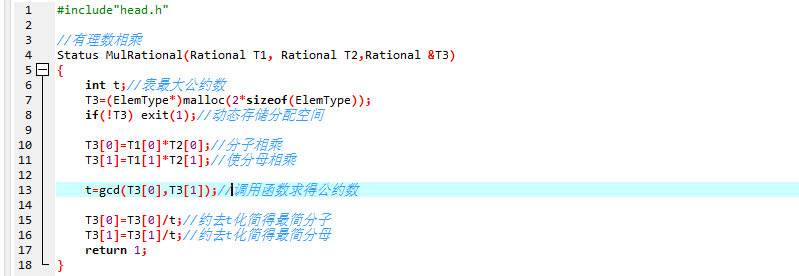
- 做法:把有理数分子、分母各自相乘,然后,调用公约数函数,约去,化成最简分数;
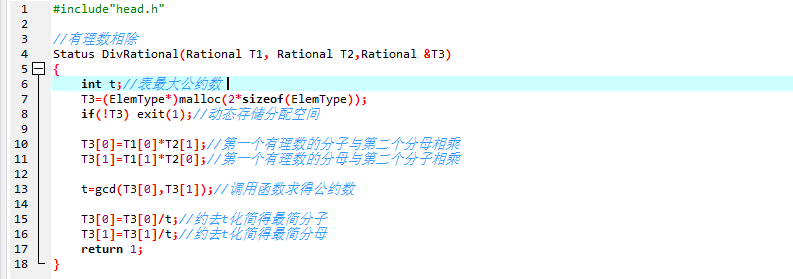
- 做法:把第一个有理数与第二个有理数的倒数之间进行相乘,然后,调用公约数函数,约去,化成最简分数;

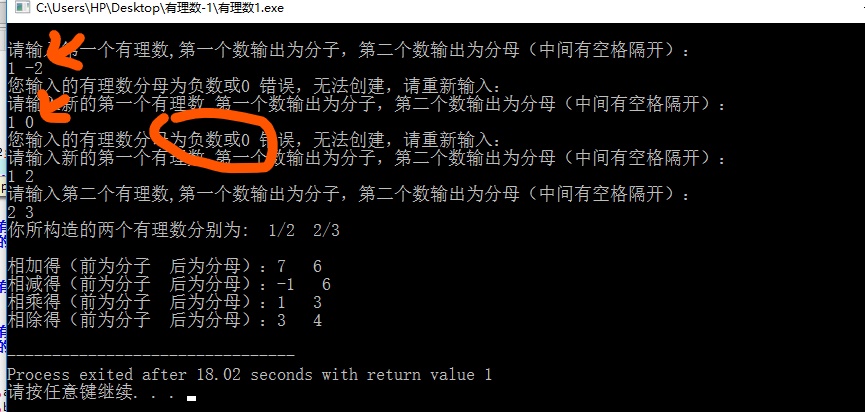
4.结果展示
- 最后功能实现和出错处理:
5.总结
通过这次作业,对数据结构及抽象数据类型的理解主要有以下几点:
- 数据结构,是对于所包含的数据对象进行实现最终结果功能的一种操作,不仅要考虑到研究的对象,还要有其对应关系,以及如何设计算法能让程序更简洁、高效的具体算法的实现;
- 抽象数据类型,仅仅只是对数据类型的一种描述,而描述是抽象的,即其使用的方法没有具体实现,只是写出总的大纲,写出每个操作做什么,而非如何做,只是一种算法;












