转载（气泡的附加压力与热力学基本方程）

       本文拟结合准静态过程假说，探究气泡附加压力与热力学基本方程的内在关联，供参考.

1. 含表面张力的热力学基本方程

   准静态过程假说中含表面张力的热力学基本方程，参见如下式（1）^[1]:

   dG=γdA_s=-SdT+Vdp+δW'                  （1）

   需明确，式（1）中并未出现体势变（-pdV）或体积功（-p_edV)项，这表明该方程与体势变或体积

功无关^[2].

   2. 拉普拉斯方程

      气泡成长过程示意图，参见如下图1.

                                    

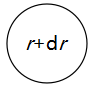
                             图1.气泡成长过程示意图

      气泡在附加压力p作用下，体积不断膨胀，最终破裂. 

      气泡成长过程，dT=0, δW' =0.

      此时式（1）可化简为：

       dG=γdA_s=Vdp                                  （2）

       对于球形气泡，A_s=4πr², V=4/3·πr³.

       则：dA_s=8πr·dr                                     (3)

       将式（3）及相关条件代入式（2）可得：

       dG=γ·8πr·dr=4/3·πr³dp                       （4）

        整理式（4）可得：dp=(6γ/r²)dr      （5）

         式（5）积分可得：

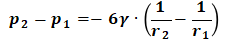            （6）

         式（6）中“p₂与p₁”分别为半径为“r₂与r₁”时，气泡所承受的附加压力. 

         同时式（6）也显示气泡半径越大，附加压力越大.

         当液面为平面时，r₁=∞，p₁=0.

         将上述数据代入式（6）可得：

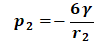                                          （7）

          整理式（7）可得：

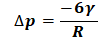                                      （8）

         式（8）中Δp代表气泡的附加压力；γ表示液体的表面张力；R代表气泡的半径.

    3.结论

       ⑴气泡成长过程，，气泡半径越大，附加压力越大；

       ⑵气泡成长过程: dG=γdA_s=Vdp;

       ⑶气泡成长过程δW' =0.

参考文献

[1]余高奇. 表面张力的热力学属性探究.http://blog.sciencenet.cn/u/yugaoqi666.科学网博客,2023,12.

[2]余高奇. 热力学第一定律研究.http://blog.sciencenet.cn/u/yugaoqi666.科学网博客,2021,8.