二叉树

第四章 树

三. 二叉树的存储结构

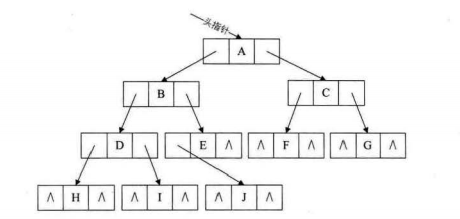
1. 二叉链表
   （1）左右孩子指针为空的，途中用^表示

   #include <stdio.h>
   #include <stdlib.h>
   typedef char TElemType ;
   #define MAXTREESIZE 1000
   typedef struct BiTnode{
   	TElemType data;
   	struct BiTnode *lchild,* rchild;
   }BiTnode,* BiTree;
   

2. 遍历二叉树
   （1）前序遍历：先根节点，在左右子树
   （2）中序遍历：先左子树，根节点，右子树
   （3）后序遍历：先左右子树，最后根节点

   /*  前序遍历 */
   void preOrderTraverse(BiTree tree){
   	if(tree == NULL)
   		return;
   	printf("%c\n", tree->data);
   	preOrderTraverse(tree->lchild);
   	preOrderTraverse(tree->rchild);
   }
   /*  中序遍历  */
   void inOrderTraverse(BiTree tree){
   	if(tree == NULL)
   		return;
   	inOrderTraverse(tree->lchild);
   	printf("%c\n", tree->data);
   	inOrderTraverse(tree->rchild);
   }
   /*  后序遍历  */
   void postOrderTraverse(BiTree tree){
   	if(tree == NULL)
   		return;
   	postOrderTraverse(tree->lchild);
   	postOrderTraverse(tree->rchild);
   	printf("%c\n", tree->data);
   }
   

（4）层次遍历：树的第一层->第二层->第n层

3. 推导遍历结果
   有一种题型是给出前续+中续或后续+中续，求后续和前序遍历
   这种题型现根据前序和后序找出根节点（第一个和最后一个打印），然后用根节点划分中序遍历为两部分，再去试

4. 建立二叉树
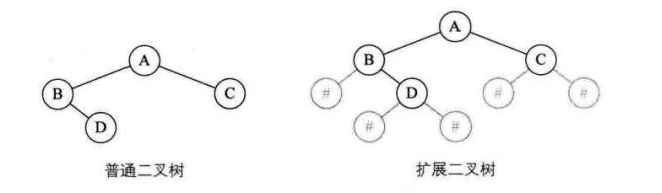
   （1）让用户输入每个二叉树节点的data值。为了确定每个节点是否有左右孩子，我们规定将二叉树中每个节点的空左右孩子指针引出一个虚节点，该虚节点有特定值"#"。使得原二叉树变成扩展二叉树。
   （2）此时，若要形成下图的二叉树，其前序遍历的序列就为AB#D##C##
   

   /*  以先序遍历的节点顺序输入  */
   void createBiTree(BiTree *tree){
           TElemType ch;
           scanf("%c",&ch);
           getchar();
           printf("%d\n",ch);
           if(ch == '#'){
                           *tree = NULL;
                           return;
           }
           *tree = (BiTree)malloc(sizeof(BiTnode));
           (*tree)->data = ch;
           createBiTree(& (*tree)->lchild);
           createBiTree(& (*tree)->rchild);
   }
   

5. 线索二叉树
   （1）普通二叉树的结点分为数据域和指针域，指针域指向左右孩子结点。但是没有左右孩子的结点，其指针域指向空，也就浪费了这个指针。
   （2）线索二叉树，对于没有左右孩子的节点，其lchild指针指向前驱结点，其rchild指针，指向后继结点。此时，加上线索的二叉链表成为线索链表。线索化的二叉树便于查找某些结点的前驱和后继结点。
   （3）为了区分指针志向的时孩子结点还是前驱后继结点，引入ltag和rtag标记。标记为0，指向左右孩子；标记为1，指向前驱后继
   （4）线索二叉树的定义

   #include <stdio.h>
   typedef char TElemType ;
   #define MAXTREESIZE 1000
   typedef enum {   // Link=0,指向孩子结点。Thread=1，指向前驱后继
       Link,Thread;
   } PointerTag;
   
   typedef struct BiThreadNode{
       TElemType data;
       struct BiThreadNode *lchild,*rchild;
       PointerTag ltag;
       PointerTag rtag;
   }BiThreadNode,*BiThrTree;
   

（5）对二叉树进行中序遍历线索化
c /* 中序遍历对二叉树中序线索化 */ BiThreadNode *pre; // 全局变量，指向刚刚访问过的节点 void inThreading(BiThreadNode *node){ if(node == NULL) return; inThreading(node->lchild); if(node->lchild == NULL){ // 没有左孩子 node->ltag = Thread; // 线索 node->lchild = pre; } if(pre->rchild == NULL){ // 前驱没有右孩子 pre->rtag = Thread; pre->rchild = node; } pre = node; inThreading(node->rchild); }

6. 树，森林转化为二叉树
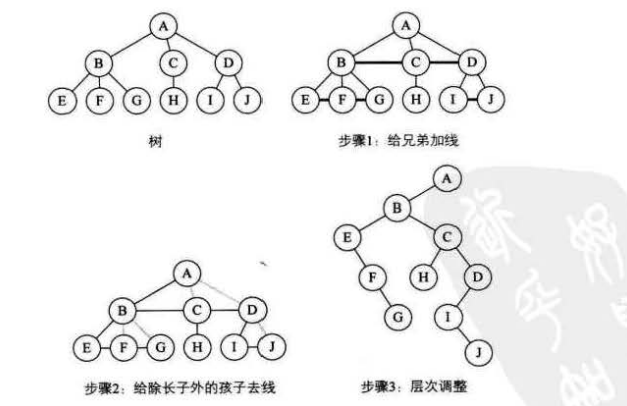
   （1）树转化为二叉树
       1）在同层所有相邻的兄弟结点之间，加上一条线
       2）只保留结点的第一个孩子结点的连线，删除其余所有孩子结点的连线
       3）此时，二叉树建立完毕，最后调整为正常的二叉树图形形式。
       
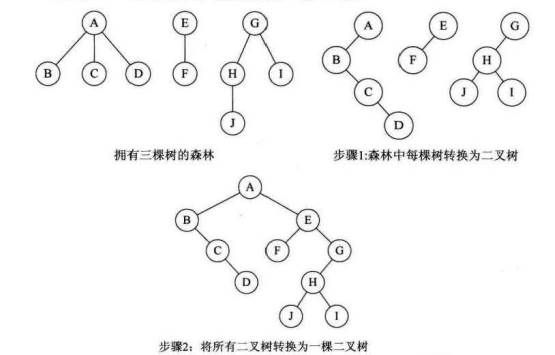
   （2）森林转化为二叉树
       1）把森林中的每个树都转换成二叉树
       2）依次把后一棵树的根节点，作为前一棵二叉树的根节点的右孩子连接上去，形成一个大的二叉树。（由树转化而成的二叉树，根节点没有右孩子）
       
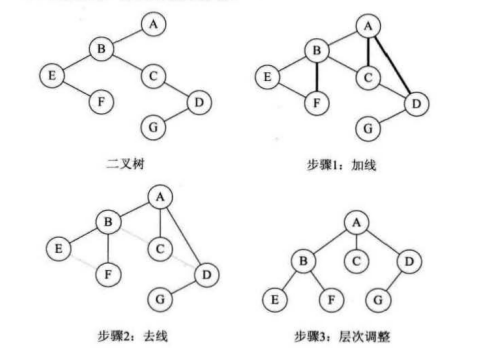
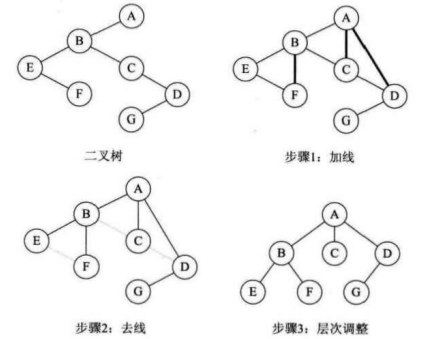
   （3）二叉树转化为树
       1）加线：把每个结点的左孩子的右孩子结点，左孩子的右孩子的右孩子结点 。。。左孩子所有右孩结点的右孩子结点与该结点连线连接
       2）去线：删除原二叉树中所有结点与其右孩子结点的连线。
       
   （4）二叉树转化为森林
       判断一棵树原来是森林还是树，只要看这个二叉树的根节点有没有右孩子即可。有右孩子，则是森林
       1）从根节点开始，把每个右孩子结点的连线断掉
       2）对形成的多个树转换成二叉树
       

7. 压缩编码的始祖：霍夫曼编码
   （1）霍夫曼树：
   霍夫曼树解决了当存在大量输入需要进行条件分支选择时，总输入的条件判断次数最少的解法。
   比如如下成绩判断代码：

   if(a>60)
       b="不及格";
   else if(a<70)
       b="及格"；
   else if(a<80)
       b="中等";
   else if(a<90)
       b="优秀"；
   

该代码粗看下没什么问题，但是输入量很大时就会有问题。发现不及格的人数非常少，中等的人最多，但是要判断成中等，需要经过是否大于60，大于70，大于80的三次判断才能出结果。如果把大于80小于90作为第一个条件判断，效率会大大提升。
（2）霍夫曼树的定义：
带权路径长度WPL最小的二叉树称为霍夫曼树。WPL=每个结点的路径长度 * 节点权值
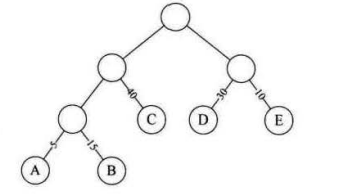WPL=53 + 153 + 402 + 302 + 10*2 = 220
（3）霍夫曼树的构建过程
选择权值最小的两个节点组成一个二叉树，该二叉树的根节点的权值为2个孩子结点权值之和，将该形成的二叉树加入备选结点。不断重复这个过程，直到点全部加入到二叉树。

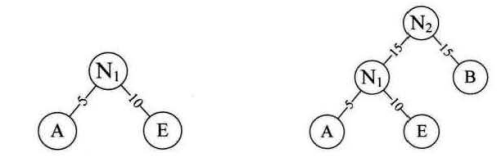
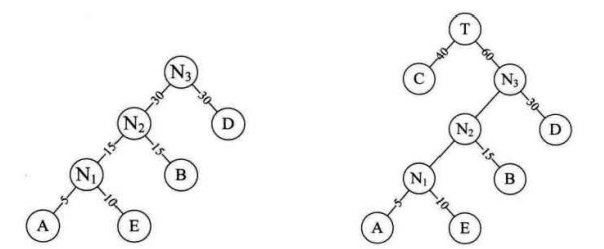
（4）霍夫曼编码
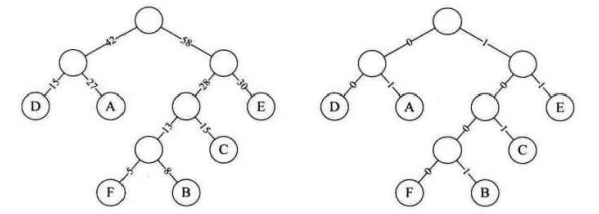
比如一段消息包含ABCDEF几个字母，进行压缩发送。再给每个字母进行01编码时，通过字母出现次数作为权值，构建霍夫曼树，形成的每个字母的编码就是霍夫曼编码。霍夫曼编码使得编码后的总码字长最小。
eg：一段报文中，A出现27次，B出现8次，C出现15次，D出现15次，E出现30次，F出现5次，进行霍夫曼编码。