数论——原根
参照篇原根博客:https://blog.csdn.net/fuyukai/article/details/50894609
1.原根定义
(1)假设一个数g对于P来说是原根,那么g^i mod P的结果两两不同,且有 1<g<P, 1<i<P,那么g可以称为是P的一个原根
简单来说,g^i mod p ≠ g^j mod p (p为素数)
(2)如果从欧拉函数的角度定义,我们可以先引进一个概念:阶
关于阶可以看这里:https://blog.csdn.net/a27038/article/details/77203892
此时给原根下定义:
此时给原根下定义:
如果 a 与 n 是互质的整数且n>0,那么当 ordna=φ(n)时,称aa为模n的原根。
有个结论:如果g是P的原根,就是g^(P-1) = 1 (mod P)当且仅当指数为P-1的时候成立.(这里P是素数).
2.如何求解:
一、枚举
从2开始枚举,然后暴力判断g^(P-1) = 1 (mod P)是否当且当指数为P-1的时候成立
而由于原根一般都不大,所以可以暴力得到.
二、讲究方法
定理:如果模m有原根,那么他一共有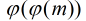
定理:如果p为素数,那么素数p一定存在原根,并且模p的原根的个数为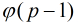
定理:假设m是正整数,a是整数,如果a模m的阶等于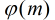
模m有原根的充要条件:m=2,4,P^a,2*P^a…….
求模素数P的原根的方法:对P-1素因子分解,即P-1=(P1^a1)(P2^a2)…..(Pk^ak)。,若恒有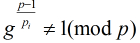
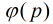
求解一个数最小原根代码:

1 #include <stdio.h> 2 #include <algorithm> 3 #include <cmath> 4 #include <iostream> 5 #include <string.h> 6 #include <cstring> 7 using namespace std; 8 const int MAX_N = 1000010; 9 typedef long long ll; 10 11 int prime_cnt, factor_cnt, p; 12 int vis[MAX_N], prime[MAX_N], factor[MAX_N]; 13 14 void GetPrime() 15 { 16 prime_cnt = 0; 17 memset(vis, 0, sizeof(vis)); 18 for(int i = 2; i < MAX_N; i++){ 19 if(!vis[i]){ 20 prime[prime_cnt++] = i; 21 for(int j = 0; j < prime_cnt && prime[j] * i < MAX_N; j++){ 22 vis[i * prime[j]] = 1; 23 if(i % prime[j] == 0) break; 24 } 25 } 26 } 27 } 28 29 void Factor(int x) 30 { 31 factor_cnt = 0; 32 int t = (int) sqrt(x + 0.5); 33 for(int i = 0; prime[i] <= t; i++){ 34 if(x % prime[i] == 0){ 35 factor[factor_cnt++] = prime[i]; 36 while(x % prime[i] == 0) x /= prime[i]; 37 } 38 } 39 if(x > 1) factor[factor_cnt++] = x; 40 } 41 42 ll quick_pow(ll n, ll m, ll mod) 43 { 44 ll res = 1, tmp = n % mod; 45 while(m){ 46 if(m & 1) res = res * tmp % mod; 47 tmp = tmp * tmp % mod; 48 m >>= 1; 49 } 50 return res; 51 } 52 53 void solve() 54 { 55 Factor(p - 1); 56 for(int g = 2; g < p; g++){ 57 bool flag = true; 58 for(int i = 0; i < factor_cnt; i++){ 59 int t = (p - 1) / factor[i]; 60 if(quick_pow((ll)g, (ll)t, (ll)p) == 1){ 61 flag = false; 62 break; 63 } 64 } 65 if(flag){ 66 cout << g << endl; 67 break; 68 } 69 } 70 } 71 72 int main() 73 { 74 GetPrime(); 75 while(cin >> p){ 76 solve(); 77 } 78 return 0; 79 }

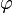 函数定理)是一个关于同余的性质。欧拉定理表明,若
函数定理)是一个关于同余的性质。欧拉定理表明,若 为正
为正 ),则
),则
 时,定义
时,定义 对模
对模 的指数
的指数 为使
为使 成立的最小的正整数
成立的最小的正整数 。由前知
。由前知 ,若
,若 ,则称
,则称

