网络流24题——最小路径覆盖问题

问题描述：

给定有向图G=(V,E)。设P 是G 的一个简单路（顶点不相交）的集合。如果V 中每个顶点恰好在P 的一条路上，则称P是G 的一个路径覆盖。P 中路径可以从V 的任何一个顶点开始，长度也是任意的，特别地，可以为0。G 的最小路径覆盖是G 的所含路径条数最少的路径覆盖。设计一个有效算法求一个有向无环图G 的最小路径覆盖。

---

 

编程任务：

对于给定的给定有向无环图G，编程找出G的一个最小路径覆盖。

---

预备知识：我看描述还是不懂最小路径覆盖是什么东西（太蒟蒻没办法），觉得网上这两张图还是很好理解的

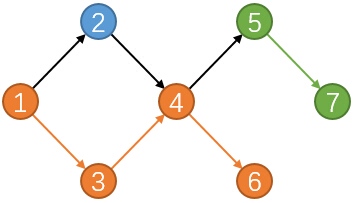
橙色为一条路径，找完后变成这样

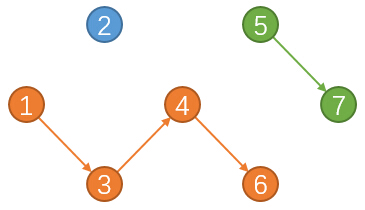
也就是说，从入度为零的点开始找路径直至找到出度为零的，每找完一条路径，把其路径上的点的所有出边入边都切断，再继续从别的入度为零的点开始，直到覆盖完所有的点，所用的路径数就是最小路径覆盖。

---

建模：把一个点变成两个点x，y。假设两个点u，v相连，建图时将u的x向v的y连一条边，源点s向所有的x连边，所有的y向汇点连边，跑一边网络流找到最大匹配，用点数n-最大匹配即为答案。

可以这么理解：如果无匹配，显然要n条路径才能覆盖所有点，两个点匹配意味着将可以把它们用一条路径覆盖，路径数就可以减1。当然，既然可以用网络流找最大匹配，二分图也可以，码量还会少点。

---

dinic最大流做法代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#define inf 0x7fffffff
using namespace std;
int n,m,cnt=1,ans,head[10001],q[10001],to[10001],h[10001];
bool mark[10001];
struct node{int to,nex,val;}e[2000001];
void ins(int u,int v,int w)
{
    cnt++;
    e[cnt].to=v;
    e[cnt].val=w;
    e[cnt].nex=head[u];
    head[u]=cnt;
}
void insert(int u,int v,int w)
{
    ins(u,v,w);
    ins(v,u,0);
}
bool bfs()
{
    memset(h,-1,sizeof(h));
    q[0]=h[0]=0;
    int l=0,r=1;int u;
    while (l<r)
    {
        u=q[l++];
        for (int i=head[u];i;i=e[i].nex)
        {
            int ne=e[i].to;
            if (h[ne]==-1&&e[i].val)
            {
                h[ne]=h[u]+1;
                q[r++]=ne;
            }
        }
    }
    if (h[8001]==-1) return 0;
    return 1;
}

int dfs(int u,int flow)
{
    int used=0,w;
    if (u==8001) return flow;
    for (int i=head[u];i;i=e[i].nex)
    {
        int ne=e[i].to;
        if (h[ne]==h[u]+1&&e[i].val)
        {
            w=flow-used;
            w=dfs(ne,min(w,e[i].val));
            e[i].val-=w,e[i^1].val+=w;
            used+=w;
            if (w!=0)
            {
                to[u]=ne;
                if (e[i].to-n>0) mark[ne-n]=1;
            }
            if (used==flow) return flow;
        }
    }
    if (!used) h[u]=-1;
    return used;
}
void dinic(){while(bfs())ans-=dfs(0,inf);}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
       {
          int u,v;
          scanf("%d%d",&u,&v);
          insert(u,v+n,inf);
       }
    for(int i=1;i<=n;i++)insert(0,i,1);
    for(int i=1;i<=n;i++)insert(i+n,8001,1);
    ans=n;
    dinic();
    for(int i=1;i<=n;i++)
    {
        if(mark[i])continue;
        printf("%d",i);
        int k=i;
        while(to[k])
        {
            printf(" %d",to[k]-n);
            k=to[k]-n;
        }
        printf("\n");
    }
    printf("%d",ans);
    return 0;       
}