POJ 1006 ( 中国剩余定理 )
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 112904 | Accepted: 35320 |
Description
Input
Output
Sample Input
0 0 0 0 0 0 0 100 5 20 34 325 4 5 6 7 283 102 23 320 203 301 203 40 -1 -1 -1 -1
Sample Output
Case 1: the next triple peak occurs in 21252 days. Case 2: the next triple peak occurs in 21152 days. Case 3: the next triple peak occurs in 19575 days. Case 4: the next triple peak occurs in 16994 days. Case 5: the next triple peak occurs in 8910 days. Case 6: the next triple peak occurs in 10789 days.
代码如下:
#include<stdio.h>
#include<math.h>
#define LL long long
LL MM[10], NN[10], m[10]={23, 28, 33}, x, y;
int extend_gcd(LL a, LL b, LL &x, LL &y)
{
if(b==0) { x=1; y=0; return a;}
LL d = extend_gcd(b, a%b, x, y);
LL t = x;
x = y;
y = t-a/b*y;
return d;
}
int main()
{
int p, e, i ,d, j, k=0;
LL M, X, dd;
while(~scanf("%d%d%d%d", &p, &e, &i, &d))
{
if(p==-1 && e==-1 && i==-1 && d==-1)
break;
M = m[0]*m[1]*m[2];
for(j=0; j<3; j++)
MM[j] = M/m[j];
for(j=0; j<3; j++)
{
dd = extend_gcd(MM[j], m[j], x, y);
x = x*(1/dd);
x = (x%m[j]+m[j])%m[j];
NN[j] = x;
}
X = (MM[0]*NN[0]*p + MM[1]*NN[1]*e + MM[2]*NN[2]*i)% M;
if(X==21252 && d==21252)
printf("Case %d: the next triple peak occurs in 21252 days.\n", ++k);
else if(X==0 && d!=21252)
printf("Case %d: the next triple peak occurs in %d days.\n", ++k, 21252-d);
else printf("Case %d: the next triple peak occurs in %lld days.\n", ++k, (X+21252-d)%21252);
}
return 0;
}
此题注意判断当X==0 的情况, else if(X==0 && d!=21252) 直接输出 21252-d 即可。
而当X==21252 && d==21252时,直接输出 21252 即可。
其他情况直接输出 (X+21252-d)%21252 这里是为保证为正数。
中国剩余定理:
————————————————————————————————————————————————————————————————————————————
形式描述
用现代数学的语言来说明的话,中国剩余定理给出了以下的一元线性同余方程组:
有解的判定条件,并用构造法给出了在有解情况下解的具体形式。
中国剩余定理说明:假设整数m1,
m2, ... , mn两两互质,则对任意的整数:a1,
a2, ... , an,方程组 有解,并且通解可以用如下方式构造得到:
有解,并且通解可以用如下方式构造得到:
- 设
![M = m_1 \times m_2 \times \cdots \times m_n = \prod_{i=1}^n m_i]() 是整数m1,
m2, ... , mn的乘积,并设
是整数m1,
m2, ... , mn的乘积,并设![M_i = M/m_i, \; \; \forall i \in \{1, 2, \cdots , n\}]() 是除了mi以外的n
- 1个整数的乘积。
是除了mi以外的n
- 1个整数的乘积。 - 设
![t_i = M_i^{-1}]() 为
为![M_i]() 模
模![m_i]() 的数论倒数:
的数论倒数:![t_i M_i \equiv 1 \pmod {m_i}, \; \; \forall i \in \{1, 2, \cdots , n\}.]()
- 方程组
![(S)]() 的通解形式为:
的通解形式为:![x = a_1 t_1 M_1 + a_2 t_2 M_2 + \cdots + a_n t_n M_n + k M= k M + \sum_{i=1}^n a_i t_i M_i, \quad k \in \mathbb{Z}.]() 在模
在模![M]() 的意义下,方程组
的意义下,方程组![(S)]() 只有一个解:
只有一个解:![x = \sum_{i=1}^n a_i t_i M_i.]()
————————————————————————————————————————————————————————————————————————————
此题中的变量对应公式中: a1 = p, m1 = 23; Mi ~~MM[ j ]; ti ~~NN[ j ];
a2 = e, m2 = 28;
a3 = i, m3 = 33;
此题运用中国剩余定理,然后在求 ti 的时候运用拓展欧几里得即可。



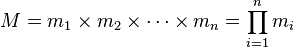 是整数
是整数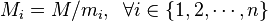 是除了
是除了 为
为 模
模 的数论倒数:
的数论倒数:
 在模
在模 的意义下,方程组
的意义下,方程组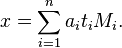

 浙公网安备 33010602011771号
浙公网安备 33010602011771号