斜率优化入门小记

斜率优化入门小记

本文仅作为我入门斜率优化 dp 的学习记录和总结。

引入

我们知道，当一个 1D/1D 的动态规划问题可以将方程写作形如 $dp(i)=\min/\max\{dp(j)+a_i+b_j\}$ 的形式时，可以使用单调队列进行优化，将时间复杂度做到转移均摊 $\mathcal O(1)$ 的时间复杂度。

实际问题中，部分 1D/1D 动态规划的转移方程写作 $dp(i)=\min/\max\{dp(j)+a_i\times b_j+c_i+d_j\}$ 的形式。此时直接计算是 $\mathcal O(n^2)$ 的。但是它仍具有很强的结构性，因此借助数学知识，我们仍然可以大幅优化其转移的时间复杂度。

斜率优化

以下内容可能较为冗长，可以选择性略过一些基础步骤。

I. 转化方程

假设当前的方程形式是 $dp(i)=\min\{dp(j)+a_i\times b_j+c_i+d_j\}$（$\max$ 的情况类似，学会了以后不难自行推导），我们先将 $\min$ 去掉，变为 $dp(i)=dp(j)+a_i\times b_j+c_i+d_j$。

考虑将原式分成三部分，方便处理：

• 只含 $i$ 的项。
• 只含 $j$ 的项。
• 包含 $i,j$ 的项。

现在的形式：$dp(i)=(dp(j)+d_j)+c_i+(a_i\times b_j)$。

II. 凸包

用数形结合的思想理解凸包会较为容易。先从代数层面说起。

考虑转移的两个决策点 $j_1,j_2$，不妨设 $j_1\lt j_2$，若 $j_2$ 优于 $j_1$，则有：

$$\qquad dp(j_2)+d_{j_2}+c_i+(a_i\times b_{j_2})\le dp(j_1)+d_{j_1}+c_i+(a_i\times b_{j_1})\\ \qquad \therefore a_i\times (b_{j_2}-b_{j_1})\le dp(j_1)+d_{j_1}-(dp(j_2)+d_{j_2})$$

记 $val(j)=dp_j+d_j$，则：

$$\qquad a_i\times (b_{j_2}-b_{j_1})\le val(j_1)-val(j_2)\\ \qquad -a_i\ge \frac{val(j_1)-val(j_2)}{b_{j_1}-b_{j_2}}$$

发现右边的式子形式很熟悉，将点 $j$ 的坐标视为 $(b_j,val(j))$，那么这个式子就代表着 $j_1,j_2$ 两点间的斜率。

换言之，当前决策点 $j_2$ 优于 $j_1$，当且仅当 $j_1,j_2$ 两点间的斜率 $\le -a_i$。反之，$j_1$ 优于 $j_2$。

下面借助数形结合的思想直观地观察，考虑下图这种情况：

图源：https://www.cnblogs.com/Xing-Ling/p/11210179.html

将 $-a_i$ 视作一条直线画在图上，记斜率为 $k_0$，直观地表现出来，显然只有三种情况：

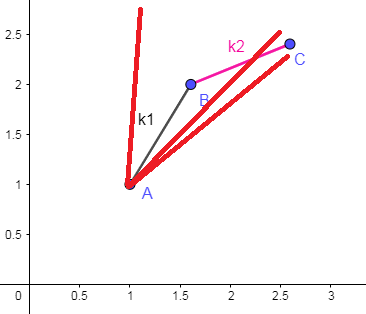
• $k_0\ge k_1\gt k_2$，则 $C$ 优于 $B$ 优于 $A$。
• $k_1\gt k_0\gt k_2$，则 $C$ 优于 $B$，且 $A$ 优于 $B$。
• $k_1\gt k_2\ge k_0$，则 $A$ 优于 $B$ 优于 $C$。

综上，无论哪种情况，$B$ 都不会成为最优决策点，直接将其移除决策点集合。

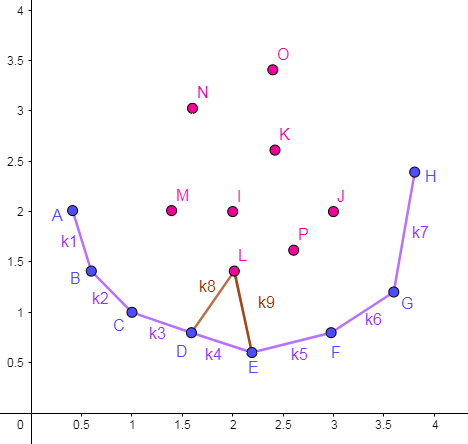
事实上，上文图片中的结构叫作上凸包，其中的若干条直线斜率单调递减，在原方程取 $\min$ 时，我们不断删去这一结构，最后会得到下面这一斜率单调递增的结构，称为下凸包：

图源：https://www.cnblogs.com/Xing-Ling/p/11210179.html

回顾我们最初提出的，当 $j_1,j_2$ 间斜率 $\le -a_i$，$j_2$ 优于 $j_1$。

根据上述推导，最优决策点会在这个下凸包中产生。而一定存在一点 $j$，使得其与左邻点间斜率 $\le -a_i$，与右邻点间斜率 $\gt -a_i$，那么 $j$ 就是最优决策点。

又因下凸包点集的斜率单增，所以我们二分查找出第一个斜率 $\gt -a_i$ 的线段，它的左端点即为最优决策点。

相似地，我们也可以推导出取 $\max$ 的维护方式，或是将原式贡献取反，做取 $\min$ 的计算，最后再将答案取反。

III. 线性规划

在上述过程中，我们主要使用代数思想推导，也使用了一定的图形辅助理解。接下来将用图形的角度去理解斜率优化。

图源：https://www.cnblogs.com/Xing-Ling/p/11210179.html

将原问题转化一下，可以抽象出以下模型：

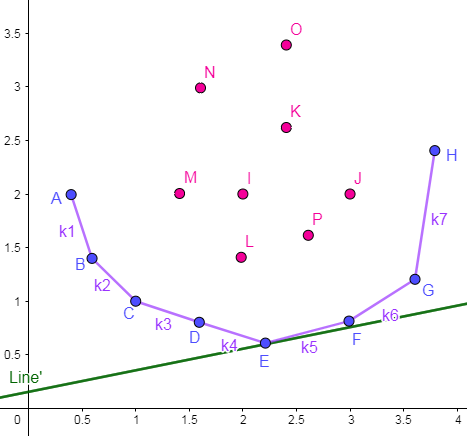
给定点集 $\{(x,y)\}$ 和斜率 $k$，在点集中选择一点 $(x,y)$，使得满足条件 $y=kx+b$ 的截距 $b$ 最小化。

事实上，这就是线性规划问题。

运用 我还没学过 的知识，可以得到，上图 $E$ 即为最优决策点。

从几何角度可以帮助我们更直观地认识学习这一问题。尤其是在考虑单调性时，它远比代数法清晰易懂。

优化转移

斜率优化 DP 主要是借助其良好的单调性。

我们分情况讨论。下文横坐标指的是加入凸包的点的横坐标。

I. 斜率单增，横坐标单增

在一些问题中，我们会遇到斜率随着 $i$ 增大而单调递增的情形。这时我们借助单调队列，将凸包中前面斜率 $\le$ 当前斜率的部分直接移除，可以做到 $\mathcal O(n)$ 的时间复杂度。

II. 斜率不单增，横坐标单增

大部分情况下，斜率并不单增。这时我们就要采用上面提到过的二分法解决问题。时间复杂度 $\mathcal O(n\log n)$。

III. 斜率和横坐标均不单增

这本质上是个偏序问题。所以可以用 CDQ 分治维护，辅以单调队列+二分查找。当然也可以平衡树或李超线段树。

例题

代码注意一个问题：如果加入的一条线段两端点横坐标相等，无法计算斜率，需要特判并返回 inf/-inf。

[HNOI2008] 玩具装箱

令 $s_i=\sum\limits_{j=1}^i c_j+1,L\gets L+1$，则：

$$f_i=\min_{j\in [0,i)}\{f_j+(s_i-s_j-L)\}\\ \\ \to f_j+{s_j^2}=2(s_i-L)\times s_j+f_i-(s_i-L)^2$$

斜率和横坐标均单增，$\mathcal O(n)$ 维护即可。

[APIO2014] 序列分割

一个自然的想法是，分割并不容易考虑，将其视为 $k+1$ 段合并，显然与原问题等价。

顺着这个思路，注意到合并的顺序并没有影响，因为不同段之间的两数必然会产生一次贡献。

将其带回原问题，发现仍然成立。

设 $f_{i,k}$ 表示前 $i$ 段分割 $k$ 次的最小答案。

则：

$$f_{i,k}=\min\{f_{j,k-1}+s_j\times (s_i-s_j)\}$$

斜率优化，顺便记一下决策点，递归输出方案即可。

时间复杂度 $\mathcal O(nk)$。

[P6047] 丝之割

本题引入了一个斜率优化中比较有用的方法论：去除无用物品。

发现直接做并不好做，考虑寻找性质。

观察到，若两条弦 $(u_i,v_i),(u_j,v_j)$ 满足 $u_i\lt u_j,v_i\gt v_j$，那么显然 $j$ 是不需要的，因为弦 $i$ 「包含」弦 $j$，那么割掉弦 $i$ 时顺便就割掉了弦 $j$，这样显然不劣。

由此，将有用的弦筛出，按 $u_i$ 排序，那么 $v_i$ 也递增。并且一条连线割掉的弦是一段区间的形式。也可以通过处理 $a,b$ 的 前 / 后缀最大值，快速得到割一段弦的代价。

由于贡献是乘积的形式，斜率优化一下即可。

时间复杂度 $\mathcal O(n)$。

[USACO08 March Gold] Land Acquisition

同上题几乎一样的套路。从偏序角度考虑筛除无用物品。

[CEOI2017] Building Bridges

仍然是套路的斜率优化，不多赘述。

发现斜率和决策点横坐标均不递增，斜率可以用二分处理，但决策点不递增就比较麻烦。

考虑从偏序的角度出发，用 CDQ 分治维护，消除决策点不递增的问题。

注意：在 CDQ 维护 dp 时，正确的分治顺序应是 solve(l,mid);calculate;solve(mid+1,r)，因为 $[l,mid]$ 会影响 $[mid+1,r]$ 内部的转移。

Reference

https://www.cnblogs.com/Xing-Ling/p/11210179.html

https://www.luogu.com.cn/blog/ningago-lsh/xie-lv-you-hua-dp

https://www.cnblogs.com/alex-wei/p/DP_optimization_method_II.html

《算法竞赛进阶指南》 0x5A 斜率优化