【洛谷P3369】普通平衡树——Splay学习笔记(一)
二叉搜索树(二叉排序树)
概念:一棵树,若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉搜索树(baidu百科)。
就是一棵二叉树,所有的节点都满足:左子树内每个的点的值比当前点值小,右子树内每个的点的值比当前点值大
如下图
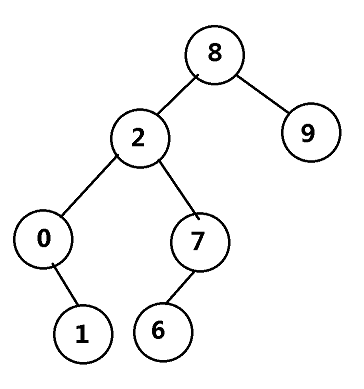
我们只需在树上中序遍历就会得到一个上升的权值序列
我们可以在二叉搜索树上干很多事情,比如插入某个值,查询第k大值,查询某个数的排名等,显然单次操作最坏复杂度为树的深度,如果树呈链状,它的复杂度就会爆炸
这时我们就要想办法保证二叉树的深度不会很大,最好是\(log\)级别的
平衡树
概念:一棵树,它是一棵空树或它的左右两个子树的高度差的绝对值不超过\(1\),并且左右两个子树都是一棵平衡二叉树(baidu百科)
不用管上面在BB啥,大概就是一棵深度为\(log\)(节点数)的二叉搜索树
平衡树有很多维护方式,这里介绍的是\(Splay\)
\(Splay\)
变量
维护一棵Splay,最基础的变量有:
root //根的编号
ch[N][2] //每个结点的两个儿子
f[N] //每个结点的父亲
cnt[N] //相同权值的点会被插入到同一个结点上,这里维护当前权值的结点上的点的个数
val[N] //每个结点的权值
size[N] //每个子树的大小
题目保证权值不同时 cnt数组就没有用了
有时候 val、size数组也不需要开
旋转
\(Splay\) 最核心的操作就是旋转
旋转就是把一个点搞到它父亲的位置,同时要保持二叉搜索树的性质,如下图

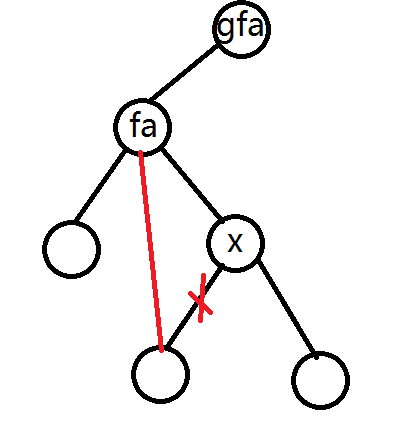
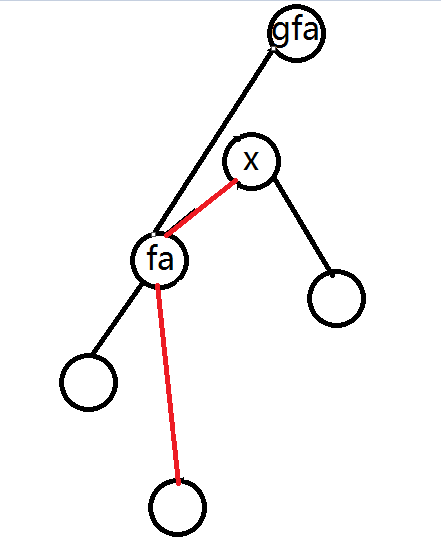
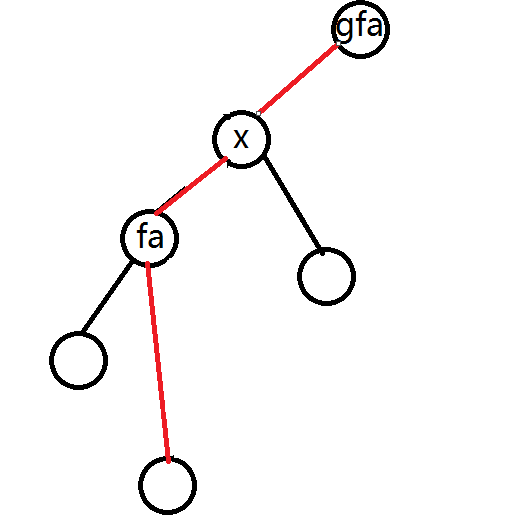
代码:
inline int get_w(int x){ //判断是x是f[x]的左儿子还是右儿子
return ch[f[x]][1]==x; //左儿子return 0,右儿子return 1
}
inline void push_up(int x){ //维护size
if(x) size[x]=size[ch[x][0]]+size[ch[x][1]]+cnt[x];
}
inline void rotate(int x){
int fa=f[x],gfa=f[f[x]],w=get_w(x);
ch[fa][w]=ch[x][w^1]; f[ch[fa][w]]=fa; //fa 与 x的儿子 的关系
ch[x][w^1]=fa; f[fa]=x; //fa 与 x 的关系
f[x]=gfa; if(gfa) ch[gfa][ch[gfa][1]==fa]=x; //x 与gfa的关系
push_up(fa); push_up(x); //fa在x的下面,先push_up(fa)
}
\(splay\) 操作
即不断地旋转一个结点,把它转到根,以方便对它操作
如下图
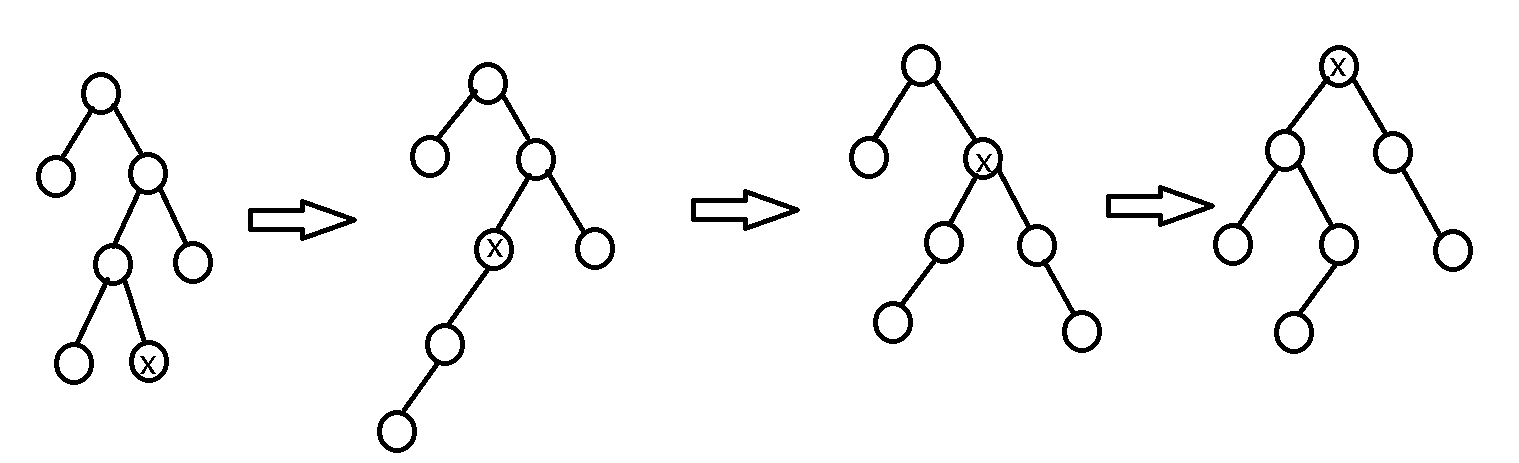
虽然它的深度没有变化我们成功把x搞到了根的位置
但是如果是一个这种形状:
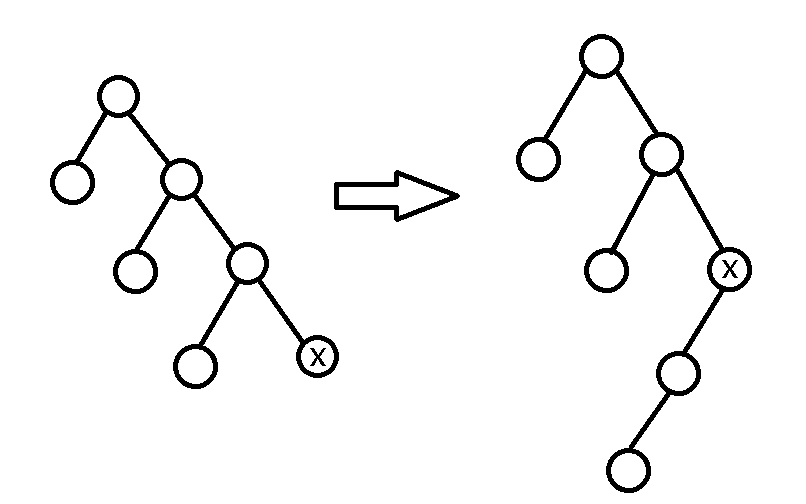
它就会非常丑
如果在\(x\)、\(fa\)、\(gfa\)在一条线上时,旋转\(fa\)就比较好看了
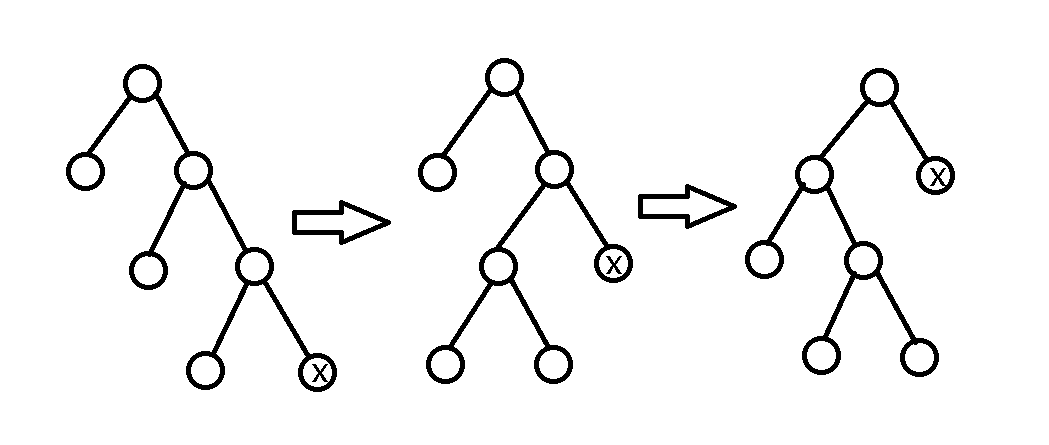
然而这里\(x\)转到根上最后深度还是会变大。。这个例子不是很好。。表在意这些细节
总之这么写就对了
inline void Splay(int x){
for(int fa;fa=f[x];rotate(x))
if(f[fa]) rotate(get_w(x)==get_w(fa)?fa:x);
root=x;
}
剩下的操作就比较好理解了
\(insert\)
插入一个点,如果\(Splay\)中有相同权值的结点,最就会在这个结点上\(cnt+1\);
如果没有相同权值的结点,就会插入到一个叶子结点上
具体看代码:
void insert(int x){
if(!root){ //Splay为空,直接设为根
val[root=++Size]=x;
size[Size]=cnt[Size]=1;
return;
}
int now=root,fa=0;
while(1){
if(val[now]==x){ //权值相同,直接++cnt[now]
++cnt[now]; push_up(now);
push_up(fa); Splay(now); //最后把now splay到根是因为插入x后,从根到now的路径上的结点size都需要更新
return;
}
fa=now;now=ch[now][x>val[now]]; //根据权值判断向左儿子/右儿子走
if(!now){ //到达叶子结点
f[++Size]=fa;val[Size]=x;
size[Size]=cnt[Size]=1;
ch[fa][val[fa]<x]=Size;
push_up(fa);Splay(Size); //Splay(Size) 和上面一样
return;
}
}
}
\(find\_num\)
查找\(Splay\)中\(rank=x\)的\(num\)
int find_num(int x){
if(!root) return 0;
int now=root;
while(1){
if(x<=size[ch[now][0]]) now=ch[now][0]; //左子树的大小等于x或者比x大,那么rank为x的数一定在左子树中
else{
int temp=size[ch[now][0]]+cnt[now];
if(x<=temp) return val[now]; //左子树的size+cnt[now]>=x,rank为x的点在now上
x-=temp; now=ch[now][1]; //rank为x的点在右子树中,在右子树中rank为x-temp
}
}
}
\(find\_rank\)
查找\(Splay\)中\(val=x\)的点的\(rank\)
int find_rank(int x){
if(!root) return 0;
int now=root,ans=0;
while(1){
if(x<val[now]) now=ch[now][0]; //val=x的点在左子树中
else{
ans+=size[ch[now][0]]; //不在左子树中,比左子树的所有结点权值都大,rank加上左子树的大小
if(x==val[now]){
Splay(now); return ans+1; //now的权值就是x,返回rank,Splay(now)是为了方便下面的del操作
}
ans+=cnt[now],now=ch[now][1]; //往右子树找
}
}
}
\(find\_pre/suf\)
查找\(root\)的前驱结点
显然\(root\)的前驱结点就是\(root\)的左子树中权值最大的点
后缀结点同理
inline int find_pre(){
int now=ch[root][0];
while(ch[now][1]) now=ch[now][1];
return now;
}
inline int find_suf(){
int now=ch[root][1];
while(ch[now][0]) now=ch[now][0];
return now;
}
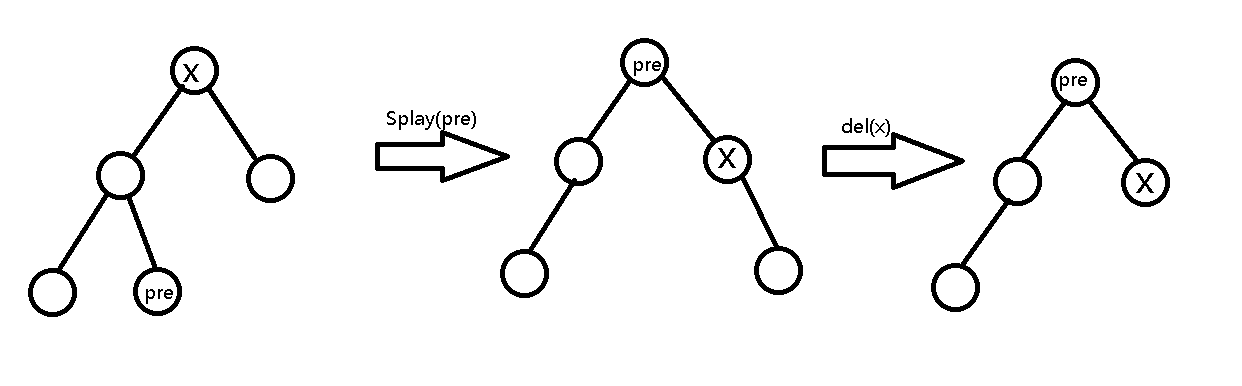
\(del\)
删除一个权值为\(x\)的点
流程:
先把权值为\(x\)的点\(splay\)到\(root\),方便操作
若\(cnt>1\),直接\(--cnt\)
否则
若左儿子为空,直接把右儿子当做根即可
若右儿子为空,同理
否则
找到\(root\)的前驱,\(splay\)到根,
原先的\(root\)一定成了新\(root\)的右儿子,且原\(root\)没有左儿子
新\(root\)、原\(root\)、原\(root\)的右儿子构成一条链的结构,用类似于链表删除操作即可删除原\(root\)
void del(int x){
find_rank(x); //找到权值为x的点并把它旋转到root
if(cnt[root]>1){
cnt[root]--; push_up(root);
return;
}
if(!ch[root][0]*ch[root][1]){
root=ch[root][0]+ch[root][1];
f[root]=0; return;
}
Splay(find_pre());
ch[root][1]=ch[ch[root][1]][1]; //删除原root
f[ch[root][1]]=root;push_up(root);
}
完整代码
#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN=100010;
inline int read(){
int x=0,f=1; char c=getchar();
while(c<'0'){if(c=='-')f=-1;c=getchar();}
while(c>='0')x=(x<<3)+(x<<1)+c-'0',c=getchar();
return x*f;
}
int n,root,Size;
int ch[MAXN][2],f[MAXN],size[MAXN],cnt[MAXN],val[MAXN];
inline int get_w(int x){
return ch[f[x]][1]==x;
}
inline void push_up(int x){
if(x) size[x]=size[ch[x][0]]+size[ch[x][1]]+cnt[x];
}
inline void rotate(int x){
int fa=f[x],gfa=f[f[x]],w=get_w(x);
ch[fa][w]=ch[x][w^1]; f[ch[fa][w]]=fa;
f[fa]=x; ch[x][w^1]=fa; f[x]=gfa;
if(gfa) ch[gfa][ch[gfa][1]==fa]=x;
push_up(x); push_up(fa);
}
inline void Splay(int x){
for(int fa;fa=f[x];rotate(x))
if(f[fa]) rotate(get_w(x)==get_w(fa)?fa:x);
root=x;
}
void insert(int x){
if(!root){
val[root=++Size]=x;
size[Size]=cnt[Size]=1;
return;
}
int now=root,fa=0;
while(1){
if(val[now]==x){
++cnt[now]; push_up(now);
push_up(fa); Splay(now);
return;
}
fa=now;now=ch[now][x>val[now]];
if(!now){
f[++Size]=fa;val[Size]=x;
size[Size]=cnt[Size]=1;
ch[fa][val[fa]<x]=Size;
push_up(fa);Splay(Size);
return;
}
}
}
int find_num(int x){
if(!root) return 0;
int now=root;
while(1){
if(x<=size[ch[now][0]]) now=ch[now][0];
else{
int temp=size[ch[now][0]]+cnt[now];
if(x<=temp) return val[now];
x-=temp; now=ch[now][1];
}
}
}
int find_rank(int x){
if(!root) return 0;
int now=root,ans=0;
while(1){
if(x<val[now]) now=ch[now][0];
else{
ans+=size[ch[now][0]];
if(x==val[now]){
Splay(now); return ans+1;
}
ans+=cnt[now],now=ch[now][1];
}
}
}
inline int find_pre(){
int now=ch[root][0];
while(ch[now][1]) now=ch[now][1];
return now;
}
inline int find_suf(){
int now=ch[root][1];
while(ch[now][0]) now=ch[now][0];
return now;
}
void del(int x){
find_rank(x);
if(cnt[root]>1){
cnt[root]--; push_up(root);
return;
}
if(!ch[root][0]*ch[root][1]){
root=ch[root][0]+ch[root][1];
f[root]=0; return;
}
Splay(find_pre());
ch[root][1]=ch[ch[root][1]][1];
f[ch[root][1]]=root;push_up(root);
}
int main()
{
n=read();
int opt,x;
while(n--){
opt=read(); x=read();
switch(opt){
case 1: insert(x); break;
case 2: del(x); break;
case 3: printf("%d\n",find_rank(x)); break;
case 4: printf("%d\n",find_num(x)); break;
case 5: insert(x);printf("%d\n",val[find_pre()]);del(x); break;
case 6: insert(x);printf("%d\n",val[find_suf()]);del(x); break;
}
}
return 0;
}

