统计分析
''' 【课程1.4】 统计分析 统计指标对定量数据进行统计描述,常从集中趋势和离中趋势两个方面进行分析 集中趋势度量 / 离中趋势度量 '''
import numpy as np import pandas as pd import matplotlib.pyplot as plt % matplotlib inline
# 1、集中趋势度量 # 指一组数据向某一中心靠拢的倾向,核心在于寻找数据的代表值或中心值 —— 统计平均数 # 算数平均数、位置平均数 # (1)算数平均数 data = pd.DataFrame({'value':np.random.randint(100,120,100), 'f':np.random.rand(100)}) data['f'] = data['f'] / data['f'].sum() # f为权重,这里将f列设置成总和为1的权重占比 print(data.head()) print('------') # 创建数据 mean = data['value'].mean() print('简单算数平均值为:%.2f' % mean) # 简单算数平均值 = 总和 / 样本数量 (不涉及权重) mean_w = (data['value'] * data['f']).sum() / data['f'].sum() print('加权算数平均值为:%.2f' % mean_w) # 加权算数平均值 = (x1f1 + x2f2 + ... + xnfn) / (f1 + f2 + ... + fn)
输出:
f value 0 0.006347 109 1 0.011855 111 2 0.003533 113 3 0.001222 116 4 0.018974 109 ------ 简单算数平均值为:109.27 加权算数平均值为:108.46
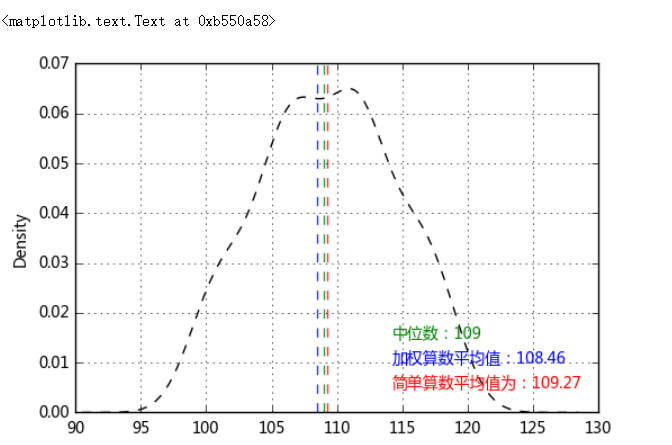
# 1、集中趋势度量 # (2)位置平均数 m = data['value'].mode() print('众数为',m.tolist()) # 众数是一组数据中出现次数最多的数,这里可能返回多个值 med = data['value'].median() print('中位数为%i' % med) # 中位数指将总体各单位标志按照大小顺序排列后,中间位置的数字 data['value'].plot(kind = 'kde',style = '--k',grid = True) # 密度曲线 plt.axvline(mean,hold=None,color='r',linestyle="--",alpha=0.8) plt.text(mean + 5,0.005,'简单算数平均值为:%.2f' % mean, color = 'r') # 简单算数平均值 plt.axvline(mean_w,hold=None,color='b',linestyle="--",alpha=0.8) plt.text(mean + 5,0.01,'加权算数平均值:%.2f' % mean_w, color = 'b') # 加权算数平均值 plt.axvline(med,hold=None,color='g',linestyle="--",alpha=0.8) plt.text(mean + 5,0.015,'中位数:%i' % med, color = 'g') # 中位数 # **这里三个数text显示的横坐标一致,目的是图示效果不拥挤
输出:
众数为 [112] 中位数为109
# 2、离中趋势度量 # 指一组数据中各数据以不同程度的距离偏离中心的趋势 # 极差与分位差、方差与标准差、离散系数 data = pd.DataFrame({'A_sale':np.random.rand(30)*1000, 'B_sale':np.random.rand(30)*1000}, index = pd.period_range('20170601','20170630')) print(data.head()) print('------') # 创建数据 # A/B销售额量级在同一水平
输出:
A_sale B_sale 2017-06-01 794.068980 531.142147 2017-06-02 99.239344 724.638103 2017-06-03 337.092146 423.990829 2017-06-04 609.858618 738.671698 2017-06-05 900.874106 525.249483 ------
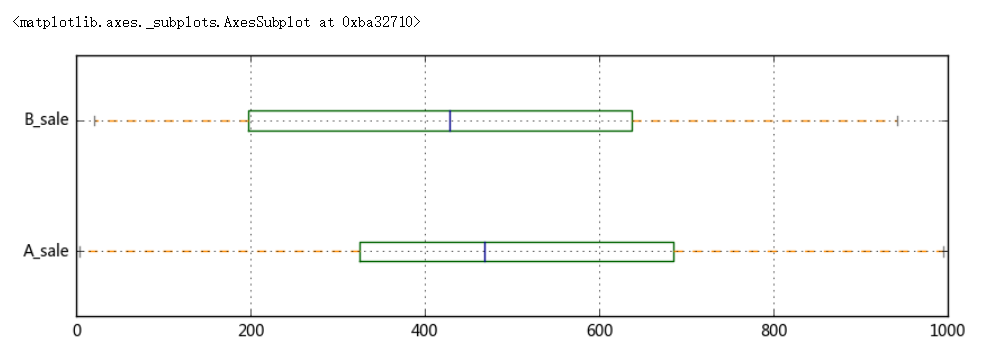
# 2、离中趋势度量 # (1)极差、分位差 data = pd.DataFrame({'A_sale':np.random.rand(30)*1000, 'B_sale':np.random.rand(30)*1000}, index = pd.period_range('20170601','20170630')) print(data.head()) print('------') # 创建数据 # A/B销售额量级在同一水平 a_r = data['A_sale'].max() - data['A_sale'].min() b_r = data['B_sale'].max() - data['B_sale'].min() print('A销售额的极差为:%.2f, B销售额的极差为:%.2f' % (a_r,b_r)) print('------') # 极差 # 没有考虑中间变量的变动,测定离中趋势不稳定 sta = data['A_sale'].describe() stb = data['B_sale'].describe() #print(sta) a_iqr = sta.loc['75%'] - sta.loc['25%'] b_iqr = stb.loc['75%'] - stb.loc['25%'] print('A销售额的分位差为:%.2f, B销售额的分位差为:%.2f' % (a_iqr,b_iqr)) print('------') # 分位差 color = dict(boxes='DarkGreen', whiskers='DarkOrange', medians='DarkBlue', caps='Gray') data.plot.box(vert=False,grid = True,color = color,figsize = (10,3)) # 箱型图
输出:
A_sale B_sale 2017-06-01 994.808396 128.929773 2017-06-02 708.276945 670.378958 2017-06-03 386.549297 334.349566 2017-06-04 478.059490 381.773828 2017-06-05 612.560799 475.183995 ------ A销售额的极差为:990.78, B销售额的极差为:921.67 ------ A销售额的分位差为:358.99, B销售额的分位差为:439.30 ------
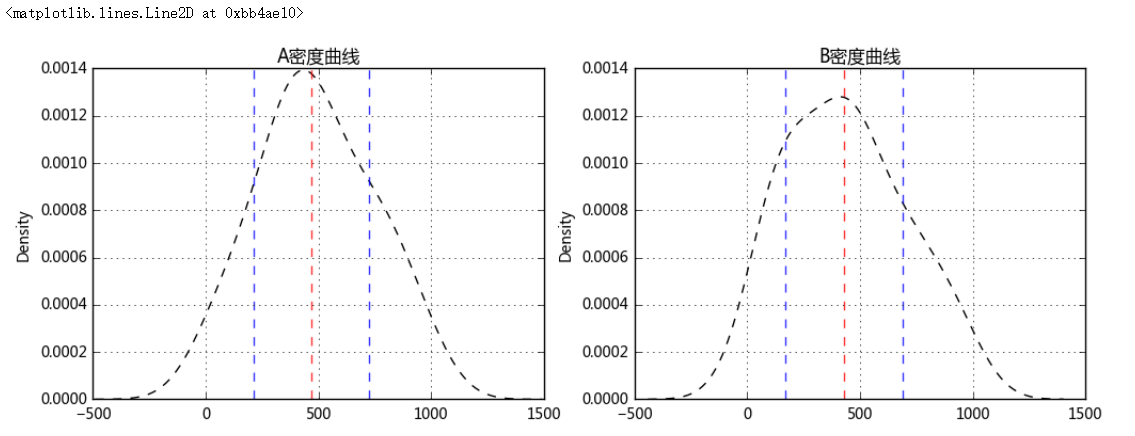
# 2、离中趋势度量 # (2)方差与标准差 a_std = sta.loc['std'] b_std = stb.loc['std'] a_var = data['A_sale'].var() b_var = data['B_sale'].var() print('A销售额的标准差为:%.2f, B销售额的标准差为:%.2f' % (a_std,b_std)) print('A销售额的方差为:%.2f, B销售额的方差为:%.2f' % (a_var,b_var)) # 方差 → 各组中数值与算数平均数离差平方的算术平均数 # 标准差 → 方差的平方根 # 标准差是最常用的离中趋势指标 → 标准差越大,离中趋势越明显 fig = plt.figure(figsize = (12,4)) ax1 = fig.add_subplot(1,2,1) data['A_sale'].plot(kind = 'kde',style = 'k--',grid = True,title = 'A密度曲线') plt.axvline(sta.loc['50%'],hold=None,color='r',linestyle="--",alpha=0.8) plt.axvline(sta.loc['50%'] - a_std,hold=None,color='b',linestyle="--",alpha=0.8) plt.axvline(sta.loc['50%'] + a_std,hold=None,color='b',linestyle="--",alpha=0.8) # A密度曲线,1个标准差 ax2 = fig.add_subplot(1,2,2) data['B_sale'].plot(kind = 'kde',style = 'k--',grid = True,title = 'B密度曲线') plt.axvline(stb.loc['50%'],hold=None,color='r',linestyle="--",alpha=0.8) plt.axvline(stb.loc['50%'] - b_std,hold=None,color='b',linestyle="--",alpha=0.8) plt.axvline(stb.loc['50%'] + b_std,hold=None,color='b',linestyle="--",alpha=0.8) # B密度曲线,1个标准差
输出:
A销售额的标准差为:255.51, B销售额的标准差为:260.38 A销售额的方差为:65287.16, B销售额的方差为:67796.90