对比分析
''' 【课程1.3】 对比分析 对比分析 → 两个互相联系的指标进行比较 绝对数比较(相减) / 相对数比较(相除) 结构分析、比例分析、空间比较分析、动态对比分析 '''
import numpy as np import pandas as pd import matplotlib.pyplot as plt % matplotlib inline
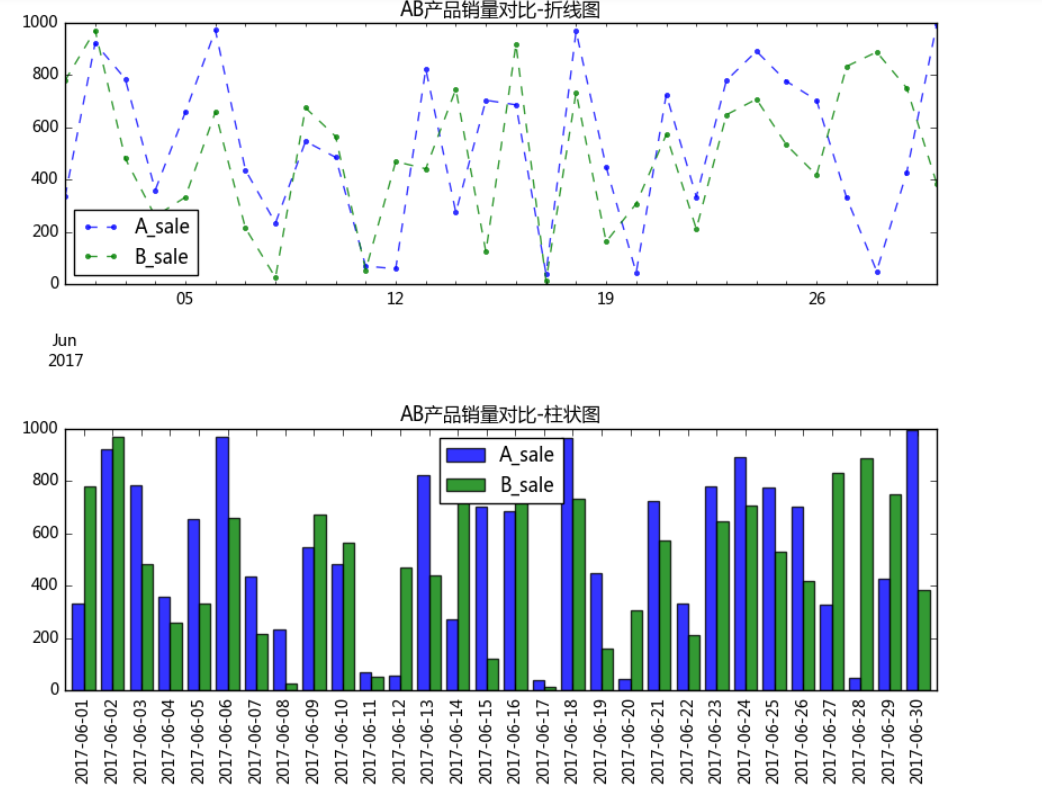
# 1、绝对数比较 → 相减 # 相互对比的指标在量级上不能差别过大 # (1)折线图比较 # (2)多系列柱状图比较 data = pd.DataFrame(np.random.rand(30,2)*1000, columns = ['A_sale','B_sale'], index = pd.period_range('20170601','20170630')) print(data.head()) # 创建数据 → 30天内A/B产品的日销售额 data.plot(kind='line', style = '--.', alpha = 0.8, figsize = (10,3), title = 'AB产品销量对比-折线图') # 折线图比较 data.plot(kind = 'bar', width = 0.8, alpha = 0.8, figsize = (10,3), title = 'AB产品销量对比-柱状图') # 多系列柱状图比较
输出:
A_sale B_sale 2017-06-01 334.812619 778.500279 2017-06-02 921.431743 970.734046 2017-06-03 785.444137 481.548456 2017-06-04 359.790330 259.824537 2017-06-05 657.224681 332.818389
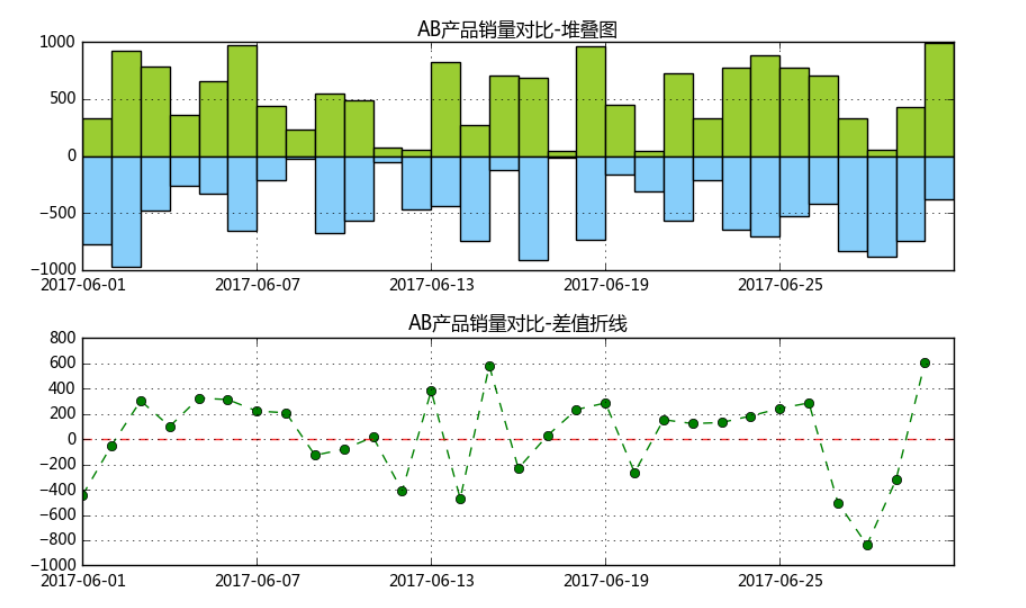
# 1、绝对数比较 → 相减 # (3)柱状图堆叠图+差值折线图比较 fig3 = plt.figure(figsize=(10,6)) plt.subplots_adjust(hspace=0.3) # 创建子图及间隔设置 ax1 = fig3.add_subplot(2,1,1) x = range(len(data)) y1 = data['A_sale'] y2 = -data['B_sale'] plt.bar(x,y1,width = 1,facecolor = 'yellowgreen') plt.bar(x,y2,width = 1,facecolor = 'lightskyblue') plt.title('AB产品销量对比-堆叠图') plt.grid() plt.xticks(range(0,30,6)) ax1.set_xticklabels(data.index[::6]) # 创建堆叠图 ax2 = fig3.add_subplot(2,1,2) y3 = data['A_sale']-data['B_sale'] plt.plot(x,y3,'--go') plt.axhline(0,hold=None,color='r',linestyle="--",alpha=0.8) # 添加y轴参考线 plt.grid() plt.title('AB产品销量对比-差值折线') plt.xticks(range(0,30,6)) ax2.set_xticklabels(data.index[::6]) # 创建差值折线图
输出:
[<matplotlib.text.Text at 0x9faa9b0>, <matplotlib.text.Text at 0x9fa6e48>, <matplotlib.text.Text at 0x9fed0f0>, <matplotlib.text.Text at 0x9fedb38>, <matplotlib.text.Text at 0x9ff15c0>]
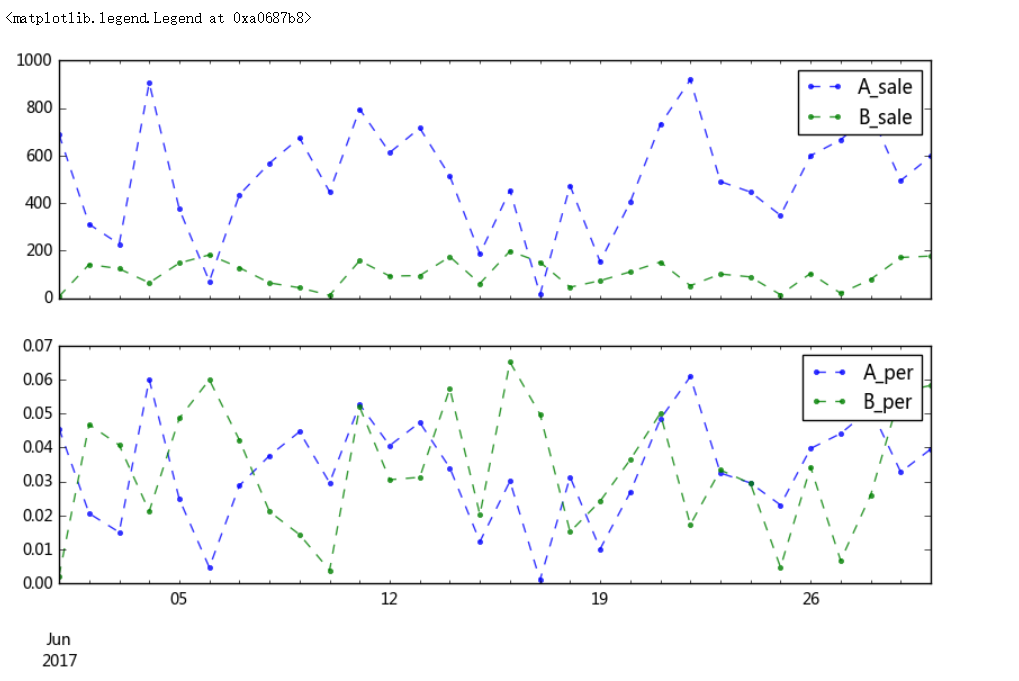
# 2、相对数比较 → 相除 # 有联系的指标综合计算后的对比,数值为相对数 # 结构分析、比例分析、空间比较分析、动态对比分析、计划完成度分析 # (1)结构分析 # 在分组基础上,各组总量指标与总体的总量指标对比,计算出各组数量在总量中所占比重 # 反映总体的内部结构 data = pd.DataFrame({'A_sale':np.random.rand(30)*1000, 'B_sale':np.random.rand(30)*200}, index = pd.period_range('20170601','20170630')) print(data.head()) print('------') # 创建数据 → 30天内A/B产品的日销售额 # A/B产品销售额量级不同 data['A_per'] = data['A_sale'] / data['A_sale'].sum() data['B_per'] = data['B_sale'] / data['B_sale'].sum() # 计算出每天的营收占比 data['A_per%'] = data['A_per'].apply(lambda x: '%.2f%%' % (x*100)) data['B_per%'] = data['B_per'].apply(lambda x: '%.2f%%' % (x*100)) # 转换为百分数 print(data.head()) fig,axes = plt.subplots(2,1,figsize = (10,6),sharex=True) data[['A_sale','B_sale']].plot(kind='line',style = '--.',alpha = 0.8,ax=axes[0]) axes[0].legend(loc = 'upper right') data[['A_per','B_per']].plot(kind='line',style = '--.',alpha = 0.8,ax=axes[1]) axes[1].legend(loc = 'upper right') # 绝对值对比较难看出结构性变化,通过看销售额占比来看售卖情况的对比 # 同时可以反应“强度” → 两个性质不同但有一定联系的总量指标对比,用来说明“强度”、“密度”、“普遍程度” # 例如:国内生产总值“元/人”,人口密度“人/平方公里”
输出:
A_sale B_sale 2017-06-01 688.134982 6.759655 2017-06-02 310.911156 141.978290 2017-06-03 227.496397 123.595400 2017-06-04 905.453084 64.534911 2017-06-05 374.572618 147.550005 ------ A_sale B_sale A_per B_per A_per% B_per% 2017-06-01 688.134982 6.759655 0.045606 0.002227 4.56% 0.22% 2017-06-02 310.911156 141.978290 0.020606 0.046780 2.06% 4.68% 2017-06-03 227.496397 123.595400 0.015077 0.040723 1.51% 4.07% 2017-06-04 905.453084 64.534911 0.060009 0.021263 6.00% 2.13% 2017-06-05 374.572618 147.550005 0.024825 0.048616 2.48% 4.86%
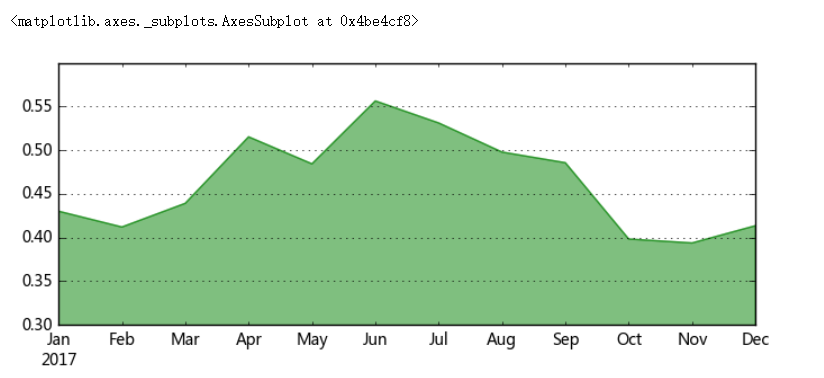
# 2、相对数比较 → 相除 # (2)比例分析 # 在分组的基础上,将总体不同部分的指标数值进行对比,其相对指标一般称为“比例相对数” # 比例相对数 = 总体中某一部分数值 / 总体中另一部分数值 → “基本建设投资额中工业、农业、教育投资的比例”、“男女比例”... data = pd.DataFrame({'consumption':np.random.rand(12)*1000 + 2000, 'salary':np.random.rand(12)*500 + 5000}, index = pd.period_range('2017/1','2017/12',freq = 'M')) print(data.head()) print('------') # 创建数据 → 某人一年内的消费、工资薪水情况 # 消费按照2000-3000/月随机,工资按照5000-5500/月随机 data['c_s'] = data['consumption'] / data['salary'] print(data.head()) # 比例相对数 → 消费收入比 data['c_s'].plot.area(color = 'green',alpha = 0.5,ylim = [0.3,0.6],figsize=(8,3),grid=True) # 创建面积图表达
输出:
consumption salary 2017-01 2300.613040 5349.939624 2017-02 2256.167470 5477.291974 2017-03 2356.130582 5366.495609 2017-04 2680.961342 5203.749452 2017-05 2612.676360 5395.189285 ------ consumption salary c_s 2017-01 2300.613040 5349.939624 0.430026 2017-02 2256.167470 5477.291974 0.411913 2017-03 2356.130582 5366.495609 0.439045 2017-04 2680.961342 5203.749452 0.515198 2017-05 2612.676360 5395.189285 0.484260
# 2、相对数比较 → 相除 # (3)空间比较分析(横向对比分析) # 同类现象在同一时间不同空间的指标数值进行对比,反应同类现象在不同空间上的差异程度和现象发展不平衡的状况 # 空间比较相对数 = 甲空间某一现象的数值 / 乙空间同类现象的数值 # 一个很现实的例子 → 绝对数来看,我国多经济总量世界第一,但从人均水平来看是另一回事 data = pd.DataFrame({'A':np.random.rand(30)*5000, 'B':np.random.rand(30)*2000, 'C':np.random.rand(30)*10000, 'D':np.random.rand(30)*800}, index = pd.period_range('20170601','20170630')) print(data.head()) print('------') # 创建数据 → 30天内A/B/C/D四个产品的销售情况 # 不同产品的销售量级不同 data.sum().plot(kind = 'bar',color = ['r','g','b','k'], alpha = 0.8, grid = True) for i,j in zip(range(4),data.sum()): plt.text(i-0.25,j+2000,'%.2f' % j, color = 'k') # 通过柱状图做横向比较 → 4个产品的销售额总量 data[:10].plot(kind = 'bar',color = ['r','g','b','k'], alpha = 0.8, grid = True, figsize = (12,4),width = 0.8) # 多系列柱状图,横向比较前十天4个产品的销售额 # 关于同比与环比 # 同比 → 产品A在2015.3和2016.3的比较(相邻时间段的同一时间点) # 环比 → 产品A在2015.3和2015.4的比较(相邻时间段的比较) # 如何界定“相邻时间段”与“时间点”,决定了是同比还是环比
输出:
A B C D 2017-06-01 2850.211921 1647.138351 5276.354493 529.747107 2017-06-02 3222.680792 768.466753 6941.803099 284.760211 2017-06-03 727.193796 1732.612257 3311.883561 332.427362 2017-06-04 2582.599603 444.224737 1829.401025 744.340597 2017-06-05 1756.352061 1731.221585 7583.832278 768.792895

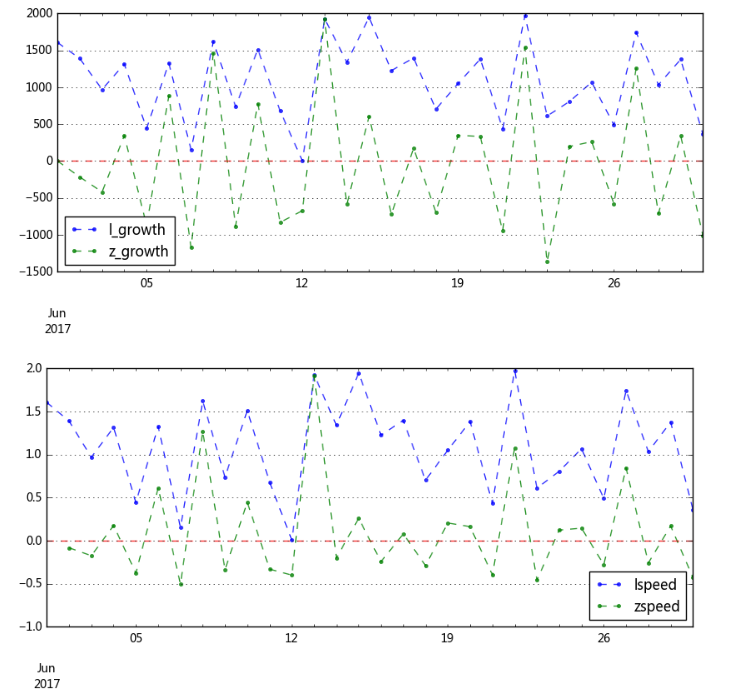
# 2、相对数比较 → 相除 # (4)动态对比分析(纵向对比分析) # 同一现象在不同时间上的指标数值进行对比,反应现象的数量随着时间推移而发展变动的程度及趋势 # 最基本方法,计算动态相对数 → 发展速度 # 动态相对数(发展速度) = 某一现象的报告期数值 / 同一现象的基期数值 # 基期:用来比较的基础时期 # 报告期:所要研究的时期,又称计算期 data = pd.DataFrame({'A':np.random.rand(30)*2000+1000}, index = pd.period_range('20170601','20170630')) print(data.head()) print('------') # 创建数据 → 30天内A产品的销售情况 data['base'] = 1000 # 假设基期销售额为1000,后面每一天都为计算期 data['l_growth'] = data['A'] - data['base'] # 累计增长量 = 报告期水平 - 固定基期水平 data['z_growth'] = data['A'] - data.shift(1)['A'] # 逐期增长量 = 报告期水平 - 报告期前一期水平 data[data.isnull()] = 0 # 替换缺失值 data[['l_growth','z_growth']].plot(figsize = (10,4),style = '--.',alpha = 0.8) plt.axhline(0,hold=None,color='r',linestyle="--",alpha=0.8) # 添加y轴参考线 plt.legend(loc = 'lower left') plt.grid() # 通过折线图查看增长量情况 data['lspeed'] = data['l_growth'] / data['base'] # 定基增长速度 data['zspeed'] = data['z_growth'] / data.shift(1)['A'] # 环比增长速度 data[['lspeed','zspeed']].plot(figsize = (10,4),style = '--.',alpha = 0.8) plt.axhline(0,hold=None,color='r',linestyle="--",alpha=0.8) # 添加y轴参考线 plt.grid() print(data.head()) print('------') # 通过折线图查看发展速度
输出:
A 2017-06-01 2604.901536 2017-06-02 2387.955402 2017-06-03 1968.693059 2017-06-04 2313.807035 2017-06-05 1441.483332 ------ A base l_growth z_growth lspeed zspeed 2017-06-01 2604.901536 1000 1604.901536 0.000000 1.604902 NaN 2017-06-02 2387.955402 1000 1387.955402 -216.946134 1.387955 -0.083284 2017-06-03 1968.693059 1000 968.693059 -419.262343 0.968693 -0.175574 2017-06-04 2313.807035 1000 1313.807035 345.113976 1.313807 0.175301 2017-06-05 1441.483332 1000 441.483332 -872.323703 0.441483 -0.377008 ------