Numpy基本数据结构
Numpy数组是一个多维数组对象,称为ndarray。其由两部分组成:
1 实际的数据
2 描述这些数据的元数据
一 ndarray的方法
# 多维数组ndarray import numpy as np ar = np.array([1,2,3,4,5,6,7]) print(ar) # 输出数组,注意数组的格式:中括号,元素之间没有逗号(和列表区分) print(ar.ndim) # 输出数组维度的个数(轴数),或者说“秩”,维度的数量也称rank print(ar.shape) # 数组的维度,对于n行m列的数组,shape为(n,m) print(ar.size) # 数组的元素总数,对于n行m列的数组,元素总数为n*m print(ar.dtype) # 数组中元素的类型,类似type()(注意了,type()是函数,.dtype是方法) print(ar.itemsize) # 数组中每个元素的字节大小,int32l类型字节为4,float64的字节为8 print(ar.data) # 包含实际数组元素的缓冲区,由于一般通过数组的索引获取元素,所以通常不需要使用这个属性。 ar # 交互方式下输出,会有array(数组) # 数组的基本属性 # ① 数组的维数称为秩(rank),一维数组的秩为1,二维数组的秩为2,以此类推 # ② 在NumPy中,每一个线性的数组称为是一个轴(axes),秩其实是描述轴的数量: # 比如说,二维数组相当于是两个一维数组,其中第一个一维数组中每个元素又是一个一维数组 # 所以一维数组就是NumPy中的轴(axes),第一个轴相当于是底层数组,第二个轴是底层数组里的数组。 # 而轴的数量——秩,就是数组的维数。
输出:
[1 2 3 4 5 6 7] 1 (7,) 7 int32 4 <memory at 0x0000027A3391FE88> array([1, 2, 3, 4, 5, 6, 7])
二 创建数组
1 利用array()函数
# 创建数组:array()函数,括号内可以是列表、元祖、数组、生成器等 ar1 = np.array(range(10)) # 整型 ar2 = np.array([1,2,3.14,4,5]) # 浮点型 ar3 = np.array([[1,2,3],('a','b','c')]) # 二维数组:嵌套序列(列表,元祖均可) ar4 = np.array([[1,2,3],('a','b','c','d')]) # 注意嵌套序列数量不一会怎么样 print(ar1,type(ar1),ar1.dtype) print(ar2,type(ar2),ar2.dtype) print(ar3,ar3.shape,ar3.ndim,ar3.size) # 二维数组,共6个元素 print(ar4,ar4.shape,ar4.ndim,ar4.size) # 一维数组,共2个元素
输出:
[0 1 2 3 4 5 6 7 8 9] <class 'numpy.ndarray'> int32 [ 1. 2. 3.14 4. 5. ] <class 'numpy.ndarray'> float64 [['1' '2' '3'] ['a' 'b' 'c']] (2, 3) 2 6 [[1, 2, 3] ('a', 'b', 'c', 'd')] (2,) 1 2
2 利用arrange()函数
# 创建数组:arange(),类似range(),在给定间隔内返回均匀间隔的值。 print(np.arange(10)) # 返回0-9,整型 print(np.arange(10.0)) # 返回0.0-9.0,浮点型 print(np.arange(5,12)) # 返回5-11 print(np.arange(5.0,12,2)) # 返回5.0-12.0,步长为2 print(np.arange(10000)) # 如果数组太大而无法打印,NumPy会自动跳过数组的中心部分,并只打印边角:
输出:
[0 1 2 3 4 5 6 7 8 9] [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] [ 5 6 7 8 9 10 11] [ 5. 7. 9. 11.] [ 0 1 2 ..., 9997 9998 9999]
3 利用linspace()函数
# 创建数组:linspace():返回在间隔[开始,停止]上计算的num个均匀间隔的样本。 ar1 = np.linspace(2.0, 3.0, num=5) ar2 = np.linspace(2.0, 3.0, num=5, endpoint=False) ar3 = np.linspace(2.0, 3.0, num=5, retstep=True) print(ar1,type(ar1)) print(ar2) print(ar3,type(ar3)) # numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None) # start:起始值,stop:结束值 # num:生成样本数,默认为50 # endpoint:如果为真,则停止是最后一个样本。否则,不包括在内。默认值为True。 # retstep:如果为真,返回(样本,步骤),其中步长是样本之间的间距 → 输出为一个包含2个元素的元祖,第一个元素为array,第二个为步长实际值
输出:
[ 2. 2.25 2.5 2.75 3. ] <class 'numpy.ndarray'> [ 2. 2.2 2.4 2.6 2.8] (array([ 2. , 2.25, 2.5 , 2.75, 3. ]), 0.25) <class 'tuple'>
4 利用zeros()/zeros_like()/ones()/ones_like()
# 创建数组:zeros()/zeros_like()/ones()/ones_like() ar1 = np.zeros(5) ar2 = np.zeros((2,2), dtype = np.int) print(ar1,ar1.dtype) print(ar2,ar2.dtype) print('------') # numpy.zeros(shape, dtype=float, order='C'):返回给定形状和类型的新数组,用零填充。 # shape:数组纬度,二维以上需要用(),且输入参数为整数 # dtype:数据类型,默认numpy.float64 # order:是否在存储器中以C或Fortran连续(按行或列方式)存储多维数据。 ar3 = np.array([list(range(5)),list(range(5,10))]) ar4 = np.zeros_like(ar3) print(ar3) print(ar4) print('------') # 返回具有与给定数组相同的形状和类型的零数组,这里ar4根据ar3的形状和dtype创建一个全0的数组 ar5 = np.ones(9) ar6 = np.ones((2,3,4)) ar7 = np.ones_like(ar3) print(ar5) print(ar6) print(ar7) # ones()/ones_like()和zeros()/zeros_like()一样,只是填充为1
输出:
[ 0. 0. 0. 0. 0.] float64 [[0 0] [0 0]] int32 ------ [[0 1 2 3 4] [5 6 7 8 9]] [[0 0 0 0 0] [0 0 0 0 0]] ------ [ 1. 1. 1. 1. 1. 1. 1. 1. 1.] [[[ 1. 1. 1. 1.] [ 1. 1. 1. 1.] [ 1. 1. 1. 1.]] [[ 1. 1. 1. 1.] [ 1. 1. 1. 1.] [ 1. 1. 1. 1.]]] [[1 1 1 1 1] [1 1 1 1 1]]
5 eye()
# 创建数组:eye() print(np.eye(5)) # 创建一个正方的N*N的单位矩阵,对角线值为1,其余为0
输出:
[[ 1. 0. 0. 0. 0.] [ 0. 1. 0. 0. 0.] [ 0. 0. 1. 0. 0.] [ 0. 0. 0. 1. 0.] [ 0. 0. 0. 0. 1.]]
三 ndarray的数据类型
bool 用一个字节存储的布尔类型(True或False) int 由所在平台决定其大小的整数(一般为int32或int64) int8 一个字节大小,-128 至 127 int16 整数,-32768 至 32767 int32 整数,-2 31 至 2 32 -1 int64 整数,-2 63 至 2 63 - 1 uint8 无符号整数,0 至 255 uint16 无符号整数,0 至 65535 uint32 无符号整数,0 至 2 ** 32 - 1 uint64 无符号整数,0 至 2 ** 64 - 1 float16 半精度浮点数:16位,正负号1位,指数5位,精度10位 float32 单精度浮点数:32位,正负号1位,指数8位,精度23位 float64或float 双精度浮点数:64位,正负号1位,指数11位,精度52位 complex64 复数,分别用两个32位浮点数表示实部和虚部 complex128或complex 复数,分别用两个64位浮点数表示实部和虚部
四 数组形状
数组形状:.T/.reshape()/.resize() ar1 = np.arange(10) ar2 = np.ones((5,2)) print(ar1,'\n',ar1.T) print(ar2,'\n',ar2.T) print('------') # .T方法:转置,例如原shape为(3,4)/(2,3,4),转置结果为(4,3)/(4,3,2) → 所以一维数组转置后结果不变 ar3 = ar1.reshape(2,5) # 用法1:直接将已有数组改变形状 ar4 = np.zeros((4,6)).reshape(3,8) # 用法2:生成数组后直接改变形状 ar5 = np.reshape(np.arange(12),(3,4)) # 用法3:参数内添加数组,目标形状 print(ar1,'\n',ar3) print(ar4) print(ar5) print('------') # numpy.reshape(a, newshape, order='C'):为数组提供新形状,而不更改其数据,所以元素数量需要一致!! ar6 = np.resize(np.arange(5),(3,4)) print(ar6) # numpy.resize(a, new_shape):返回具有指定形状的新数组,如有必要可重复填充所需数量的元素。 # 注意了:.T/.reshape()/.resize()都是生成新的数组!!!
输出:
[0 1 2 3 4 5 6 7 8 9] [0 1 2 3 4 5 6 7 8 9] [[ 1. 1.] [ 1. 1.] [ 1. 1.] [ 1. 1.] [ 1. 1.]] [[ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.]] ------ [0 1 2 3 4 5 6 7 8 9] [[0 1 2 3 4] [5 6 7 8 9]] [[ 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0.]] [[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11]] ------ [[0 1 2 3] [4 0 1 2] [3 4 0 1]]
五 数组的复制
# 数组的复制 ar1 = np.arange(10) ar2 = ar1 print(ar2 is ar1) ar1[2] = 9 print(ar1,ar2) # 回忆python的赋值逻辑:指向内存中生成的一个值 → 这里ar1和ar2指向同一个值,所以ar1改变,ar2一起改变 ar3 = ar1.copy() print(ar3 is ar1) ar1[0] = 9 print(ar1,ar3) # copy方法生成数组及其数据的完整拷贝 # 再次提醒:.T/.reshape()/.resize()都是生成新的数组!!!
输出:
True [0 1 9 3 4 5 6 7 8 9] [0 1 9 3 4 5 6 7 8 9] False [9 1 9 3 4 5 6 7 8 9] [0 1 9 3 4 5 6 7 8 9]
六 数组的类型转换
# 数组类型转换:.astype() ar1 = np.arange(10,dtype=float) print(ar1,ar1.dtype) print('-----') # 可以在参数位置设置数组类型 ar2 = ar1.astype(np.int32) print(ar2,ar2.dtype) print(ar1,ar1.dtype) # a.astype():转换数组类型 # 注意:养成好习惯,数组类型用np.int32,而不是直接int32
输出:
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] float64 ----- [0 1 2 3 4 5 6 7 8 9] int32 [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] float64
七 数组堆叠
a = np.arange(5) # a为一维数组,5个元素 b = np.arange(5,9) # b为一维数组,4个元素 ar1 = np.hstack((a,b)) # 注意:((a,b)),这里形状可以不一样 print(a,a.shape) print(b,b.shape) print(ar1,ar1.shape) a = np.array([[1],[2],[3]]) # a为二维数组,3行1列 b = np.array([['a'],['b'],['c']]) # b为二维数组,3行1列 ar2 = np.hstack((a,b)) # 注意:((a,b)),这里形状必须一样 print(a,a.shape) print(b,b.shape) print(ar2,ar2.shape) print('-----') # numpy.hstack(tup):水平(按列顺序)堆叠数组 a = np.arange(5) b = np.arange(5,10) ar1 = np.vstack((a,b)) print(a,a.shape) print(b,b.shape) print(ar1,ar1.shape) a = np.array([[1],[2],[3]]) b = np.array([['a'],['b'],['c'],['d']]) ar2 = np.vstack((a,b)) # 这里形状可以不一样 print(a,a.shape) print(b,b.shape) print(ar2,ar2.shape) print('-----') # numpy.vstack(tup):垂直(按列顺序)堆叠数组 a = np.arange(5) b = np.arange(5,10) ar1 = np.stack((a,b)) ar2 = np.stack((a,b),axis = 1) print(a,a.shape) print(b,b.shape) print(ar1,ar1.shape) print(ar2,ar2.shape) # numpy.stack(arrays, axis=0):沿着新轴连接数组的序列,形状必须一样! # 重点解释axis参数的意思,假设两个数组[1 2 3]和[4 5 6],shape均为(3,0) # axis=0:[[1 2 3] [4 5 6]],shape为(2,3) # axis=1:[[1 4] [2 5] [3 6]],shape为(3,2)
输出:
[0 1 2 3 4] (5,) [5 6 7 8] (4,) [0 1 2 3 4 5 6 7 8] (9,) [[1] [2] [3]] (3, 1) [['a'] ['b'] ['c']] (3, 1) [['1' 'a'] ['2' 'b'] ['3' 'c']] (3, 2) ----- [0 1 2 3 4] (5,) [5 6 7 8 9] (5,) [[0 1 2 3 4] [5 6 7 8 9]] (2, 5) [[1] [2] [3]] (3, 1) [['a'] ['b'] ['c'] ['d']] (4, 1) [['1'] ['2'] ['3'] ['a'] ['b'] ['c'] ['d']] (7, 1) ----- [0 1 2 3 4] (5,) [5 6 7 8 9] (5,) [[0 1 2 3 4] [5 6 7 8 9]] (2, 5) [[0 5] [1 6] [2 7] [3 8] [4 9]] (5, 2)
八 数组拆分
# 数组拆分 ar = np.arange(16).reshape(4,4) ar1 = np.hsplit(ar,2) print(ar) print(ar1,type(ar1)) # numpy.hsplit(ary, indices_or_sections):将数组水平(逐列)拆分为多个子数组 → 按列拆分 # 输出结果为列表,列表中元素为数组 ar2 = np.vsplit(ar,4) print(ar2,type(ar2)) # numpy.vsplit(ary, indices_or_sections)::将数组垂直(行方向)拆分为多个子数组 → 按行拆
输出:
[[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11] [12 13 14 15]] [array([[ 0, 1], [ 4, 5], [ 8, 9], [12, 13]]), array([[ 2, 3], [ 6, 7], [10, 11], [14, 15]])] <class 'list'> [array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8, 9, 10, 11]]), array([[12, 13, 14, 15]])] <class 'list'>
九 数组的简单运算
# 数组简单运算 ar = np.arange(6).reshape(2,3) print(ar + 10) # 加法 print(ar * 2) # 乘法 print(1 / (ar+1)) # 除法 print(ar ** 0.5) # 幂 # 与标量的运算 print(ar.mean()) # 求平均值 print(ar.max()) # 求最大值 print(ar.min()) # 求最小值 print(ar.std()) # 求标准差 print(ar.var()) # 求方差 print(ar.sum(), np.sum(ar,axis = 0)) # 求和,np.sum() → axis为0,按列求和;axis为1,按行求和 print(np.sort(np.array([1,4,3,2,5,6]))) # 排序 # 常用函数
输出:
[[10 11 12] [13 14 15]] [[ 0 2 4] [ 6 8 10]] [[ 1. 0.5 0.33333333] [ 0.25 0.2 0.16666667]] [[ 0. 1. 1.41421356] [ 1.73205081 2. 2.23606798]] 2.5 5 0 1.70782512766 2.91666666667 15 [3 5 7] [1 2 3 4 5 6]
十 Numpy索引及切片
1 基本索引
# 基本索引及切片 ar = np.arange(20) print(ar) print(ar[4]) print(ar[3:6]) print('-----') # 一维数组索引及切片 ar = np.arange(16).reshape(4,4) print(ar, '数组轴数为%i' %ar.ndim) # 4*4的数组 print(ar[2], '数组轴数为%i' %ar[2].ndim) # 切片为下一维度的一个元素,所以是一维数组 print(ar[2][1]) # 二次索引,得到一维数组中的一个值 print(ar[1:3], '数组轴数为%i' %ar[1:3].ndim) # 切片为两个一维数组组成的二维数组 print(ar[2,2]) # 切片数组中的第三行第三列 → 10 print(ar[:2,1:]) # 切片数组中的1,2行、2,3,4列 → 二维数组 print('-----') # 二维数组索引及切片 ar = np.arange(8).reshape(2,2,2) print(ar, '数组轴数为%i' %ar.ndim) # 2*2*2的数组 print(ar[0], '数组轴数为%i' %ar[0].ndim) # 三维数组的下一个维度的第一个元素 → 一个二维数组 print(ar[0][0], '数组轴数为%i' %ar[0][0].ndim) # 三维数组的下一个维度的第一个元素下的第一个元素 → 一个一维数组 print(ar[0][0][1], '数组轴数为%i' %ar[0][0][1].ndim) # **三维数组索引及切片
输出:
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19] 4 [3 4 5] ----- [[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11] [12 13 14 15]] 数组轴数为2 [ 8 9 10 11] 数组轴数为1 9 [[ 4 5 6 7] [ 8 9 10 11]] 数组轴数为2 10 [[1 2 3] [5 6 7]] ----- [[[0 1] [2 3]] [[4 5] [6 7]]] 数组轴数为3 [[0 1] [2 3]] 数组轴数为2 [0 1] 数组轴数为1 1 数组轴数为0
2 布尔型索引
# 布尔型索引及切片 ar = np.arange(12).reshape(3,4) i = np.array([True,False,True]) j = np.array([True,True,False,False]) print(ar) print(i) print(j) print(ar[i,:]) # 在第一维度做判断,只保留True,这里第一维度就是行,ar[i,:] = ar[i](简单书写格式) print(ar[:,j]) # 在第二维度做判断,这里如果ar[:,i]会有警告,因为i是3个元素,而ar在列上有4个 # 布尔型索引:以布尔型的矩阵去做筛选 m = ar > 5 print(m) # 这里m是一个判断矩阵 print(ar[m]) # 用m判断矩阵去筛选ar数组中>5的元素 → 重点!后面的pandas判断方式原理就来自此处
输出:
[[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11]] [ True False True] [ True True False False] [[ 0 1 2 3] [ 8 9 10 11]] [[0 1] [4 5] [8 9]] [[False False False False] [False False True True] [ True True True True]] [ 6 7 8 9 10 11]
3
# 数组索引及切片的值更改、复制 ar = np.arange(10) print(ar) ar[5] = 100 ar[7:9] = 200 print(ar) # 一个标量赋值给一个索引/切片时,会自动改变/传播原始数组 ar = np.arange(10) b = ar.copy() b[7:9] = 200 print(ar) print(b) # 复制
输出:
[0 1 2 3 4 5 6 7 8 9] [ 0 1 2 3 4 100 6 200 200 9] [0 1 2 3 4 5 6 7 8 9] [ 0 1 2 3 4 5 6 200 200 9]
十一 Numpy随机数
numpy.random包含多种概率分布的随机样本,是数据分析辅助的重点工具之一 # 随机数生成 samples = np.random.normal(size=(4,4)) print(samples) # 生成一个标准正太分布的4*4样本值
输出:
[[ 0.17875618 -1.19367146 -1.29127688 1.11541622] [ 1.48126355 -0.81119863 -0.94187702 -0.13203948] [ 0.11418808 -2.34415548 0.17391121 1.4822019 ] [ 0.46157021 0.43227682 0.58489093 0.74553395]]
# numpy.random.rand(d0, d1, ..., dn):生成一个[0,1)之间的随机浮点数或N维浮点数组 —— 均匀分布 import matplotlib.pyplot as plt # 导入matplotlib模块,用于图表辅助分析 % matplotlib inline # 魔法函数,每次运行自动生成图表 a = np.random.rand() print(a,type(a)) # 生成一个随机浮点数 b = np.random.rand(4) print(b,type(b)) # 生成形状为4的一维数组 c = np.random.rand(2,3) print(c,type(c)) # 生成形状为2*3的二维数组,注意这里不是((2,3)) samples1 = np.random.rand(1000) samples2 = np.random.rand(1000) plt.scatter(samples1,samples2) # 生成1000个均匀分布的样本值
输出:
0.3671245126484347 <class 'float'> [ 0.95365841 0.45627035 0.71528562 0.98488116] <class 'numpy.ndarray'> [[ 0.82284657 0.95853197 0.87376954] [ 0.53341526 0.17313861 0.18831533]] <class 'numpy.ndarray'> <matplotlib.collections.PathCollection at 0x7bb52e8>

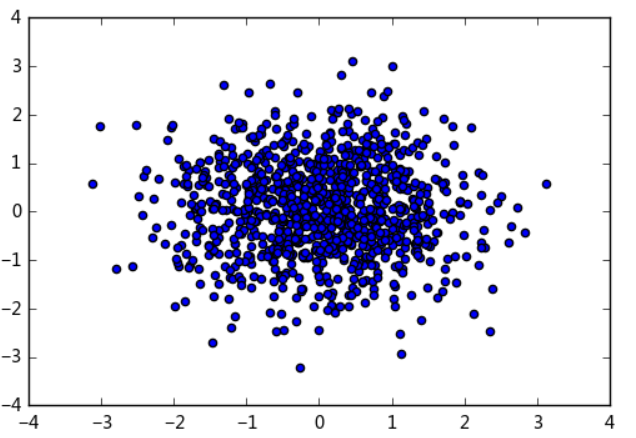
# numpy.random.randn(d0, d1, ..., dn):生成一个浮点数或N维浮点数组 —— 正态分布 samples1 = np.random.randn(1000) samples2 = np.random.randn(1000) plt.scatter(samples1,samples2) # randn和rand的参数用法一样 # 生成1000个正太的样本值
输出:
<matplotlib.collections.PathCollection at 0x842ea90>
# numpy.random.randint(low, high=None, size=None, dtype='l'):生成一个整数或N维整数数组 # 若high不为None时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数,且high必须大于low # dtype参数:只能是int类型 print(np.random.randint(2)) # low=2:生成1个[0,2)之间随机整数 print(np.random.randint(2,size=5)) # low=2,size=5 :生成5个[0,2)之间随机整数 print(np.random.randint(2,6,size=5)) # low=2,high=6,size=5:生成5个[2,6)之间随机整数 print(np.random.randint(2,size=(2,3))) # low=2,size=(2,3):生成一个2x3整数数组,取数范围:[0,2)随机整数 print(np.random.randint(2,6,(2,3))) # low=2,high=6,size=(2,3):生成一个2*3整数数组,取值范围:[2,6)随机整数
输出:
0 [0 1 1 0 1] [2 5 2 3 5] [[0 1 1] [1 1 1]] [[4 4 3] [2 3 3]]
十二 numpy读取/写入
# 存储数组数据 .npy文件 import os os.chdir('C:/Users/Hjx/Desktop/') ar = np.random.rand(5,5) print(ar) np.save('arraydata.npy', ar) # 也可以直接 np.save('C:/Users/Hjx/Desktop/arraydata.npy', ar)
输出:
[[ 0.57358458 0.71126411 0.22317828 0.69640773 0.97406015] [ 0.83007851 0.63460575 0.37424462 0.49711017 0.42822812] [ 0.51354459 0.96671598 0.21427951 0.91429226 0.00393325] [ 0.680534 0.31516091 0.79848663 0.35308657 0.21576843] [ 0.38634472 0.47153005 0.6457086 0.94983697 0.97670458]]
# 读取数组数据 .npy文件 ar_load =np.load('arraydata.npy') print(ar_load) # 也可以直接 np.load('C:/Users/Hjx/Desktop/arraydata.npy')
输出:
[[ 0.57358458 0.71126411 0.22317828 0.69640773 0.97406015] [ 0.83007851 0.63460575 0.37424462 0.49711017 0.42822812] [ 0.51354459 0.96671598 0.21427951 0.91429226 0.00393325] [ 0.680534 0.31516091 0.79848663 0.35308657 0.21576843] [ 0.38634472 0.47153005 0.6457086 0.94983697 0.97670458]]
# 存储/读取文本文件 ar = np.random.rand(5,5) np.savetxt('array.txt',ar, delimiter=',') # np.savetxt(fname, X, fmt='%.18e', delimiter=' ', newline='\n', header='', footer='', comments='# '):存储为文本txt文件 ar_loadtxt = np.loadtxt('array.txt', delimiter=',') print(ar_loadtxt) # 也可以直接 np.loadtxt('C:/Users/Hjx/Desktop/array.txt')
输出:
[[ 0.28280684 0.66188985 0.00372083 0.54051044 0.68553963] [ 0.9138449 0.37056825 0.62813711 0.83032184 0.70196173] [ 0.63438739 0.86552157 0.68294764 0.2959724 0.62337767] [ 0.67411154 0.87678919 0.53732168 0.90366896 0.70480366] [ 0.00936579 0.32914898 0.30001813 0.66198967 0.04336824]]

