统计学方法论
# 数据类型分为两种,一种是数值类型,数值还可以继续分为离散型,连续型。 # 一种是种类,还可以分为可以区分等级的种类(县长,市长,省长),和不可以区分等级的种类(苹果,橘子)。 # 数据的统计性分析,可以分为描述性统计和 推断统计 # 描述性统计 # 频数/频率 # 集中趋势 # 数值 用 平均值,中位数 # 种类 用众数 # 分位数 # 离散程度 # 用方差,平方差。(离散程度,不稳定性)(极值不推荐,表达的含义不够多) # 分布形状 # 峰度:kurt 峰度大于0,表示集中趋势更明显,比标准分布更集中。 # 偏度:skew # 峰度和偏度都是可以小于0的。 # 方法 # 峰度 kurt() # 偏度skew() # 分位数 describe(percentiles=[0.2,0.3,0.9]) # np.mod(arr,2) # np.modf(arr) # np.ceil() # np.floor()

# 推断统计
# 点估计
# 容易受随机抽样的影响
# 区间估计
# --> 置信区间,置信度 --> 由中心极限定理 和 正态曲线 推出。
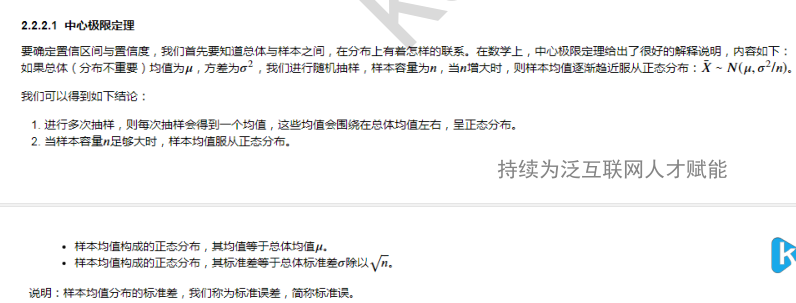
概念说明 标准差和标准误的区别 https://wiki.mbalib.com/wiki/%E6%A0%87%E5%87%86%E8%AF%AF%E5%B7%AE 标准差与标准误的意义、作用和使用范围均不同。标准差(亦称单数标准差)一般用s表示,是表示个体间变异大小的指标,反映了整个样本对样本平均数的离散程度,是数据精密度的衡量指标;
而标准误一般用s_{\bar{x}}表示,反映样本平均数对总体平均数的变异程度,从而反映抽样误差的大小,是量度结果精密度的指标。随着样本数(或测量次数)n的增大,标准差趋向某个稳定值,
即样本标准差s越接近总体标准差σ,而标准误则随着样本数(或测量次数)n的增大逐渐减小,即样本平均数越接近总体平均数μ;故在实验中也经常采用适当增加样本数(或测量次数)n减小s_{\bar{x}}
的方法来减小实验误差,但样本数太大意义也不大。标准差是最常用的统计量,一般用于表示一组样本变量的分散程度;标准误一般用于统计推断中,主要包括假设检验和参数估计,如样本平均数的假设检验、
参数的区间估计与点估计等。标准差与标准误既有明显区别,又密切相关:标准误是标准差的1/\sqrt{n};二者都是衡量样本变量(观测值)随机性的指标,只是从不同角度来反映误差;二者在统计推断和
误差分析中都有重要的应用 假设检验 https://wiki.mbalib.com/wiki/%E5%81%87%E8%AE%BE%E6%A3%80%E9%AA%8C 显著性水平 https://wiki.mbalib.com/wiki/%E6%98%BE%E8%91%97%E6%80%A7%E6%B0%B4%E5%B9%B3 指当原假设为正确时人们却把它拒绝了的概率或风险。显著性水平代表的意义是在一次试验中小概率事物发生的可能性大小。 显著性水平不是一个固定不变的数值,依据拒绝区间所可能承担的风险来决定 显著性差异 当数据之间具有了显著性差异,就说明参与比对的数据不是来自于同一总体。 显著性差异是一种有量度的或然性评价。比如,我们说A、B两数据在0.05水平上具备显著性差异,这是说两组数据具备显著性差异的可能性为95%。两个数据所代表的样本还有5%的可能性是没有差异的。
这5%的差异是由于随机误差造成的。 P-value是原假设H0真实的结论时,我们观察到样本的值有多大的概率,简称P值。如果此值小,就下原假设为不真实的结论。统计学上称为小概率事件,即样本不是从原假设的分布中抽出的。
一般P值大于α,则无法拒绝原假设,相反,P值小于α,则拒绝原假设。通常情况下,实验结果达到0.05水平或0.01水平,才可以说数据之间具备了显著性差异。 显著性假设 https://wiki.mbalib.com/wiki/%E6%98%BE%E8%91%97%E6%80%A7%E6%A3%80%E9%AA%8C Z检验 https://wiki.mbalib.com/wiki/Z%E6%A3%80%E9%AA%8C T检验 https://wiki.mbalib.com/wiki/T%E6%A3%80%E9%AA%8C
Z检验和T检验 都是判断样本均值是否与总体均值有显著性差异、
试题: iris数据,在总体标准差不知道的情况下,求花瓣宽度在95%置信度下的置信区间 1 样本均值 --> data.mean() 2 标准误 --> data.std() / len(data)**0.5 3 z分布95%置信度 大约是在2倍标准差,索引置信区间是 [均值-2*标准误,均值+2*标准误] 注意 反思,感受
线性回归
线性回归 由监督学习引出来。 监督学习的重要概念 每当想要根据给定输入预测某个结果,并且还有输入—输出对的示例时,都应该使用监督学习。 特征 --> 相当于 x 标签 --> 相当于 y 监督学习的两大分类 回归 & 分类 from sklearn.linear_model import LinearRegression from sklearn.model_selection import train_test_split from sklearn.metrics import mean_squared_error,mean_absolute_error,r2_score lr = LinearRegression() x_train,x_test,y_train,y_test = train_test_split(res[:,:1],res[:,1:],train_size=0.75,random_state=2) lr.fit(x_train,y_train) lr.coef_ lr.intercept_ y_prdict = lr.predict(x_test) lr.score(x_train,y_train) # R2 推荐用R2指标进行衡量。 在训练值R**2的取值范围是[0,1],在测试集,R**2的取值范围是 [负无穷,1] # mean_squared_error(MSE) 均方误差 # np.sqrt(mean_squared_error) RMSE 根均方误差 # mean_absolute_error MAE 平均绝对值误差
逻辑回归 logistic回归与多重线性回归实际上有很多相同之处,最大的区别就在于他们的因变量不同,其他的基本都差不多,正是因为如此,这两种回归可以归于同一个家族,即广义线性模型
(generalized linear model)。这一家族中的模型形式基本上都差不多,不同的就是因变量不同,如果是连续的,就是多重线性回归,如果是二项分布,就是logistic回归,
如果是poisson分布,就是poisson回归,如果是负二项分布,就是负二项回归,等等。只要注意区分它们的因变量就可以了。 logistic回归的因变量可以是二分类的,也可以是多分类的,
但是二分类的更为常用,也更加容易解释。所以实际中最为常用的就是二分类的logistic回归。 Sigmoid函数是一个在生物学中常见的S型函数,也称为S型生长曲线。[1]在信息科学中,由于其单增以及反函数单增等性质,Sigmoid函数常被用作神经网络的阈值函数,将变量映射到0,1之间。 绘制决策边界
from matplotlib.colors import ListedColormap
def decision_boundary(model,X,y):
color = ['r','g','b']
marker = ['o','x','d']
class_label = np.unique(y)
cmap = ListedColormap(color[:len(class_label)])
x1_min,x2_min = np.min(X,axis=0) # 每一列的最小值
x1_max,x2_max = np.max(X,axis=0) # 每一列的最大值
x1 = np.arange(x1_min-1,x1_max+1,0.02) # x1列 从小到大,分
x2 = np.arange(x2_min-1,x2_max+1,0.02) # x2列 从小到大 分
X1,X2 = np.meshgrid(x1,x2) # X1,X2 都是 len(x2)*len(x1) 的多维数组 用meshgrid在二维平面中将每一个x和每一个y分别对应起来,编织成栅格。
# 可以这么理解,meshgrid函数用两个坐标轴上的点在平面上画网格。
z = lr.predict(np.array([X1.ravel(),X2.ravel()]).T).reshape(X1.shape)
plt.contourf(X1,X2,z,cmap=cmap,alpha=0.5) # plt.contourf 应用场景:等高线
for i,class_ in enumerate(class_label):
plt.scatter(x=X[y==class_,0],y=X[y==class_,1],c=cmap.colors[i],label=class_,marker=marker[i])
plt.legend()
几个方法 .ravel() .reshape(1,-1)的区别 是 ravel 是一维,reshape是二维。 lr.fit() lr.score() lr.predict() lr.predict_proba()
plt.legend(bbox_to_anchor= )
回归系列之L1和L2正则化
https://www.jianshu.com/p/a47c46153326
# 分类模型评估 # 混淆矩阵 TP(真阳性) TN(真阴性) FP(假阳性) FN(假阴性) # 对分类模型的评估有以下几种指标: 正确率,精准率,召回率,F1(调和平均值)。 # 正确率 预测正确的结果占总样本的百分比 # 正确率 = TP + TN / TP + TN + FP + FN # 虽然准确率能够判断总的正确率,但是在样本不均衡的情况下,并不能作为很好的指标来衡量结果。 # 比如在样本集中,正样本有90个,负样本有10个,样本是严重的不均衡。对于这种情况,我们只需要将全部样本预测为正样本,就能得到90%的准确率,但是完全没有意义。对于新数据,完全体现不出准确率。
# 因此,在样本不平衡的情况下,得到的高准确率没有任何意义,此时准确率就会失效。所以,我们需要寻找新的指标来评价模型的优劣。 # 精准率 是针对预测结果而言的,其含义是在被所有预测为正的样本中实际为正样本的概率。又叫查准率 # 精准率 = TP / TP + FP # 精准率和正确率看上去有些类似,但是是两个完全不同的概念。精准率代表对正样本结果中的预测准确程度,正确率则代表整体的预测准确程度,包括正样本和负样本 # 召回率 针对原样本而言的,其含义是在实际为正的样本中被预测为正样本的概率。又叫查全率 # 召回率 = TP / TP + FN # F1分数 # 我们希望精确率和召回率都很高,但实际上是矛盾的,上述两个指标是矛盾体,无法做到双高。因此,选择合适的阈值点,就需要根据实际问题需求,比如我们想要很高的精确率,就要牺牲掉一些召回率。想
@ 要得到很高的召回率,就要牺牲掉一些精准率。但通常情况下,我们可以根据他们之间的平衡点,定义一个新的指标,这就是F1 # F1分数同时考虑精确率和召回率,让两者同时达到最高 F1 = 2 * 精准率 * 召回率 / 精准率 + 召回率 # 真正率和假正率 # 真正率TPR = 灵敏度(Sensitivity) = TP/(TP+FN) # 假正率FPR = 1-特异度(Specificity) = FP/(FP+TN) # TPR和FPR分别是基于实际表现1、0出发的,也就是说在实际的正样本和负样本中来观察相关概率问题。因此,无论样本是否均衡,都不会被影响 # ROC曲线 # 横坐标为假正率(FPR),纵坐标为真正率(TPR) # ROC曲线也是通过遍历所有阈值来绘制曲线的。如果我们不断的遍历所有阈值,预测的正样本和负样本是在不断变化的,相应的ROC曲线TPR和FPR也会沿着曲线滑动 # 同时,我们也会思考,如何判断ROC曲线的好坏呢?我们来看,FPR表示模型虚报的程度,TPR表示模型预测覆盖的程度。理所当然的,我们希望虚报的越少越好,覆盖的越多越好。所以TPR越高,同时FPR越低,
# 也就是ROC曲线越陡,那么模型的性能也就越好 # 最后,我们来看一下,不论样本比例如何改变,ROC曲线都没有影响,也就是ROC曲线无视样本间的不平衡问题 # AUC # 表示ROC中曲线下的面积,用于判断模型的优劣 # 连接对角线的面积刚好是0.5,对角线的含义也就是随机判断预测结果,正负样本覆盖应该都是50%。另外,ROC曲线越陡越好,所以理想值是1,即正方形。所以AUC的值一般是介于0.5和1之间的 # 0.5-0.7:效果较低。 # 0.7-0.85:效果一般。 # 0.85-0.95:效果很好。 # 0.95-1:效果非常好 from sklearn.metrics import confusion_matrix,accuracy_score,precision_score,recall_score,f1_score,classification_report,auc,roc_curve,roc_auc_score fpr,tpr,thresholds = roc_curve(y_true=,y_score,pos_label=1,) # auc(fpr,tpr) = roc_auc_score(y_true=,y_score=)
#方法
# plt.matshow()
# 绘制ROC曲线 计算AUC面积
pro = lr.predict_proba(x_test)
fpr,tpr,thresholds = roc_curve(y_test,pro[:,1],pos_label=1)
plt.plot(fpr,tpr)
print(auc(fpr,tpr))
ROC曲线的意义 ROC曲线其实是诊断试验中用于展示某个判断原则效果好差的一种图形,可以通过AUC来衡量大小 实际工作中,一般AUC在0.7-0.9范围内的比较常见。超过0.9的属于凤毛麟角了
AQI 项目实战
# 完整的数据分析会用到的方面 # 描述性统计分析 # 推断统计分析 # 相关系数分析 # 区间估计http://localhost:8888/notebooks/Untitled.ipynb# # 统计建模 #步骤如下 # 明确目标 # 应用场景 # 哪些城市的空气质量较好/较差? -- 描述性 # 空气质量在地理分布上,是否具有一定的规律性? -- 描述性 # 沿海城市的空气质量是否有别于内陆城市? -- 推断性,独立两样本T检验 stats.levene / stats.ttest_ind # 空气质量主要受那些因素影响? -- 相关系数分析 sns.pairplot()-->视觉效果,直观 / corr(),heatmap() --> 更准确的衡量 # 全国城市空气质量普遍处于何种水平? -- 推断统计 区间估计 T统计 stats.t.interval # 怎样预测一个城市的空气质量? -- 统计建模 这实际已经是机器学习的范畴了。线性回归,RFECV,数据分箱,残差图,线性回归 # 获取数据 # 爬取数据 # 买数据 # ... # 数据整合 # 应用场景: 可能有两个csv,可能从数据库读两张表 # 横向整合 left on ,merge # 纵向整合 union concat # 数据清洗 # 初看数据 # head() # 缺失值 # 方法 # info() # isnull() # 数值类型用中位数,均值填充。 # 偏度大,选择中位数。 可以用直方图,或者 skew()方法。>0 ,表示正偏度/右偏态,右边的尾巴更长,分布的主题集中在左侧。 # 类别类型用众数,如果缺失的特别多,新增一列,单独作为一个类别,参与后续建模。 # 异常值 # describe()简单判断 # 进一步判断 # 箱型图 # 3σ准则 # 相关异常检测算法 # 处理方式 # 删除 # 视为缺失值处理 # 取对数 # np.log() 这是以 e 为底。其它形式是np.log2,np.log10 。现实世界的GDP 就是右偏态分布,取对数后,可能变为正态分布。 # 为了建模准确 # 局限 # 适用于右偏态,不适用左偏态 # 要求值都为正 # 取箱型图或3σ的临界值填充 # 使用分箱法 离散化处理 # 重复值 # 判断 duplicated() # 去重 drop_duplicates() # 可以在清洗完后,合适的情况下,在数据加上一列,辅助下一步的分析。 # apply()方法。 # 传入自定义函数 # 数据分析 # 描述统计
# sns.barplot(x='City',y='AQI',data=data[['City','AQI']].sort_values(by='AQI').iloc[:5])
# barplot是分类plot(Categorical plots)
# City是分类类型,AQI是数值类型。根据排序,选择最大的某类,前几的某类。应用此方法 -- 同时选择,sort_values(by=数值类型)
# 均值 # 中位数 # 最大值 # 众数 # 推断统计 # 应用场景: 根据样本,给出整体均值的置信区间 # 点估计 # 区间估计 # T统计 # from scipy import stats # stats.ttest_1samp() --> 返回的是T值和P值 # 在样本比较大的情况下,样本数量大于30,可以用 样本均值 +- 2倍的标准误。此时T分布已经和正态分布差不多了 # sstats.t.interval(置信度,样本自由度,样本均值,样本标准误) 样本自由度 = 样本数目 - 1 # Z统计 比较少,因为整体的方差未知 # 数据建模 # 应用场景:预测不同城市,(自变量有纬度,温度,GDP,是否临海)的空气质量系数。 这实际上已经涉及到机器学习了。 # 准备工作 #不同列之间的相关性分析 # sns.pairplot --> 图形显示直观,但没有数值化,无法准确衡量(一般很难看出线性关系) # df.corr() --> 可以用 sns.heatmap 进行可视化 # 对变量进行处理,纬度,温度,GDP是数值类型,不用处理,是否临海是类别变量,需要进行离散化处理。 # 类别变量如果只有两个,映射成 0,1 就 ok。 # 可以使用 series.map() map比python内置的map方法还要强大,这里可以传入函数或者字典。当前场景,字典更为方便。 # 类别变量如果大于两个 --> one hot # 处理过程 # 基模型 # 类别变量离散化处理后,做的第一个不完善的模型,直接线性回归,当然大概率不会太准。 # 特征选择 # from sklearn.feature_selection import RFECV # rfecv = RFECV(estimator=lr,step=1,cv=5,scoring='r2',n_jobs=-1) # estimator 要操作的模型 # step 每次删除的变量,默认为1 # cv 使用的交叉验证折数 # n_jobs 并发的数量 # scoring 评估的方式 # rfecv.fit(x_test,y_test) # print(rfecv.n_features_) # 返回经过选择之后,剩余的特征数量 # print(rfecv.estimator_) # 返回经过特征筛选后,使用缩减特征训练后的模型 # print(rfecv.support_) # 返回布尔值数组,用来表示特征是否被筛选 # print(rfecv.ranking_) # 返回每个特征的等级,数值越小,特征越重要 # print(rfecv.grid_scores_) # 返回对应数量特征时,模型的评分 # 处理成筛选后的特征 & 缩减后的特征构建的模型得分 # x_test_eli = rfecv.transform(x_test) # x_train_eli = rfecv.transform(x_train) # print(rfecv.estimator_.score(x_train_eli,y_train)) # print(rfecv.estimator_.score(x_test_eli,y_test)) # 数据预处理 # 数据分箱 # 上一步:数据预处理——缺失值、异常值、重复值处理 # 下一步:变量显著性检验——计算 WOE、IV # https://zhuanlan.zhihu.com/p/52312186 # from sklearn.preprocessing import KBinsDiscretizer # k = KBinsDiscretizer([5,6,7],encode='onehot-dense',strategy='uniform') # encode 离散化编码方式。分为 onehot,onehot-dense, ordinal # 具体分箱个数,是依据拟合的效果调试出来的。 # onehot 使用独热编码,返回稀疏矩阵 # onehot-dense 使用独热编码,返回稠密矩阵 # ordinal 使用序数编码(0,1,2,...) # strategy 分箱的方式 # uniform 每个分区的长度范围大致相同 # quantile 每个区间包含的元素格式大致相同 # kmeans 使用一维kmeans方式进行分箱 # discretize = ['Longitude','Latitude','Altitude'] # k.fit_transform(data[discretize]) # k.fit_transform(X_train) # 返回是二维数组,需转为DataFrame # k.transform(X_test) # 不能对测试机使用 fit_transform 方法
# k.transform() k.fit_transform() 都只传入一个参数。X # x_test_dis = pd.concat([x_test_eli.drop(discretize,axis=1),pd.DataFrame(res,index=x_test_eli.index)],
# axis=1) # 对处理完后的数据进行线性回归,看预测得分。 # lr.fit(x_train_dis,y_train) # lr.score(x_test_dis,y_test) # lr.score(x_train_dis,y_train) # 残差图分析 # 残差就是模型预测值与真实值之间的差异,残差图的横坐标为预测值,纵坐标为残差值。 # 残差图的应用 # 异方差性 # 离群点 # 多元线性回归,回归线已成为超平面,无法通过可视化来进行观察。 # 通过排除离群点,进一步优化线性模型 lr # y_hat_train = lr.predict(X_train_dis) # residual = y_hat_train - y_train.values # r = (residual - residual.mean()) / residual.std() # X_train_dis_filter = X_train_dis[np.abs(r) <=2] # y_train_filter = y_train[np.abs(r)<=2] # lr.fit(X_train_dis_filter,y_train_filter) # print(lr.score(X_train_dis_filter,y_train_filter)) # print(lr.score(X_test_dis,y_test)) # 超参数调整 # 备注:过程中可能重复进行多次操作,比如去除异常点。异常值可能会影响建模。这里采用的方式是临界值填充,当然肯定有其它方式。 # 数据可视化 # 选取合适的工具 # plt # seaborn # bokeh # 结论
# 机器学习 # one-hot encoding # https://blog.csdn.net/pipisorry/article/details/61193868 # 如果为“马”分配的索引是 1247,那么为了将“马”馈入到您的网络中,可以将第 1247 个输入节点设成 1,其余节点设成 0。这种表示法称为独热编码
# (one-hot encoding),因为只有一个索引具有非零值 # 一般来说,机器学习教程会推荐你或要求你,在开始拟合模型之前,先以特定的方式准备好数据。 # 其中,一个很好的例子就是对类别数据(Categorical data)进行 One-Hot 编码(又称独热编码) # 虚拟变量 # https://wiki.mbalib.com/wiki/%E8%99%9A%E6%8B%9F%E5%8F%98%E9%87%8F # 数据分箱 # 是一种数据预处理技术,用于减少次要观察误差的影响,是一种将多个连续值分组为较少数量的“分箱”的方法 # https://www.jianshu.com/p/0805f185ecdf # https://www.cnblogs.com/Christina-Notebook/p/10025470.html # 残差 # https://baike.baidu.com/item/%E6%AE%8B%E5%B7%AE # 残差在数理统计中是指实际观察值与估计值(拟合值)之间的差 # 在回归分析中,测定值与按回归方程预测的值之差,以δ表示。残差δ遵从正态分布N(0,σ2)。(δ-残差的均值)/残差的标准差,称为标准化残差,以δ*表示。
# δ*遵从标准正态分布N(0,1)。实验点的标准化残差落在(-2,2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2,2)区间以外,可在95%置信度将
# 其判为异常实验点,不参与回归直线拟合。 # 显然,有多少对数据,就有多少个残差。残差分析就是通过残差所提供的信息,分析出数据的可靠性、周期性或其它干扰。 # 残差图 # https://wiki.mbalib.com/wiki/%E6%AE%8B%E5%B7%AE%E5%9B%BE # 残差图的作用 # https://www.jianshu.com/p/c9022affd8b9 # https://blog.csdn.net/weixin_41500849/article/details/80372432 # 特征筛选 # 递归式特征消除:Recursive feature elimination # https://blog.csdn.net/FontThrone/article/details/79004874 # RFECV # FE的主要思想是反复构建模型(如SVM和回归)然后选出最好的或最差的特征,把选出来的特征放一边,然后在剩余的特征上重复过程,直到遍历所有特征。
# 这个过程中特征被消除的次序就是特征的排序。因此这是一种寻找最优特征子集的贪心算法。sklearn提供了RFECV,可以通过交叉验证来对特征进行排序 # 该函数返回一个调优后的模型,可以应用fit(), fit_transform(),predict()等等方法,还有诸如n_features_, support_, ranking_等属性。 # 这个模型会自动把传入的X修整为调优后数据的特征规格,然后再预测 # sns.heatmap(data,cmap,annot) # 热力图,属于 Matrix plots 。data 一般为数组。annot默认为false,设为True,会显示数值。 # 皮尔森系数 # 计算简单,应用广泛,适用于衡量变量之间的线性关系 # 由于公式的分母是变量的标准差,这就意味着计算皮尔森相关性系数时,变量的标准差不能为0(分母不能为0)。 # 也就是说你的两个变量中任何一个都不能没有波动。如果是常数,用皮尔森相关系数是没办法算出这两个变量之间是不是有相关性的 # 此外,实验数据通常假设是成对地来自于正态分布。因为我们在求皮尔森相关系数之后,通常还会用t检验之类的方法来进行皮尔森相关检验,而 t检验是基于
# 数据呈正态分布的假设的 # 而且实验数据之间的差距不能太大,或者说皮尔森相关性系数受异常值的影响比较大
# 差异检测 # stats.levene 方差齐性检测 # Perform Levene test for equal variances. # The Levene test tests the null hypothesis that all input samples are from populations with equal variances # 检验方差是否齐 stats.levene(coastal['AQI'],inline['AQI']) # Calculate the T-test for the means of *two independent* samples of scores. # This is a two-sided test for the null hypothesis that 2 independent samples # have identical average (expected) values. This test assumes that the # populations have identical variances by default. # 对于两个独立样本具有相同平均(预期)值的零假设,这是一个双侧检验 # 独立两样本t检验 stats.ttest_ind(inline['AQI'],coastal['AQI'])
# 混淆矩阵 # 混淆矩阵是对分类问题的预测结果的总结。使用计数值汇总正确和不正确预测的数量,并按每个类进行细分, # 这是混淆矩阵的关键所在。混淆矩阵显示了分类模型的在进行预测时会对哪一部分产生混淆。它不仅可以让您了解分类模型所犯的错误, # 更重要的是可以了解哪些错误类型正在发生。正是这种对结果的分解克服了仅使用分类准确率所带来的局限性。 from sklearn.metrics import confusion_matrix matrix = confusion_matrix(y_test,y_hat) plt.matshow(matrix,alpha=0.6,cmap='Blues') for i in range(matrix.shape[0]): for j in range(matrix.shape[1]): plt.text(i,j,matrix[i,j],va='center',ha='center')




