清北学堂培训整理7 13
今日wz来相会,相与坐在机房中
心中但念此客贵,忙请大佬入座中
不知触控何处关,大佬悠然敲键盘
重启过后猛然觉,博客未存车已翻
译文:关闭触控板重启以后发现博客没存
我尽量还原
补下昨天贪心:

看到这道题第一感觉就是让快的来回跑,送人就行
看下样例:

易证,如果让快的来回送(就是1),需要20分钟
然而这个17怎么来的?
考虑以下方案:
先让1和2过河,1回来送手电筒 3分钟
再让5和10过去,2回来送 12分钟
最后1和2过去 2分钟
共17分钟
看一看样例可得,如果只派最快的人来回跑,让他去接非常慢的人是一种浪费,
那么考虑让最慢的和次慢的去跑,这样可以不浪费最快的"才华"(才华缩写是CH)
所以这个其实是个动归?
1.最小带最大
\(dp_i=dp_{i-1}+a_i+a_1\)
2.最小带第2小,最小回来,最大2人过去,第二小回来
\(dp_i=dp_{i-2}+a_i+a_1+2a_2\)
所以就是这样的:
\(dp_i=min(dp_{i-1}+a_i+a_1,dp_{i-2}+a_i+a_1+2a_2)\)




数论
高精加
之前整过,代码好写,思路简单,不作整理
高精乘
之前整过,代码好写,思路简单,不作整理
高精减
之前整过,代码好写,思路简单,不作整理
高精除低精
之前整过,代码好写,思路简单,不作整理
高精除高精

先将位数对齐,然后从高位到低位进行比较,大了就除,小了这位是0
然后将被除数各位减去除数对应位数
当然在减的过程中需要处理借位
最后处理前导0
细节很多,慢慢看
高精开根

矩阵
首先声明1点:矩阵乘法所用的循环变量k在内层
我把这玩意记错了好久
快速幂
原理如普通快速幂,就是把*运算正确地重载运算符
然后一波乘,一波快速幂
这个东西可以用在矩阵加速上
矩阵加速
众所周知,矩阵(乘法,加速啥的)可以用来求数列第\(n\)相,鬼知道为什么
具体原理就是...
高斯消元
一个很重要的东西,
思路很简单,就是小学求二元一次方程组的道理
只是把它扩大了
理论给出阐述:
其目的就是消为一个这样的矩阵:
2 0 0 6
0 3 0 6
0 0 3 6
可以求n元方程的解
就是每次将第\(i\)行的第\(i-1\)项消为0
然后消成倒三角后再反着消回来
会了理论ta就是个dd简单模拟题
贴下代码:
#include<bits/stdc++.h>
using namespace std;
int n;
double a[105][105];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n+1;j++) scanf("%lf",&a[i][j]);
}
for(int i=1;i<=n;i++){
int t=i;
while(a[t][i]==0&&t<=n) t++;
if(t==n+1){
cout<<"No Solution";
return 0;
}
for(int j=1;j<=n+1;j++) swap(a[t][j],a[i][j]);
double x=a[i][i];
for(int j=1;j<=n+1;j++) a[i][j]/=x;
for(int j=1;j<=n;j++){
if(j==i) continue;
x=a[j][i];
for(int k=1;k<=n+1;k++){
a[j][k]-=x*a[i][k];
}
}
}
for(int i=1;i<=n;i++) printf("%0.2lf\n",a[i][n+1]);
return 0;
}
素数相关
真的不想整...
埃拉托瑟尼筛
之前整过,代码好写,思路简单,不作整理
线性筛
之前整过,代码好写,思路虽然不是那么很简单,但是不作整理
积性函数
之前没整这次好好听(说实话之前的博客太水了)


欧拉函数变式一下就是这样:
\(\phi(n)=\prod (p_i-1)p_i^{q_{i-1}}\)
\(\uparrow\)这个东西念\(f\breve a i\)
这个东西有两种可能:
1.\(gcd(i,p)=1\)
\(phi[i*p]=phi[i]*phi[p]\)
2.\(gcd(i,p)\neq1\)
\(phi[i*p]=phi[i]*p\)
这个东西可以在线性筛(欧拉筛)中顺带求出
顺带一提,莫比乌斯函数是完全积性函数
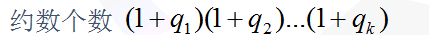
这个东西也是积性函数
这个东西本身是乘法原理
注意这里的\(q_i\)指的是指数\(p_i\)的次数
然后就考虑从\(k\)个物品中取物(可以不取),求方案数
因为不取也是一种方案,所以要+1
最 大 公 约 数
就是\(gcd\)!
我为啥这么高兴?
因为这个我能听懂!
朴素算法
之前没整过,但代码好写,思路简单,不作整理
辗转相除
之前整过,代码好写,思路简单,不作整理
原理不作解释,下面放一个二进制求\(gcd\)

这个东西因为只有位运算,比较快
BFS
这里的BFS并非\(breath\ first\ search\)
是\(best\ first\ seach\)
贪心搜索
然而其致命之处就是"不够聪明"
然后把这两个东西结合,
就是"启发式搜索"
这个东西其中变量的具体意义在下面

就是说,这种算法需要先估计优方案,然后如果发现再进行搜索

裴蜀定理

其实我早就选择背下来了...
这个可以求解不定方程

当然也可以线性求逆元...
代码:
#include<bits/stdc++.h>
using namespace std;
int n;
int p;
long long ans[3000005];
int main(){
int x,y;
scanf("%d%d",&n,&p);
ans[1]=1;
for(int i=2;i<=n;i++){
ans[i]=(long long)(p-p/i)*ans[p%i]%p;
printf("%lld\n",ans[i-1]);
}
printf("%lld\n",ans[n]);
return 0;
}



