清北学堂培训整理7 12

思想迟到了（装机呢），尽快赶上

今天培训最先开始讲了个模拟

模拟

本以为不用听，然而老师讲了下一些不得不听的东西

讲了一些代码习惯的养成

比如说码风

模拟考的是细心，是将人类语言转为的电脑语言的能力

而且模拟考的题一般代码都非常长

所以一边写对代码非常重要

这个对我真的太真实了

如果只向luogu无限调试一般在比赛拿不到分

所以力求一遍对

这种模拟题更强调的就是选手的代码能力

其特点就是：题目特烦，细节超多，代码极长

考验的全部都是选手写代码的基本功

1、写长代码不出错的能力；2、多方面周全地考虑问题的能力；

前者要求我们有一个良好的代码习惯，而后者则要求我们在做题时头脑有清晰的逻辑

总之,模拟不需要数据结构这种基础中中高难的东西

但是考察做题人的代码能力,读题和优化

如何将已知步骤让电脑读懂别调试完一片开门红

数据分治(也是模拟中讲的一部分)

这是很实用的东西，

考虑下前面数据\(n\leq10\)的时候进行特判

再大一点进行搜索,

最后试一试自己没怎么有信心的正解

当然除非你遇到一道数据范围极小的题或者能够直接写出正解的题

贪心

再次扯下原理

局部最优推知全局最优，就是每一步只走当前最优，

然后就能正解，前提是无后效性，就是下一步优不优要看自己，不看上面几步

具体思路？

大胆猜想，无需证明

突然想起旁边坐着一个贪心dalaolz

而且贪心一般带着其他算法标签，比如数学或者模拟

例题：

老题了，线段覆盖

思路就是按后端点排序，然后按前端点遍历，能放就放，不考虑前端点是否有序，可以保证解最优

因为排序时可以保证后端点从小到大，这里不考虑前端点的原因如下图：

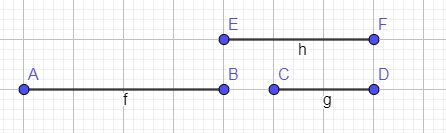
易知图中选择EF线段等价于选CD线段，因为都可以选且对于后面线段影响一致

于是我们巧妙地利用后端点的顺序间接考虑上了线段长度(两个后端点离得近,其中间的线段一定短)

另外一道题是伪蓝书(一本通提高)的例题,就是这张图:

思路就是把圆与矩形的交点(前后两个)视作是线段,然后进行线段覆盖

就完事了

上面的题没有贴代码,这题贴一个:

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
int read()
{
	char ch=getchar();
	int a=0,x=1;
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') x=-x;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		a=(a<<3)+(a<<1)+(ch-'0');
		ch=getchar();
	}
	return a*x;
}
int t,n,l,w;
int pos,R,ans,cnt;
struct water
{
	double l,r;
}a[15001];
int cmp(water x,water y)
{
	return x.l<y.l;
}
int main()
{
	t=read();
	for(int i=1;i<=t;i++)
	{
		n=read();
		l=read();
		w=read();
		cnt=0;
		for(int j=1;j<=n;j++)
		{
			pos=read();
			R=read();
			if(R<=w/2) continue;
			cnt++;
			a[cnt].l=pos-sqrt(R*R-(w/2.0)*(w/2.0));
			a[cnt].r=pos+sqrt(R*R-(w/2.0)*(w/2.0));
		}
		sort(a+1,a+1+cnt,cmp);
		double s=0,q;           //我们已经将区间覆盖了s米 
		int k=1,flag=0,ans=0;
		while(s<l)                       //覆盖不满就一直找喷水装置 
		{
			ans++;
			q=s;
			for(;a[k].l<=q&&k<=cnt;k++)    //在s左端找到一个右端点最大的值 
			   if(a[k].r>s) s=a[k].r;
			if(s==q&&s<l) {flag=1;cout<<0<<endl;break;}
		}
		if(flag==0) cout<<ans<<endl;
	}
	return 0;
}

另一道例题:

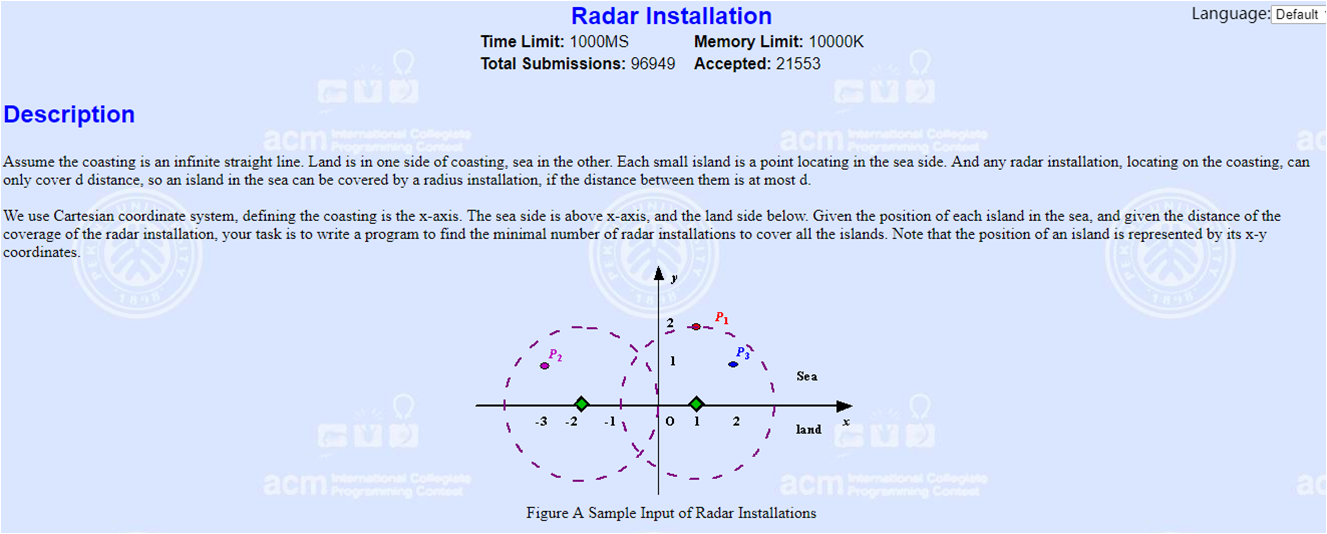
就是有\(n\)个点,给定半径\(d\)(半径是d???),求覆盖所有点的最小数量

一看题就能想到基本思路

把每个海岛处理成线段,进行覆盖,

这里因为线段表示的是可接受雷达放置的范围,即只要把雷达放在线段上就一定覆盖线段所属海岛

那么只要把雷达 放在线段密集的地方就是了

(当然第一步是排序)就是每次在考虑大线段时回到其能够包含(或重叠)的小线段,这是考虑"线段密集"这个思路的具体实现

等我A了把代码放上

---

切菜题警告
这题其实还有另一种贪心做法
这种思路简单的多
就是按照后端点排序后,每次只考虑在后端点放雷(达)
然后遍历一遍,如果这个点能够同时对其他线段起到贡献作用(就是能够在这个线段上)
那么就把这些线段标记一下,
以后再遍历到就可以忽略
代码:

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
int n,d;
struct node{
	double l,r;
}ed[1005];
inline double dis(const int &y){
	return sqrt((double)((1.0*d*d)-(1.0*y*y)));
}
inline bool cmp(const node &a,const node &b){
	return a.r<b.r;
}
bool vis[1005];
int main(){
	scanf("%d%d",&n,&d);
	for(int i=1;i<=n;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		if(y>d){
			printf("-1\n");
			return 0;
		}double len=dis(y);
		ed[i].l=x-len;
		ed[i].r=x+len;
	}
	sort(ed+1,ed+1+n,cmp);
	int ans=0;
	for(int i=1;i<=n;i++)
		if(!vis[i]){
			vis[i]=1;
			ans++;
			for(int j=1;j<=n;j++)
				if(!vis[j]&&ed[j].l<=ed[i].r)
					vis[j]=1;
		}
	printf("%d",ans);
	return 0;
}

打怪题:

排排序(杀完能回血的顺序按照消耗排序,不然按照回血降序,使扣血越来越多),回回血(先打目前实力能够打的并且回血的(回血指的是扣血\(\leq\) 回血)),扣扣血(再打能打但不能回血的),完成

注意这题需要倒序看,以保证不死

这么说的话可以dfs啊(滑稽