引水入城

最近在搞提高组的题,这是某天早上给的T1

T1最难还行

原题目

最近考试考多了就是见题打暴力,打搜索,

然而这题真是搜索,

但是并不能只搜索,会T,没亲测,但一定有效

这并不是考试题,所以看看标签(理直气壮的理由)

是BFS啊...

那就用DFS吧

这里的DP一开始看没有什么感觉,但是做着做着发现就是不应该有感觉,这是搜索+贪心啊

下面开始正式题解

首先明白一点,同一个水源可以有不同的目的地,而不同的目的地也可以有着不同的水源,由于这题要求看最少源头或是未通水的目的地数目,所以要对每个水源进行深搜,对能够通水的最后一行的格子进行标记

在来证明一个东西:

不存在源头\(a\)在\(b\)左边,但是\(a\)到达的区间在\(b\)所到达的右边,

就像这个图(无视那个\(S_1\)):

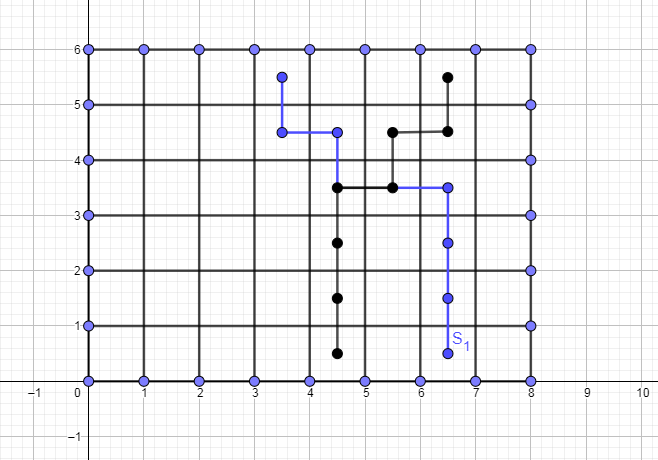
这个图很明显存在交叉,然而如果两个水源能够到达同一格,那么这个格所能够到达的所有下面的点这两个源头一定都能达到,并不存在交叉非公共部分

那么是否所有的搜索方式都不用网上搜呢?

你考虑这样一种路径就好了(灵魂手绘):

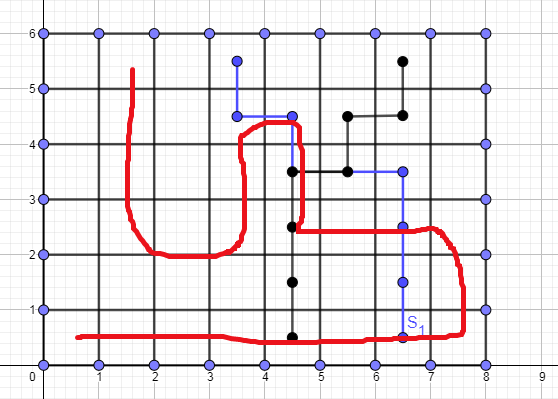
注意在进行vis数组标记时,所记录的到过的点只对本次搜索生效,也就是说,本次搜索搜到过的点待会可能别的点也要搜,并且搜到的区间也许更大,这对结构有着更大贡献,,如果因搜到过而停止搜索,会导致代码输出大部分大于答案,所以每次搜索到最后一层是需要用该点的表示列的坐标(由于横纵坐标与本题x,y在本题搞得有点昏,暂且这样称呼,有兴趣自己推吧)对该水源的左右区间端点进行更新

然后处理出每个水源能够到的最左端与最右端,

首先跑一遍最后一列,看有没有最后一行没有到达的格子如果有就是无解,在遍历时统计数量输出即可,

如果全部到达,则用sort函数(按左端点)排一下,并且每次去最长的线段,就是右端点最靠后的线段,当然前提是满足左端点小于上一条线段的右端点(对于第一条线段,其左边的限制是1)

每次将下一条线段的左端点限制更新为r+1,意义自证,

对于每个水源的区间更新,给出以下公式:

\(l_i=min(l_i,y)\)

\(r_i=max(r_i,y)\)

就是对于每个水源\(i\),用每个到达的最后一行的格子列坐标进行更新,当然要的是最左边的\(l\)和最右边的\(r\),分别用\(min\)函数和\(max\)函数取区间

当然,初始化时要把\(l\)赋值成\(inf\)(无穷大),把\(r\)赋值成\(-inf\),来保证区间更新操作的稳定

代码如下:

#include<bits/stdc++.h>
using namespace std;
#define R register
const int inf=0x3f3f3f3f;
int n,m;
int pos[505][505];
struct node{
	int l,r;
	node(){
		l=inf;
		r=-inf;
	}
}nd[505];
int mx[6]={0,-1,0,1,0};
int my[6]={0,0,1,0,-1};
bool vis[505][505],final[505];
inline void search(const int &x,const int &y,const int &p){
	vis[x][y]=1;
	if(x==n){
		final[y]=1;
		nd[p].l=min(nd[p].l,y);
		nd[p].r=max(nd[p].r,y);
	}
	for(R int i=1;i<=4;i++){
		int nx=x+mx[i];
		int ny=y+my[i];
		if(1<=nx&&nx<=n&&1<=ny&&ny<=m&&(!vis[nx][ny])&&(pos[x][y]>pos[nx][ny]))
			search(nx,ny,p);
	}
}
inline bool cmp(const node &a,const node &b){
	if(a.l!=b.l) return a.l<b.l;
	return a.r<b.r;
}
int main(){
	scanf("%d%d",&n,&m);
	for(R int i=1;i<=n;i++)
		for(R int j=1;j<=m;j++)
			scanf("%d",&pos[i][j]);
	for(R int i=1;i<=m;i++)
		if(pos[1][i-1]<=pos[1][i]&&pos[1][i]>=pos[1][i+1]){
			memset(vis,0,sizeof vis);
			search(1,i,i);
		}
	int tot=0;
	for(R int i=1;i<=m;i++)
		if(!final[i]) tot++;
	if(tot){
		printf("0\n%d",tot);
		return 0;
	}
	int num=0;
	for(R int i=1;i<=m;i++)
		if(nd[i].l!=inf&&nd[i].r!=-inf){
			nd[++num].l=nd[i].l;
			nd[num].r=nd[i].r;
		}
	sort(nd+1,nd+1+num,cmp);
	for(R int l=1,r=0,j=1;l<=m;l=r+1,r=0,tot++){
		while(nd[j].l<=l){
			r=max(r,nd[j].r);
			j++;
		}
	}
	printf("1\n%d",tot);
	return 0;
}