树状数组基础模板

树状数组是可用于求区间和并支持单点修改的高效数据结构,
在讲树状数组时往往有这样一张图:

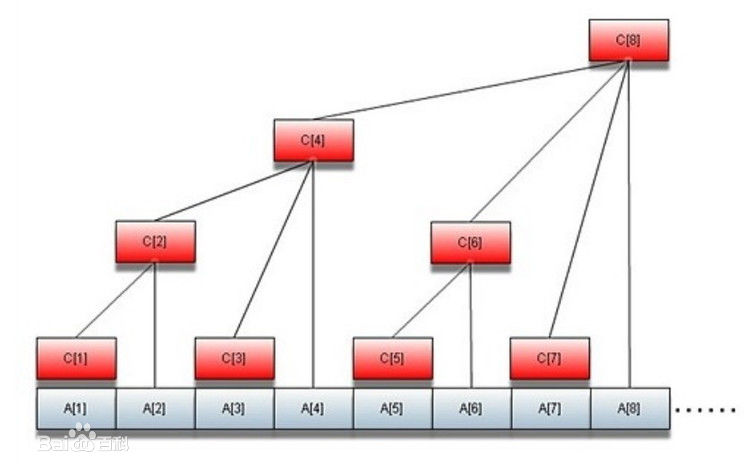
看上去非常恶心,也很难以理解(稍加理解却不知如何实现)...
然而ta的代码非常简短,起码作为一道板子题,ta是非常图样图森破辣...
众所周知,求前缀和的朴素算法思路无比简单,其代码就像这样:

int sum[233];
int a[233];  //everything is '0'
...          //something like read
for(int i=1;i<=100;i++){
	sum[i]=sum[i-1]+a[i];
}

p.s.最近写中文注释爆炸了(乱码),然后改用英语小文章了
由以上代码知,这个朴素算法非常暴力,并不能支持修改操作,修改就TLE,
现在用树状数组这样一种数据结构,将特定的元素归纳到一定的集合中,这样一来单点修改是就可以只修改包含该元素的节点,效率高不少
具体是怎么实现的呢?
树状数组是基于"数的2进制的唯一分解性质"的数据结构,
上面那个性质就是每个数所表示的二进制数是不同的,正确性自己证明
基于这个性质,一个\(1\simx\)的区间可以表示成\(log_2 x\)个小区间
长度都可表示为\(2^n\),
举个例子(举蓝书上的):
\(x=(21)_{10}=(10101)_{2}\)
\(len=2^4->1\sim(2^4)\)
\(len=2^2->(2^4+1)\sim(2^4+2^2)\)
\(len=2^0->(2^4+2^2+1)\sim(2^4+2^2+2^0)\)
由此可见,每个区间长度为二进制分解下最低位的2次幂
那么可以考虑用其进行区间之间的转换,
先考虑如何求其值
现在要求最低位的2次幂及更低位0所组成的数,
现在考虑这样一个二进制数:
其某一位为1,更低位全部为0,
那么将其取反,0变成1,1变成0
那么这一位原来是最低的1变成了0,后面变成了1,
再给它的反码+1,使最后我们要求的几位与原数一模一样,此时取一个&,就可以取得其值
而数\(n\)的反码为\(n-1\),那么所要求的\(lowbit\)就是\(n\& -n\)
这就是\(lowbit\)的求法,
而上面图片中的c数组就是基于其上的树形结构,其中元素满足以下性质:
1.对于其内部节点,都表示的是以其为根叶节点的和,注意这里是叶节点,不是所有编号小于等于其角标的元素(不然就成前缀和了)
2.每个节点的子节点个数等于\(lowbit(**ta的角标**)\)其实就是区间长度
3.非根节点的父亲角标一定是\(x+lowbit(x)\)
那么有了父与子的关系,就方便多了嘛...
先不说每个函数及其实现,先按题的流程来走一遍当然读入输出就...
首先建树(状数组),将每个读入的点加入,并对其祖宗进行维护,就是把ta家长都"家访"一遍,把该节点的值加给家长
读入完成时可以保证对应节点值的正确性,
在此声明一下
这里的家长节点只含其树状结构中的子节点,并不是ta之前的元素都含
也就是说,我们在区间求和时(基础树状数组好像只能求区间为\(1\sim n\)的前缀和)会将区间看成小区间,然后分别将其包含的节点加起来组成前缀和,不重复,不遗漏这TM分治???
建树完成之后,可以进行\(m\)次操作了,就是单点修改和区间查询,
对于单点修改,可以重复与建树一样的步骤
其实建树用的是单点修改的函数,因为二者互通,
对于建树,或称单点修改函数的实现及原理在上面已经给出证明与解析(其实我知道我是给了的,但是我混乱而混蛋地忘了写在哪里了...)
对于区间查询,就是对于任意左端点(\(l\))和右端点(\(r\)),先求出\(sum(r)\),再求出\(sum(l-1)\),相减即得答案,
区间查询函数的原理就是上面提到的树状数组"分治法"
(这好像就是单点修改正确性证明哦...)
即每次通过\(lowbit\)函数来将个个小区间联系起来(这就是\(for\)循环枚举时的循环变量变化操作),将遍历到的子节点全部相加,函数返回其总和值,这就是区间\(1\sim n\)的和,同样按照上述步骤求得左端点(当然要减去1,这样才是完整的需查询区间)为区间的总和...不再重复阐述步骤嘿!又水一行(滑稽)
这就是树状数组的理论依据(可能有表述不清),代码实现如下:

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
inline int lowbit(const int &n){
	return (n)&(-n);
}
int n;
int a[500005],c[2000005];
inline void add(const int &x,const int &y){
	for(int i=x;i<=n;i+=lowbit(i))
		c[i]+=y;
}
inline int sum(const int &x){
	int ans=0;
	for(int i=x;i;i-=lowbit(i)){
		ans+=c[i];
	}
	return ans;
}
int m;
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		add(i,a[i]);
	}
	while(m--){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		if(a==1)
			add(b,c);
		else
			printf("%d\n",sum(c)-sum(b-1));
	}return 0;
}

依旧是这样令人喜爱的码风呢