考试T1总结（又CE？！）

考试T1CE...

最近不适合考试

T1

扶苏是个喜欢一边听古风歌一边写数学题的人，所以这道题其实是五三原题。
歌曲中的主人公看着墙边的海棠花，想起当年他其实和自己沿着墙边种了一排海
棠，但是如今都已枯萎，只剩下那一株，寄托着对他深深的思念。
沿着墙一共有 n 个位置可以种下海棠花，主人公记得自己当年和他一共种下了 m
朵，由于花的特性，海棠不能紧挨着种植，也就是两朵海棠花之间最少间隔一个不种花
的空位置。但是她记不清当时海棠花具体是怎么摆放的了，所以她想知道一共有多少方
案使得 m 朵海棠花都被种下且两两之间不是相邻的。我们将这 m 朵海棠花按照
1,2,3…m 的顺序编号，两个种花的方案不同当且仅当它们被种下的位置不同或者从左向
右数花的编号序列不同。
为了避免输出过大，答案对一个参数 p 取模

这道题一看就是DP嘛...

是个数学题

就是有n个位置，m个不同物品，问m个物品都不相邻的摆法有几种，其中m小于ceil(n/2)，就是n/2上取整
思路分析：

思路一：

骗分输出最小的良心防爆零样例

思路二：

打神搜，其实T2，T3也可以这样操作，时间不够了...只拿了十分

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef unsigned int ui;
ui type,n,m,p;
inline ui arr(const ui &k){
    ui ans=1;
    for(ui i=2;i<=k;i++)
        ans=(ans*(i%p))%p;
    return ans;
}
int ans;
inline void search(const int &step,const int &pos){
    if(step==m){
        ans++;
        return;
    }
    for(int i=2;i<=n;i++){
        if(pos+i<=n&&step+1<=m)   //没有上下界剪枝
        search(step+1,pos+i);
    }
}
int main(){
    freopen("ilove.in","r",stdin);
    freoprn("ilove.out","w",stdout);    //大家注意这一行的freopen!!!!!!（目力呐喊！！！）
    scanf("%d%d%d%d",&type,&n,&m,&p);
    for(int i=1;i<=n-(m-1)*2;i++) //遍历每个可能的点找可能的路线，所以非常慢，只能处理范围在20以内的点
        search(1,i);
    cout<<ans*arr(m);
    return 0;
}

思路三（正经思路）：

一开始的思路是考虑n个位置选m个位置再减去相邻情况，然而这并不好代码实现，而且最大数据范围是n<=2000000，m<=1000000，然而组合数最广为人知的求法要么是前缀和（杨辉三角），要么是公式计算，

前缀和算法会因为数据范围而时间爆炸，公式计算因为取模运算的存在而正确性爆炸...

双倍爆炸，双倍快乐，算法两开花！！！

前缀和的爆炸原因不解释，有目共睹...

下面讲下关于组合数取模的错误的原因：

现给出组合数计算公式（并不想百度百科...）：

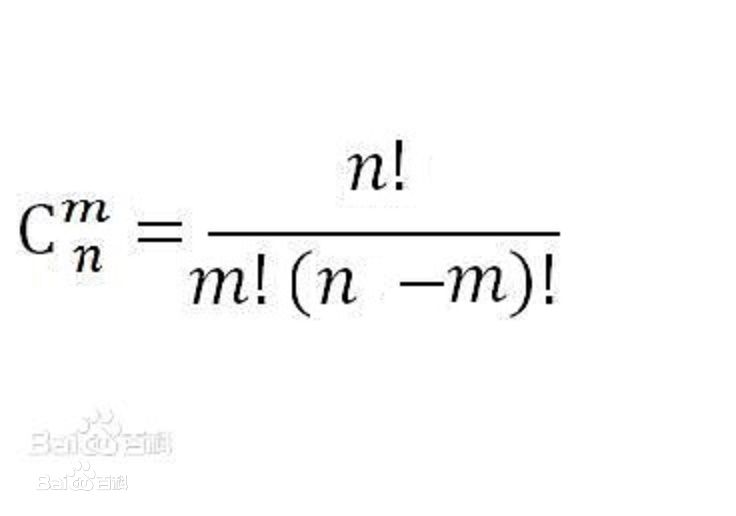
本式值即为在n个互不相同的东西中取m个的方案总数

并且可以直观的看出该值的直接公式运算需要除法的参与，

已知四则运算中的加减乘满足“一边算一边模还保证正确性”定律（瞎起的名字）

除可不可以？

那么现在考虑如下式子：

15/21 (mod 20)

15/7   (mod 3)

14/6   (mod 3)

如果把分子分母分别进行模运算再除，得到的值显然不正确，

那么现在就要考虑乘法逆元了

整除也不行（考虑15/5 （mod 7））

所以要么把乘法逆元板子搬过来，要么就把运算全都变成乘运算

现在考虑推一个保证正确的式子再将其尽可能的化简

现有m个不同物品摆在n个位子，那么就有n-m个空位

现在保证正确的方案就是把这几个空位固定，在它们之间插空摆物品，以保证每两个物品之间至少有一个空位

如图：

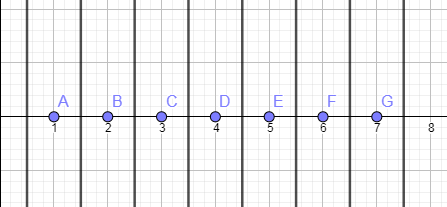
每两点的中间（包括最边上的两点之外那两条线）就是合法方案的可选位置

那么就是n-m+1个位置中选择m个位置摆物品，在考虑物品的排列顺序就好了

就是这样：

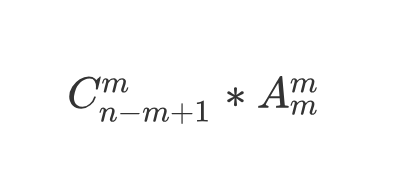
又知：

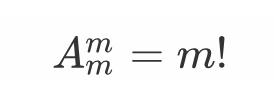
辣么它们的乘机化简下，就是这样滴：

那么剩下的只有乘法运算辣！

最后说一点，由于模数最大好像是10⁹，所以要开long long，并且由于本题经过分析后数据范围就相当于很小了，所以不用专门写函数加上inline加速，根本没必要...

代码（及其简短）：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
long long n,m,p;
long long type;  //当时type为什么要开long long
int main(){
    scanf("%d%d%d%d",&type,&n,&m,&p);   //type变量用来判别测试点类型（骗分的）
    long long ans=1;
    for(int i=n-2*m+2;i<=n-m+1;i++)
        ans=ans*i%p;
    printf("%d\n",ans);
    return 0;
}