测试总结
今后将有大量试题与博客出没(想回去中考。。。)
T1:
FBI树
我们可以把由“0”和“1”组成的字符串分为三类:全“0”串称为B串,全“1”串称为I串,既含“0”又含“1”的串则称为F串。
FBI树是一种二叉树,它的结点类型也包括F结点,B结点和I结点三种。由一个长度为2^N的“01”串S可以构造出一棵FBI树T,递归的构造方法如下:
1) T的根结点为R,其类型与串S的类型相同;
2) 若串S的长度大于1,将串S从中间分开,分为等长的左右子串S1和S2;由左子串S1构造R的左子树T1,由右子串S2构造R的右子树T2。
现在给定一个长度为2^N的“01”串,请用上述构造方法构造出一棵FBI树,并输出它的后序遍历序列。
看上去很麻烦,实际上就是根据原字符串进行处理,每次将字符串从中间分为两等长字符串,再分别判断类型
结合代码讲下:
1 #include<iostream> 2 #include<cstdio> 3 #include<queue> 4 #include<algorithm> 5 #include<cstring> 6 #include<string> 7 using namespace std; 8 int n; 9 struct node{ //其中数组大小很鬼畜,一开始大小为1024左右,然而RE,就开了十倍大小,luogu过了 10 int size; 11 char a[10300]; 12 char type; 13 }nd[10240]; 14 int po(int k){ //快速幂,其实用pow好像慢不了多少,因为本函数在本题中并不常用 15 int t=2; 16 int p=1; 17 while(k){ 18 if(k&1) 19 p*=t; 20 t*=t; 21 k>>=1; 22 } 23 return p; 24 } 25 inline void search(int numb,int de){ //因为用的特别多,加了inline,递归处理字符串 26 int l=numb*2; //根据满二叉树的节点编号特征将节点编号表示出来 27 int r=numb*2+1; 28 nd[l].size=nd[numb].size/2; 29 nd[r].size=nd[numb].size/2; 30 for(int i=0;i<nd[numb*2].size;i++){ 31 nd[l].a[i]=nd[numb].a[i]; 32 nd[r].a[i]=nd[numb].a[i+nd[l].size]; 33 } //一人一半 34 bool ok1=0,ok0=0; 35 for(int i=0;i<nd[l].size;i++){ //遍历判断字符串类型 36 if(nd[l].a[i]=='1') 37 ok1=1; 38 if(nd[l].a[i]=='0') 39 ok0=1; 40 if(ok1&&ok0) 41 nd[l].type='F'; 42 else if(!ok1) 43 nd[l].type='B'; 44 else if(!ok0) 45 nd[l].type='I'; 46 } 47 ok1=0;ok0=0; 48 for(int i=0;i<nd[r].size;i++){ 49 if(nd[r].a[i]=='1') 50 ok1=1; 51 if(nd[r].a[i]=='0') 52 ok0=1; 53 if(ok1&&ok0) 54 nd[r].type='F'; 55 else if(!ok1) 56 nd[r].type='B'; 57 else if(!ok0) 58 nd[r].type='I'; 59 } 60 if(de==n+1) return; //处理完毕的边界条件 61 else{ //递归处理 62 search(l,de+1); 63 search(r,de+1); 64 } 65 } 66 //<-编号鬼畜了
67 void print(int numb){ //后序输出,也是递归 68 if(numb>po(n+1)-1) return; 69 print(numb*2); 70 print(numb*2+1); 71 putchar(nd[numb].type); 72 } 73 int main(){ 74 //freopen("fbi.in","r",stdin); 75 //freopen("fbi.out","w",stdout); 76 scanf("%d",&n); 77 scanf("%s",nd[1].a); 78 nd[1].size=po(n); 79 bool ok1,ok0; 80 for(int i=0;i<nd[1].size;i++){ //判断原字符串 81 if(nd[1].a[i]=='1') 82 ok1=1; 83 if(nd[1].a[i]=='0') 84 ok0=1; 85 if(ok1&&ok0) 86 nd[1].type='F'; 87 else if(!ok1) 88 nd[1].type='B'; 89 else if(!ok0) 90 nd[1].type='I'; 91 } 92 search(1,1);/* 93 for(int i=1;i<=15;i++){ 94 cout<<nd[i].size<<endl; 95 for(int j=0;j<nd[i].size;j++) 96 cout<<nd[i].a[j]; 97 cout<<endl; 98 cout<<nd[i].type<<endl; 99 cout<<endl; 100 } 调试用的*/ 101 print(1); 102 return 0; 103 }
这回显示行号以示友好...
本题很简单,然而本机测试无伤,手动测试无伤,lemon测试不过???丢了10分,导致掉了3名
那个数据还是不属于数据范围的...
T2:
医院设置
设有一棵二叉树,如图:
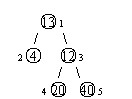
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为1。如上图中,
若医院建在1 处,则距离和=4+12+2*20+2*40=136;若医院建在3 处,则距离和=4*2+13+20+40=81……
就是求路程最小情况的总路程
乍一看:又是树?LCA?
看看luogu标签(当然我是刚刚(考试后)看的):


到底是啥?
一琢磨就知道这好像是最短路问题,看看可爱的数据范围:
第一行一个整数n,表示树的结点数。(n≤100)
n3好像没问题
就是用Floyd
代码(5分钟的产品...):
#include<iostream> #include<cstdio> #include<queue> #include<algorithm> #include<string> #include<cstring> using namespace std; int n; int peo[105]; int dis[105][105]; int main(){ //freopen("hospital.in","r",stdin); //freopen("hospital.out","w",stdout); memset(dis,0x3f,sizeof(dis)); scanf("%d",&n); for(int i=1;i<=n;i++) dis[i][i]=0; for(int i=1;i<=n;i++){ int a,b; scanf("%d%d%d",&peo[i],&a,&b); if(a!=0){ dis[i][a]=1; dis[a][i]=1; } if(b!=0){ dis[i][b]=1; dis[b][i]=1; } } for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(dis[i][j]>dis[i][k]+dis[k][j]){ dis[i][j]=dis[i][k]+dis[k][j]; dis[j][i]=dis[i][k]+dis[k][j]; } int minn=2147483647; for(int i=1;i<=n;i++){ int sum=0; for(int j=1;j<=n;j++){ sum+=peo[j]*dis[i][j]; } minn=min(minn,sum); } cout<<minn; return 0; }
Floyd模板加枚举暴力,不解释...
T3:
加分二叉树
设一个nn个节点的二叉树tree的中序遍历为(1,2,3,…,n1,2,3,…,n),其中数字1,2,3,…,n1,2,3,…,n为节点编号。每个节点都有一个分数(均为正整数),记第ii个节点的分数为di,treedi,tree及它的每个子树都有一个加分,任一棵子树subtreesubtree(也包含treetree本身)的加分计算方法如下:
subtreesubtree的左子树的加分× subtreesubtree的右子树的加分+subtreesubtree的根的分数。
若某个子树为空,规定其加分为11,叶子的加分就是叶节点本身的分数。不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n1,2,3,…,n)且加分最高的二叉树treetree。要求输出;
(1)treetree的最高加分
(2)treetree的前序遍历
这个题看似难,
实际确实很难
最常见的解法就是区间dp和记忆化搜索(都不会)
代码:
#include<iostream> #include<cstdio> using namespace std; int n; long long dp[35][35]; //注意,和有可能大于231,用dp_i_j表示从i——j最大情况 int rt[35][35]; int a[35]; void print(int l, int r) { //同T1递归处理 if(l>r)return; if(l==r){ printf("%d ",l); return; } printf("%d ",rt[l][r]); print(l,rt[l][r]-1); print(rt[l][r]+1,r); } int main(){ //freopen("binary.in","r",stdin); //freopen("binary.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); dp[i][i]=a[i]; dp[i][i-1]=1; //处理这里的目的是接下来有可能k=i,此时无右子树,所以需将其处理为1 rt[i][i]=i; } for(int len=2;len<=n;len++){ //枚举区间,即需处理范围 for(int i=1;i<=n-len+1;i++){ int j=i+len-1; for(int k=i;k<=j;k++){ //枚举根结点 if(!dp[k+1][j]) dp[k+1][j]=1; //将空区间设为1 if(!dp[i][k])dp[i][k]=1; if(dp[i][k-1]*dp[k+1][j]+a[k]>dp[i][j]){ dp[i][j]=dp[i][k-1]*dp[k+1][j]+a[k]; //状态转移,找到最优方案将其保存 rt[i][j]=k; //此处不用max()函数因为还要判断保存根结点 } } } } cout<<dp[1][n]<<endl; print(1,n); return 0; }
由题意可知,要求的最大加分即为左右两子树乘积加根结点,所以dp方程如下:
dp[i][j]=max(dp[i][k-1]*dp[k+1][j]+a[k])
同时进行根的保存,用于输出前序遍历,此处rt[i][j]指的从i——j加分最大子树的根结点,方便递归处理,
最后输出全局结果,就是把整个树的情况输出,dp[1][n]显然指从1——n结点成树最大情况,而print 1——n指的是将刚刚1——n结点成树的图输出



