「NOIP第四阶段」整理
模拟赛45

考试时犯困,T3暴力都没打
T1: bins
一眼沙雕题,指针+桶扫一遍就行了
T2:inversions
归并没学两行泪
由于没学归并,考场就没往正解上想
考虑一个区间翻转对其它区间的影响
-
对本级及含于本级的区间,逆序对个数与正序对个数交换
-
对于同级其他及本级以上,当前区间没影响
所以直接用归并统计出每一级区间的正逆序对个数,修改时打标记即可
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define rint register int
#define ll long long
#define ull unsigned long long
#define Max(a,b) (a>b?a:b)
using namespace std;
const int maxn=1e6+5e5+5,INF=0x3f3f3f3f;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s*w;
}
ull k1,k2;
int a[maxn],q[maxn],flag;
inline ull xorShift128Plus(){
ull k3=k1,k4=k2;
k1=k4;
k3^=(k3<<23);
k2=k3^k4^(k3>>17)^(k4>>26);
return k2+k4;
}
int n,m,threshold,b[maxn],c[maxn];
bool vis[maxn];
ll ans,now,f[22],g[22];
#define mid ((l+r)>>1)
void merge_sort(int l,int r){
if(l==r)return;
merge_sort(l,mid);merge_sort(mid+1,r);
int idl=l,idr=mid+1,id=l-1,now=log2(r-l+1);
while(idl<=mid&&idr<=r){
if(a[idl]<=a[idr]){
b[++id]=a[idl];
idl++;
}else{
b[++id]=a[idr];
if(flag==1)g[now]+=mid-idl+1;
else f[now]+=mid-idl+1;
idr++;
}
}
while(idl<=mid)b[++id]=a[idl++];
while(idr<=r)b[++id]=a[idr++];
for(id=l;id<=r;++id)a[id]=b[id];
}
signed main(){
freopen("inversions.in","r",stdin);
freopen("inversions.out","w",stdout);
n=read(),m=read(),threshold=read(),cin>>k1>>k2;
int maxs=1<<n;
for(rint i=1;i<=maxs;++i)a[i]=xorShift128Plus()%threshold+1;
for(rint i=1;i<=m;++i)q[i]=xorShift128Plus()%(n+1);
n=(1<<n);
memcpy(c,a,sizeof(a));flag=1;
merge_sort(1,n);
memcpy(a,c,sizeof(c));flag=2;
reverse(a+1,a+1+n);
merge_sort(1,n);
n=log2(n);
for(rint i=1;i<=m;++i){
ll now=0;
for(rint j=1;j<=n;++j){
if(j<=q[i])vis[j]^=1;
if(vis[j])now+=f[j];//,cout<<f[j]<<" ";
else now+=g[j];//,cout<<g[j]<<" ";
}
ans^=(now*i);
}
printf("%lld\n",ans);
return 0;
}
T3:candies
送的50pts没打,awsl
第一问相当于消失之物,考场忘了消失之物咋写硬搞还搞错了
具体点,取 \(q\) 为 正无限,那当前能表示的数就可以翻倍
所以直接消失之物找最多表示
第二问就有。意思了,
对于不合法的 \(q\) ,显然有
\[S + q = T (S,T均为可表示的集合)
\]
移项
\[q = T - S
\]
发现就是一个权值可正可负的背包,所以再跑一遍背包找出最大不能表示的数
负下标写法是从liu_run_da某篇题解里学的
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define rint register int
#define ll long long
#define ull unsigned long long
#define Max(a,b) (a>b?a:b)
using namespace std;
const int maxn=7e5+5,INF=0x3f3f3f3f,mol=1e9+7,base=7e5;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s*w;
}
int DP[maxn*2],f1[maxn],maxid,ans,a[maxn],n,sum,f3[maxn],sum1[maxn];
int *f2=DP+base;
int main(){
freopen("candies.in","r",stdin);
freopen("candies.out","w",stdout);
n=read();
for(rint i=1;i<=n;++i)a[i]=read(),sum+=a[i];
sort(a+1,a+1+n);
f1[0]=1;
for(rint i=1;i<=n;++i){
for(rint j=sum;j>=a[i];--j){
f1[j]+=f1[j-a[i]];
if(f1[j]>mol)f1[j]-=mol;
}
}
sum1[0]=1;
for(rint i=1;i<=sum;++i)sum1[i]=sum1[i-1]+(f1[i]>=1);
memcpy(f3,f1,sizeof(f1));
for(rint i=1;i<=n;++i){
for(rint j=0;j<=sum;++j)f1[j]=f3[j];
int cnt=sum1[a[i]-1];
for(rint j=a[i];j<=sum;++j){
if(f1[j-a[i]]){
f1[j]-=f1[j-a[i]];
if(f1[j]<0)f1[j]+=mol;
}
if(f1[j])cnt++;
}
if(cnt>ans)ans=cnt,maxid=i;
}
printf("%d ",a[maxid]);
f2[0]=1;
for(rint i=1;i<=n;++i){
if(i==maxid)continue;
for(rint j=sum;j>=-sum;--j){
if(j-a[i]>=-sum)f2[j]|=f2[j-a[i]];
}
for(rint j=-sum;j<=sum;++j){
if(j+a[i]<=sum)f2[j]|=f2[j+a[i]];
}
}
for(rint j=0;j<=sum+a[maxid]+1;++j){
if(!f2[j]){printf("%d\n",j);break;}
}
return 0;
}
T4:sheep
傻逼题给爷爬
晚间小测10

T1:跳跃
前几天刚考过的折半枚举
发现折半后的一个状态合法有两个条件:
-
\(w1 + w2 >= m\)
-
前一半尾位不大于后一半首位
前一半直接排序,后一半对每一个首位存状态,vector内部按权值排序,再记录一个指针
由于合法状态一定不满,空间最大不会超过64MB
另外没事少开 #define int long long(指某人MLE了)
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define rint register int
#define ll long long
#define Max(a,b) (a>b?a:b)
#define Min(a,b) (a<b?a:b)
const int maxn=1e6+5e5+5,INF=0x3f3f3f3f;
using namespace std;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s*w;
}
int n,a[45],b[45],id[45],tot,tot1;
ll m,ans;
struct Node{
int s,x;
ll w;
bool operator <(const Node &A)const{
return w==A.w?x<A.x:w<A.w;
}
}q1[maxn];
struct Nodee{
int s,x;
ll w;
Nodee(int _s,int _x,ll _w){s=_s,x=_x,w=_w;}
bool operator <(const Nodee &A)const{
return w==A.w?x<A.x:w<A.w;
}
};
vector<Nodee> g[45];
int main(){
freopen("san.in","r",stdin);
freopen("san.out","w",stdout);
n=read();scanf("%lld",&m);
for(rint i=1;i<=n;++i)a[i]=read(),b[i]=read();
int siz=n/2,maxs1=(1<<siz)-1,maxs2=(1<<n-siz)-1,now;
ll sum;
for(rint s=1;s<=maxs1;++s){
now=0;sum=0;
int last=0;
for(rint i=1;i<=siz;++i){
if(s&(1<<i-1)){
if(a[i]<now)goto skr1;
now=a[i];
sum+=1LL*b[i];
last=i;
}
}
if(sum>=m)ans++;
q1[++tot1]=(Node){s,last,sum};
skr1:;
}
for(rint s=1;s<=maxs2;++s){
now=0;sum=0;
int fst=0;
for(rint i=1;i<=n-siz;++i){
if(s&(1<<i-1)){
if(!fst)fst=i;
if(a[i+siz]<now)goto skr2;
now=a[i+siz];
sum+=1LL*b[i+siz];
}
}
if(sum>=m)ans++;
g[fst].push_back(Nodee(s,fst,sum));
skr2:;
}
sort(q1+1,q1+1+tot1);
for(rint i=1;i<=n-siz;++i){
sort(g[i].begin(),g[i].end());
id[i]=g[i].size();
// for(rint j=0;j<g[i].size();++j)cout<<i<<" "<<g[i][j].w<<" "<<g[i][j].x<<endl;
}
for(rint i=1;i<=tot1;++i){
for(rint j=1;j<=n-siz;++j){
if(a[j+siz]<a[q1[i].x]||g[j].empty())continue;
while(id[j]&&g[j][id[j]-1].w+q1[i].w>=m)id[j]--;
//cout<<i<<" "<<j<<" "<<id[j]<<" "<<g[j].size()<<" "<<ans<<endl;
ans+=(int)g[j].size()-id[j];
// cout<<i<<" "<<q1[i].x<<" "<<g[j][id[j]].w<<" j="<<j<<" "<<id[j]<<" "<<g[j].size()<<" ans="<<ans<<endl;
}
}
printf("%lld\n",ans);
return 0;
}
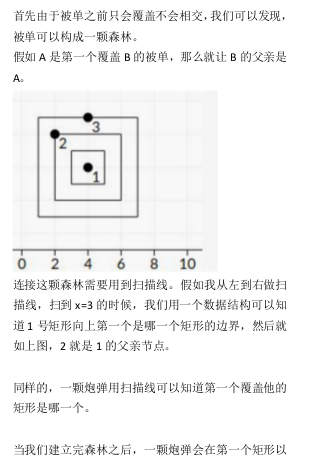
T2:床单
考场用最后的五分钟将33pts的代码改成了13pts,原因是:

我理解成:若打到了小床单上,小床单下的大床单即使没为射击点上也会被染色,大床单染色又会下传,然后我就建了个图,无了
正解没写

模拟测试46

考场发现T4欧拉定理可冲,发现模数转欧拉函数后还不是质数,没往CRT上想就走了
两个小时后发现自己T1还没调出来,看到左右做题速度飞快,果断上个坼锁开下一道题
最后一个小时冲T1 \(O(nlogn^2)\)
改完后在更

