暑期集训day22考试整理
T1:置换
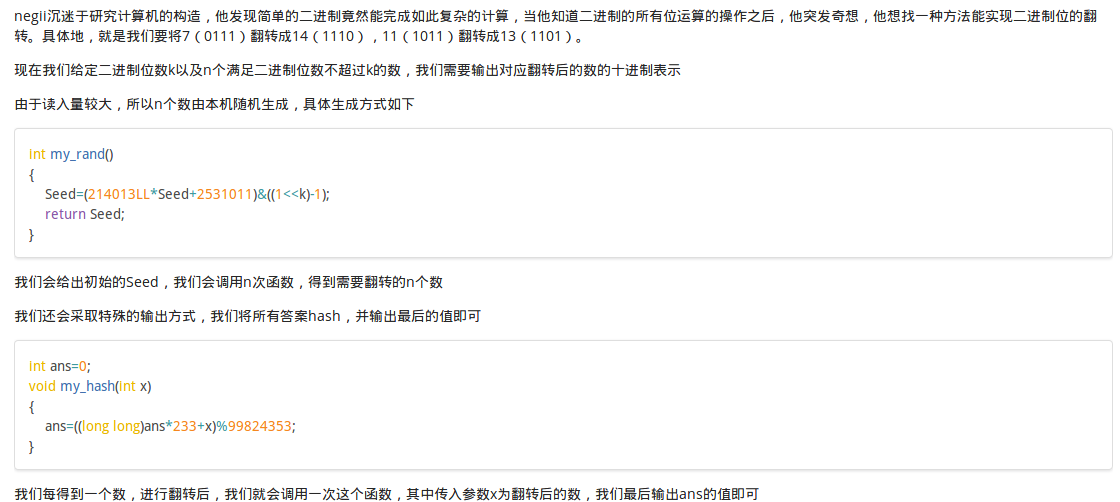
题目大意:
给一些数,让你求出这些数翻转后的总和
思路:
1.暴力翻转(\(90pts\))
暴力就完事了,不过当时以为时间复杂度没问题,就直接跳了,没想到被搞了\(30\)\(pts\)
对每一个数转成二进制,然后翻转。理想时间复杂度:\(O(2^k*25)\)
由于带了个\(25\)的数,所以直接\(T\)掉
代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1e6+5,INF=0x3f3f3f3f;
char buf[1 << 20], *p1 = buf, *p2 = buf;
char getc() {
if(p1 == p2) {
p1 = buf;
p2 = buf + fread(buf, 1, 1 << 20, stdin);
if(p1 == p2) return EOF;
}
return *p1++;
}
inline int read(){
int s=0,w=1;
char ch=getc();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getc();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getc();
return s*w;
}
const int p = 99824353;
int Seed,n,k,a[maxn],ans;
signed main(){
n = read(), k = read(), Seed = read();
int c[31]={},tot=0,sum=0;
int x;
for(register int i=1;i<=n;i++){
Seed=(214013LL*Seed+2531011)&((1<<k)-1);
memset(c, 0, sizeof c);
x = Seed;
tot=0,sum=0;
while(x){
c[tot]=x%2;x/=2;
tot++;
}
for(register int i=0;i<k;i++){
if(c[i]==1)sum+=1<<(k-i-1);
}
ans=((long long)ans*233%p+sum);
if(ans > 99824353) ans -= p;
}
printf("%d\n", ans);
return 0;
}
2.递推(\(100pts\))
由于数的上限是\(2^{25}\),所以可以直接把每一个二进制数翻转后的数给预处理出来,柿子:
(别问我为什么不写\(&\),latex打不出来这玩意)
表示这一二进制数可由前一位二进制数转移过来
举个例子:
\(10111\)翻转后是\(11101\)
\(10111\)要从\(01011\)转移过来
\(01011\)翻转后是\(11010\)
\(11010\)--->\(11101\) 的过程是\(a>>1|((i与1)<<(k-1))\)
时间效率:\(O(2^{25})\)
代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=(1<<25)+5,INF=0x3f3f3f3f,p = 99824353;
char buf[1<<20],*p1=buf,*p2=buf;
int Seed,n,k,a[maxn],ans;
char getc(){
if(p1==p2){
p1=buf;
p2=buf+fread(buf,1,1<<20,stdin);
if(p1==p2)return EOF;
}
return *p1++;
}
inline int read(){
int s=0,w=1;
char ch=getc();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getc();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getc();
return s*w;
}
int main(){
n=read(),k=read(),Seed=read();
int c[31]={},tot=0,sum=0;
for(int i=0;i<=(1<<k);i++){
a[i]=(a[i>>1]>>1)|((i&1)<<(k-1));
//cout<<a[i]<<endl;
}
for(register int i=1;i<=n;i++){
Seed=(214013LL*Seed+2531011)&((1<<k)-1);
// cout<<Seed<<" "<<a[Seed]<<endl;
ans=((long long)ans*233+a[Seed])%p;
}
printf("%d\n", ans);
return 0;
}
T2:字符串

题目大意:
对于后一半的字符串,咨询是否有回文中心且回文串的一半是回文中心到字符串尾,对于前一半的字符串,不断跳跃到回文串的结尾,看最后结尾是否是字符串尾
考场爆零了,唉
关键:

加了特判:
特判一删:
我真天才昨天就为了多拿点部分分,加几个特判,\(40pts\)-->\(20pts\),今天又在这跌倒了
1.暴力(\(60pts\))
暴力,暴力就完事了
如果是字符串后一半,直接检查是否存在回文串到字符串尾;如果是前一半,就不断跳跃,每一次跳到回文串尾,看是否能到达字符串尾
最差效率:\(O(n^2)\) (但是常数极其小,可能是\(n\sqrt n\)的)
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1e6+5,INF=0x3f3f3f3f;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s*w;
}
int n,path[maxn];
char a[maxn];
bool check(int now){
int l=now-1,r=now+1;
while(r<=n){
if(a[l]!=a[r])return 0;
l--;r++;
if(l==0)now=r-1,l=now-1;
}
return 1;
}
int main(){
int T=read();
while(T--){
memset(path,0,sizeof(path));
int tot=0;
scanf(" %s ",a+1);
n=strlen(a+1);
for(int i=n;i>(n+1)/2;i--){
int flag=0;
for(int d=2,l,r;d<=n-i+1,(l=i-d+1)>=1,(r=i+d-1)<=n;d++){
if(a[l]!=a[r]){flag=1;break;}
}
if(flag==0)path[++tot]=i;
}
for(int i=(n+1)/2;i>=1;i--){
if(check(i))path[++tot]=i;
}
for(int i=tot;i>=1;i--){if(path[i]!=path[i+1])printf("%d ",path[i]);}
puts(" ");
}
return 0;
}
2.Manacher(\(100pts\))
有这么方便的回文串算法,为何不用呢
同样,对于后一半,直接检查当前回文中心的回文串是否能扩展到串尾,反之就跳跃
时间效率:\(O(n)\)
然而,
拒绝冷门(阴间)算法,从我做起
3.哈希(\(100pts\))
啊哈,正常的字符串题都能用哈希,这题检查是否是回文串,直接正着搞一遍哈希,倒着搞一遍哈希,最后判断就行了。记得注意倒着的哈希与正着的哈希搞字符串的时候也是倒着的
代码:
/*
3
aabbab
ababab
aaaaaaaaaaaaaa
*/
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ull unsigned long long
using namespace std;
const int maxn=1e6+5,INF=0x3f3f3f3f,base=233;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s*w;
}
ull h[maxn],g[maxn],poww[maxn],powx[maxn];
int n,path[maxn];
char a[maxn];
bool check(int now){
if(now==1)return 0;
if(now>(n+1)/2)return g[now]==h[now]-h[2*now-n-1]*poww[n-now+1];
else if(h[now]==g[now]-g[now*2]*poww[now])return check(now*2-1);
return 0;
}
int main(){
int T=read();
while(T--){
memset(h,0,sizeof(h));
memset(g,0,sizeof(g));
scanf(" %s ",a+1);
n=strlen(a+1);
if(n==1){puts("1");continue;}
poww[0]=powx[n+1]=1;
for(int i=1;i<=n;i++){
h[i]=h[i-1]*base+a[i];
poww[i]=poww[i-1]*base;
}
for(int i=n;i>=1;i--){
g[i]=g[i+1]*base+a[i];
powx[i]=powx[i+1]*base;
}
for(int i=1;i<=n;i++){
if(check(i))printf("%d ",i);
}
puts(" ");
}
return 0;
}
T3:饼干

题目大意:有\(n\)个饼干,一共\(3\)种,质量分别为\(a\) \(b\) \(a+b\),每块饼干可以放进\(n\)个盒子里,让你求出所有和为\(k\)的排列情况
1.暴力(\(50pts\))
一共三种饼干,枚举就完事了。
用简单的组合数学知识写出暴力的柿子
柿子:
代码:
/*
4 1 2 5
*/
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define int long long
using namespace std;
const int maxn=1e5+5,INF=0x3f3f3f3f,mol=998244353;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s*w;
}
int n,a,b,k,c[maxn],f[maxn],g[maxn],ans;
int qpow(int a,int x){
int now=1;
while(x){
if(x&1)now=now*a%mol;
a=a*a%mol;
x>>=1;
}
return now;
}
void Init(){
c[0]=1;
for(int i=1;i<=n+5;i++)c[i]=c[i-1]*i%mol;
}
inline int CC(int nn,int mm){
if(mm==0)return 1;
return c[nn]*qpow(c[mm],mol-2)%mol*qpow(c[nn-mm],mol-2)%mol;
}
signed main(){
n=read();a=read();b=read();k=read();
Init();
int cnt,sum;
for(register int i=0;i<=n&&i*a<=k;i++){
for(register int j=0;(j+i)<=n&&(j*b+i*a)<=k;j++){
for(register int p=0;(p+i+j)<=n&&((a+b)*p+i*a+j*b)<=k;p++){
if(i*a+j*b+p*(a+b)==k){
sum=CC(n,i+j+p)*c[i+j+p]%mol*qpow(c[i],mol-2)%mol*qpow(c[j],mol-2)%mol*qpow(c[p],mol-2)%mol;
ans=(ans+sum)%mol;
}
}
}
}
cout<<ans;
return 0;
}
2.推柿子2代(\(100pts\))
由于第三个饼干重量是\(a+b\),所以可以直接从1到n枚举前两块饼干,前两块饼干的重合部分,就是第三块饼干
柿子:
(\((k-i*a)%b==0\),即剩下的重量必须整好放下第二块饼干)
但是,这破题细节特别多,很难想象考试时竟然有人A了(gyzNB)
细节1:\(min(a,b)==0\)并且\(k!=0\)
柿子:$$C_n^{k/max(a,b)}\times 2^k$$
把\(k/max(a,b)\)个饼干放进\(n\)个盒子,方案数为\(C_n^{k/max(a,b)}\)
由于其中一个饼干质量为\(0\),所以对所有的盒子,都有放与不放质量为\(0\)的饼干的两种选择
细节2:不写了,看代码,不会就用暴力辅助程序盯出来
代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define int long long
using namespace std;
const int maxn=1e7+5,INF=0x3f3f3f3f,mol=998244353;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
return s*w;
}
int n,a,b,k,c[maxn],f[maxn],g[maxn],ans;
int qpow(int a,int x){
int now=1;
while(x){
if(x&1)now=now*a%mol;
a=a*a%mol;
x>>=1;
}
return now;
}
void Init(){
c[0]=1;
for(int i=1;i<maxn;i++)c[i]=c[i-1]*i%mol;
}
inline int CC(int nn,int mm){
if(mm==0)return 1;
if(mm>nn)return 0;
return c[nn]*qpow(c[mm],mol-2)%mol*qpow(c[nn-mm],mol-2)%mol;
}
signed main(){
n=read();a=read();b=read();k=read();
Init();
if(a==0&&b==0&&k==0)return cout<<qpow(2,n*2),0;
if(a!=0&&b!=0&&k==0)return puts("1"),0;
if(k==0)return cout<<qpow(2,n),0;
if(a==0&&b==0)return puts("0"),0;
if(a==0)swap(a,b);
if(b==0&&k==0){
if(k%a!=0)return puts("0"),0;
return cout<<CC(n,k/a),0;
}
if(b==0&&k!=0)return cout<<CC(n,k/a)*qpow(2,n)%mol,0;
for(register int i=0;i<=n&&i*a<=k;i++){
if((k-i*a)%b==0&&(k-a*i)/b<=n)ans=(ans+CC(n,(k-a*i)/b)*CC(n,i)%mol)%mol;
}
cout<<ans;
return 0;
}
T4:空间宝石
爬,懒,不会,咕咕咕

