#洛谷 P3842 [TJOI2007]线段

P3842 [TJOI2007]线段

---

思路

1.出发点

显然显然显然（重要的事情说三遍），这一行的终点可能是线段的左边也可能是线段的右边，所以要想走完这一行的线段，就需要从上一行的左端点或右端点，进而就有了下面的讨论

2.讨论

计f[0][i]为走完第i行的线段且

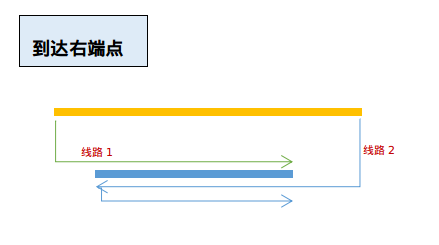
情况1：上一行线段在左，下一行线段在右

此时分两种图：

很显然，这两种可能可以合并

第一种图：

图1：

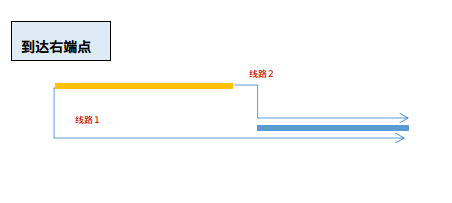
这里指出一个误区：明明线路\(2\)比线路\(1\)要优秀，为什么还要考虑呢？其实很简单，\(f[0][i-1]\)可能要比\(f[1][i-1]\)小很多，而不是\(f[1][i-1]\)一定大于\(f[0][i-1]\)，所以\(f[0][i-1]+abs(r[i]-l[i-1])\)（从上一行左端点到这一行右端点）可能小于\(f[1][i-1]+abs(r[i-1]-r[i])\)（从上一行右端点到这一行右端点）

图2：

状态转移方程为：

  f[0][i]=min(f[0][i-1]+abs(r[i]-l[i-1]),f[1][i-1]+abs(r[i-1]-r[i]))+len[i]+1;
  f[1][i]=min(f[0][i-1]+abs(l[i-1]-l[i]),f[1][i-1]+abs(r[i-1]-l[i]))+len[i]+1;

第二种图：

图1：

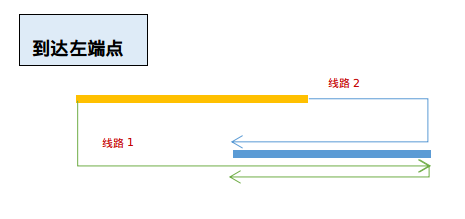
图2：

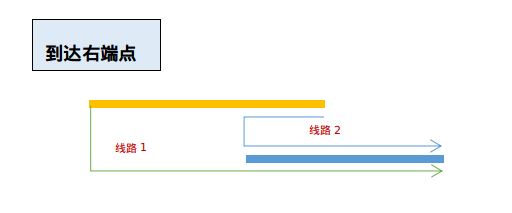
状态转移方程为：

  f[0][i]=min(f[0][i-1]+abs(r[i]-l[i-1]),f[1][i-1]+abs(r[i-1]-r[i]))+len[i]+1;
  f[1][i]=min(f[0][i-1]+abs(l[i-1]-l[i]),f[1][i-1]+abs(r[i-1]-l[i]))+len[i]+1;

惊奇的发现，状态转移方程竟然一样，这样就减少判断缩减了代码

情况2：上一行线段在中，下一行线段在中

此时也分两种图：

显然这两种也可以合并

同样四张图：

状态转移方程：

  f[0][i]=min(f[0][i-1]+abs(r[i]-l[i-1]),f[1][i-1]+abs(r[i-1]-r[i]))+len[i]+1;
  f[1][i]=min(f[0][i-1]+abs(l[i-1]-l[i]),f[1][i-1]+abs(r[i-1]-l[i]))+len[i]+1;

我们又要口矣了，两种大情况的状态转移方程也一样诶，显然第三种情况（上一行线段在右，下一行线段在左）也是这个状态转移方程，都可以合并就不用判断了诶诶诶（当然可以自己在画画第三种情况的图）

代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=2e4+5,INF=0x3f3f3f3f,mol=1000007;
int n,m,f[2][maxn],a[maxn],l[maxn],r[maxn],len[maxn];
inline int read(){
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')s=s*10+ch-'0',ch=getchar();
	return s*w;
}
int main(){
	//freopen("a.in","r",stdin);
	n=read();
	for(int i=1;i<=n;i++)l[i]=read(),r[i]=read(),len[i]=r[i]-l[i];
	f[0][1]=r[1]-1+len[1];f[1][1]=r[1]-1;
	for(int i=2;i<=n;i++){
		f[0][i]=min(f[0][i-1]+abs(r[i]-l[i-1]),f[1][i-1]+abs(r[i-1]-r[i]))+len[i]+1;
		f[1][i]=min(f[0][i-1]+abs(l[i-1]-l[i]),f[1][i-1]+abs(r[i-1]-l[i]))+len[i]+1;
	}
	cout<<min(f[0][n]+n-l[n],f[1][n]+n-r[n]);
	
}

OVER～