【线型DP】【LCS】UVA_10635 Prince and Princess

嘤嘤嘤，我又来了，刚A完就写，这个沙雕题有丶恶心、                  ？？？时间4.11发现所有表情包都莫得了

---

 

题目：

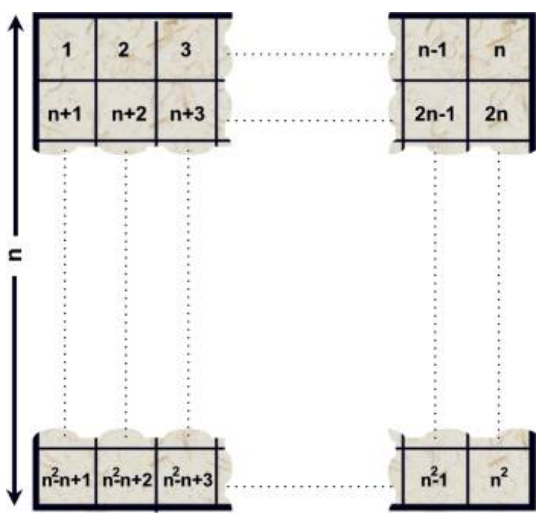
In an n×n chessboard, Prince and Princess plays a game. The squares in the chessboard are numbered 1, 2, 3, . . . , n∗n, as shown below:

 

Prince stands in square 1, make p jumps and finally reach square n ∗ n. He enters a square at most once. So if we use xp to denote the p-th square he enters, then x1, x2, . . . , xp+1 are all different. Note that x1 = 1 and xp+1 = n ∗ n. Princess does the similar thing – stands in square 1, make q jumps and finally reach square n ∗ n. We use y1, y2, . . . , yq+1 to denote the sequence, and all q + 1 numbers are different. Figure 2 belows show a 3×3 square, a possible route for Prince and a different route for Princess.

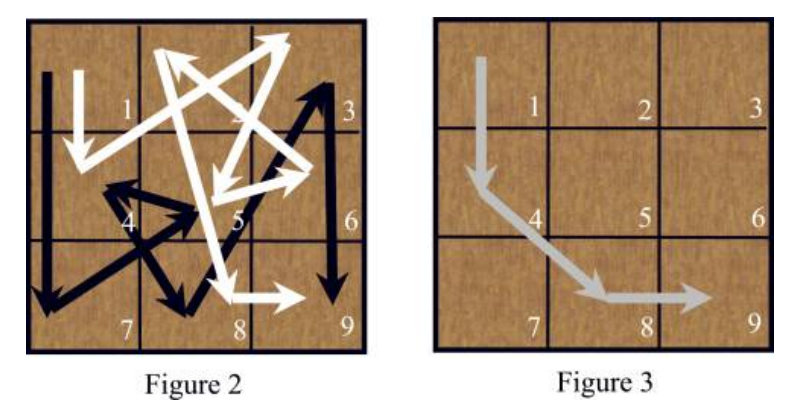
The Prince moves along the sequence: 1 –> 7 –> 5 –> 4 –> 8 –> 3 –> 9 (Black arrows), while the Princess moves along this sequence: 1 –> 4 –> 3 –> 5 > 6 –> 2 –> 8 –> 9 (White arrow). The King – their father, has just come. “Why move separately? You are brother and sister!” said the King, “Ignore some jumps and make sure that you’re always together.” For example, if the Prince ignores his 2nd, 3rd, 6th jump, he’ll follow the route: 1 –> 4 –> 8 –> 9. If the Princess ignores her 3rd, 4th, 5th, 6th jump, she’ll follow the same route: 1 –> 4 –> 8 –> 9, (The common route is shown in figure 3) thus satisfies the King, shown above. The King wants to know the longest route they can move together, could you tell him? 

n×n的棋盘中，王子和公主玩游戏。棋盘上的方块编号

1 2 3 。 。 ，n ∗ n，如下所示：

王子站在方格1中，使p跳跃，最后达到方格n ∗ n。他最多只能进入一个广场

一旦。因此，如果我们使用xp表示他输入的第p个平方，则x1，x2，。 。 。 ，xp + 1都不同。注意

x1 = 1且xp + 1 = n * n公主做类似的事情–站在广场1，使q跳，最终达到平方n ∗ n。我们使用y1，y2，。 。 。 ，yq + 1表示序列，并且所有q +1个数字均为不同。下面的图2显示了一个3×3的正方形，这是Prince的可能路线，而Princess的路线则不同。王子按照以下顺序移动：1 –> 7 –> 5 –> 4 –> 8 –> 3 –> 9（黑色箭头），而公主按照以下顺序移动：1 –> 4 –> 3 –> 5> 6 –> 2 –> 8 –> 9（白色箭头）。国王–他们的父亲，刚来。 “为什么要分开移动？你是兄弟姐妹！”国王说，“应该忽略一些跳跃，并确保您一直在一起。”例如，如果王子忽略了他的第二，第三，第六跳，他将遵循以下路线：1 –> 4 –> 8 –>9.如果公主不理her她的第三，第四，第五，第六跳，她将遵循相同的路线：1 –> 4 –> 8 –>9因此，如图9所示，通用路线如图3所示。国王想你知道他们可以一起走的最长路线，你能告诉他吗？

输入值

输入的第一行包含一个整数t（1≤t≤10），其后是测试用例的数量。对于每种情况，第一行包含三个整数n，p，q（2≤n≤250，1≤p，q <n * n）。第二行包含[1]范围内的p + 1个不同的整数。 。 。 n * n]，王子的序列。第三行在[1。范围内包含q + 1个不同的整数。 。 。 n * n]，公主的顺序。

输出量

对于每个测试案例，请输出案例编号和最长路径的长度。

样本输入

1

3 6 7

1 7 5 4 8 3 9

1 4 3 5 6 2 8 9

 

样本输出

Case 1: 4

---

框架：

拿到这题第一反应——花里胡哨，前面王子公主一顿操作猛如虎，最后竟然就让我们求个最大公共上升子序列，抱着这样的想法，我带着老师上课写的优化过的O(n*n)LCIS模板以及仰天大笑的姿态提交了这道题，直接上代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;//数组别小了 
const int maxn=250*250+5,INF=0x3f3f3f3f;
int n,m,t,p,q,f[2][maxn],a[maxn],b[maxn];
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}//朴素的快读 
int main(){
    freopen("a.in","r",stdin);
    t=read();
    int cnt=0;
    while(++cnt<=t){
        n=read();
        p=read();
        q=read();
        int maxmax=0;//听说register能省点时间
        for(register int i=1;i<=n*n;i++){ 
            f[0][i]=f[1][i]=a[i]=b[i]=0;
        }
        for(register int i=1;i<=p+1;i++)a[i]=read();
        for(register int i=1;i<=q+1;i++)b[i]=read();
        for(register int i=1;i<=p+1;i++){ 
            int ans=0;//lcis模板
            for(register int j=1;j<=q+1;j++){
                f[i%2][j]=f[(i-1)%2][j];//喜欢这样做滚动数组 
                if(a[i]>b[j]&&ans<f[i%2][j])ans=f[i%2][j];
                if(a[i]==b[j])f[i%2][j]=ans+1;
                maxmax=max(maxmax,f[i%2][j]);
            }//解释：因为lcis一定是从左或从上转移过来 
             //所以能用滚动数组节省时间空间 
        }
        printf("Case %d: %d\n",cnt,maxmax);
    }
}

然后结局很惨：

在这几个小时的时间里，我以为是某些地方时间超了那么一丢丢，于是从memset改到循环初始化，从cin改到快读，最后再压了压数组大小，喜提11连错

然后我才发现我被样例所蛊惑，这道题求得不是lcis，是lcs（很蠢），但lcs和lcis都是n*n的时间，所以也不用看了，但为了矫正，还是上一下代码（是不是相当于给大家复习了一下lcs和lcis）：

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;//数组别小了 
const int maxn=250*250+5,INF=0x3f3f3f3f;
int n,m,t,p,q,f[2][maxn],a[maxn],b[maxn],ans;
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}//朴素的快读 
int main(){
    freopen("a.in","r",stdin);
    t=read();
    int cnt=0;
    while(++cnt<=t){
        n=read();
        p=read();
        q=read();
        int maxmax=0，k=0;//听说register能省点时间
        for(register int i=1;i<=n*n;i++){ 
            k=!k;
            f[k][i]=f[!k][i]=a[i]=b[i]=0;
        }
        for(register int i=1;i<=p+1;i++)a[i]=read();
        for(register int i=1;i<=q+1;i++)b[i]=read();
        for(int i=1;i<=p+1;i++){
            k=!k;//另一种滚动数组,用^k也行
            for(int j=1;j<=q+1;j++){
                if(a[i]==b[j])f[k][j]=f[!k][j-1]+1;//字符相同就从左上角转移 
                else f[k][j]=max(f[!k][j],f[k][j-1]);//不相同就从上或左中的最大的转移 
                ans=max(ans,f[k][j]);
            }
        }
        printf("Case %d: %d\n",cnt,ans);
    }
}

 

 

 

---

 时间4.9，开肝

 

---

 

后来我迫不得已查了下题解，发现这道题并不是用n*n效率的lcis模板，而是用nlogn的简化版先上代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<map>//map的库，当然可以不用map直接用数组对应 
using namespace std;
const int maxn=250*250+5,maxe=250*250+5,INF=0x3f3f3f3f;
int n,m,t,p,q,f[maxe],a[maxn],b[maxn],low[maxn];
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}//朴素快读 
int main(){
    freopen("a.in","r",stdin);
    t=read();
    int cnt=0;
    while(++cnt<=t){
        n=read();
        p=read();
        q=read();
        int maxmax=0;
        memset(low,0,sizeof(low));
        map<int,int> mp;
        for(register int i=1;i<=p+1;i++)a[i]=read(),mp[a[i]]=i;
        int len=0;//这里对第一组序列进行对应
        for(register int i=1;i<=q+1;i++){
            b[++len]=read();//如果第二组序列中出现了前一组序列的数的位置就加到数组里 
            if(mp.find(b[len])==mp.end())len--;//没有就删除 
            else b[len]=mp[b[len]];
        }
        //for(int i=1;i<=len;i++)cout<<b[i]<<" ";
        int len1=1;
        low[1]=b[1];
        for(register int i=2;i<=len;i++){
            if(low[len1]<b[i])low[++len1]=b[i];
            else low[lower_bound(low+1,low+len1+1,b[i])-low]=b[i];
        }//找一下新序列中最长上升子序列就是结果，想成友好城市保证顺序一致也行 
        
        printf("Case %d: %d\n",cnt,len1);
    }
}

解释：

1.我们现行比较两个序列，因为要想求最长相等子序列，最后的子序列中肯定包含两个序列中的相等的字符，所以我们先取重，同时对第一组序列每一个字符进行编号，在输入第二组序列时一边去重一边把重复字符的对应填在新数组中，最后对新数组进行LIS，保证两个子序列的顺序相同

2.那LCS能用nlogn的时间写，那么我们还学原来那个n*n的干什么？在这里我们要注意，本体有一个条件：一个序列中每一个数都不同（题目里标红了），这样我们才可以用对应，而对两个相同的数我们就不能保证有两个不同的对应，所以只能用n*n的LCS。什么，你不知道两个相同的数我们不能保证有两个不同的对应？回去做潜伏者。什么,你说要用unique去重？那你错了没人救你。

总结：

这道题主要用了map中的对应，所以建议还是回去做做潜伏者巩固巩固

今晚写打鼹鼠的题解，争取写出线型动归和区间动归的模板，明天写多边形的题解

——2020/4/8~2020/4/9