【数量关系】第二十三节：最优化问题

　　

 

例题

1、某电商平台每隔5千米有一座仓库，共有A、B、C、D四座仓库，图中数字表示各仓库库存货物的吨数。现需要把所有的货物集中存放在其中某一个仓库中，如果每吨货物运输1千米需要运费3元，要使运费最少，则需将货物集中到哪座仓库？

　　　　A.仓库A　　B.仓库B　　C.仓库C　　D.仓库D

思路：

　　每一步路径切开进行分析，10,|20,15,25，左侧轻，A搬到B点。

　　30|15,25，依旧左侧轻，B搬到C点，45|25，此时左侧重，右侧搬到C点。

　　树形图同此分析方法。

 

2、某工厂生产甲和乙两种产品，已知生产1件甲产品可获利1000元，消耗A和B材料分别为2千克、3千克；生产1件乙产品可获利1700元，消耗A和B材料分别为5千克、4千克。若有A和B材料分别为200千克、240千克，则生产甲、乙两种产品能取得的最大利润是：

　　　　A.85200元　　B.86278元　　C.85900元　　D.86600元

思路：

　　要从剩下的材料尽量少的角度去讨论，不能只从哪个贵就只生产那个！

　　第二步：转换成周期问题。

　　此时B材料比A材料多40克，而且甲产品的b消耗量比a多1kg，所以先提前生产40个甲材料，形成AB材料相等状态。

　　∴40个甲产品 = 40*2 = 80kg A材料，40*3=120kg B材料

　　∴此时剩余A：120kg，B：120kg。120÷7=17...1，7是甲乙产品都是消耗7个材料AB。

　　∴40*1000+17*(1000+1700)　　尾数法。

 

3、某社区道路如下图所示，社区民警早上9点整从A处的办公室出发，以每分钟50米的速度对社区内每一条道路进行巡查(要求完整走过整个社区内的每一段道路)，问他最早什么时候能完成任务返回办公室?

 

　　　　A.9∶54　　B.9∶50　　C.9∶47　　D.10∶00

思路：

　　一笔画问题，需要满足两个条件之一。

　　①所有点全都是偶点，

　　②有且仅有两个奇点，必须从其中一个奇点出发另一个奇点结束。

　　此图需要将奇点转换成偶点。重复走一次即可。

　　

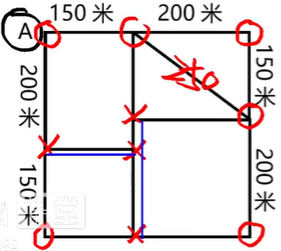
　　　　350×7+250=2700,2700÷50=54

 

4、A、B两地分别有10台和6台型号相同的机器，准备配送到E、F两地，其中E地11台，F地5台，若每台机器从A到E和F的物流费用分别为350元和550元，从B到E和F的物流费用分别为600元和900元，则配送这16台机器的总物流费用最少为：

　　　　A.7850元　　B.8100元　　C.8400元　　D.8700元

思路：

　　谁省的钱尽量多，就往那里运。

　　

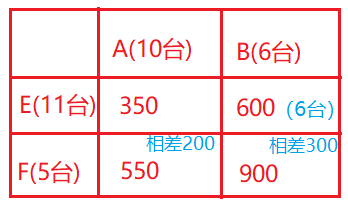
 　　B运往E省300块，所以B的全部运往E点，剩下的由A补足。

　　5*350+5*550+6*600=8100