【数量关系】第十七节:概率问题
概率问题的两类题型
①基本概率问题:
所有的结果 ÷ 所有的可能 (例如:抛骰子1/6)
②思想概率问题
由条件中多个已知概率问题求得未知概率的问题(只要在条件中出现具体概率)
①同时发生:相乘
②并列发生:相加
例题
S01:某公司将在本周一至周日连续七天举办联谊会,某员工随机地选择其中的连续两天参加联谊会,那么他在周五至周日期间连续两天参加联谊会的概率为
A、1∶2 B、1∶3 C、1∶4 D、1∶6
思路:
基本概率问题。一共有6种可能,2种结果得:2/6
S02:甲乙两人相约骑共享单车运动健身。停车点现有9辆单车,分属3个品牌,各有2、3、4辆。假如两人选择每一辆单车的概率相同,两人选到同一品牌单车的概率约为:

思路:
求概率时,分子分母要同时有序或者同时无序。
所有可能C(2,9),所有结果:C(2,2)+C(2,3)+C(2,4)
方法二:选A车时是2/9,再选A车是1/8+选B车时是3/9,再选B车是2/8+选C车时是4/9,再选X车是3/8
L01:某市举行“新春杯”足球比赛,对16支参赛队伍进行小组赛分组抽签。抽签箱中分别装有红、黄、绿、蓝的小球各四个,抽到相同颜色小球的队伍进入同一小组。则第一支抽签队伍与第二支抽签队伍被分在同一小组的概率为( )。
A. B.
B. C.
C. D.
D.
思路:
谁和谁处在同一个小组称为:两人同组问题。
第一支队伍抽签没有概率。此时第二支队伍抽签还有15种可能,如果要和第一组同色则只有3种结果,得1/5
核心思想:一静一动。只需要看另外一个人。
方法二(排列组合):所有可能C(2,16),同一组选2个 C(2,4)×4,×4是因为有4组球同样情况。
G02:某市公安局从辖区2个派出所分别抽调2名警察,将他们随机安排到3个专案组工作,则来自同一派出所的警察不在同一组的概率是:
A. B.
B. C.
C. D.
D.
思路:
假设警察a1a2,b1b2,3个空位。先分派a1a2b1,那么b2一共有3种可能,有2种结果不在同一派出所。
L02:某会议室共5排座位,每排座位数依次为10、9、8、7、6个,甲、乙两人随机选择座位入座,则他们左右相邻的概率:
A.不到2% B.在2%到5%之间 C.在5%到10%之间 D.高于10%
思路:
一共C(2,40)种可能。如果是6个坐,就5种结果,7个坐就6种....共35种结果。
此题不适用两人同组问题
L03:某基层机关有甲和乙两个办公室,共有10名员工。其中甲办公室人数为乙办公室人数的1.5倍,现从这10名员工中随机抽出2人借调到上级机关,问借调的人来自同一办公室的概率为:
A.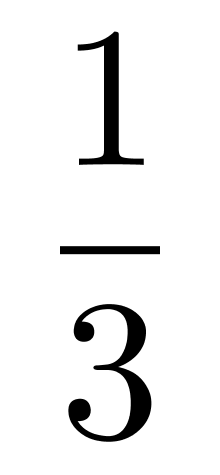 B.
B.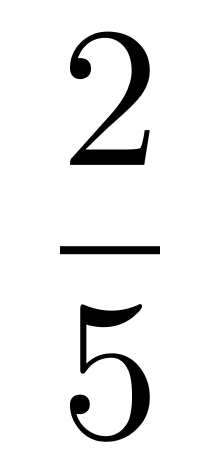 C.
C.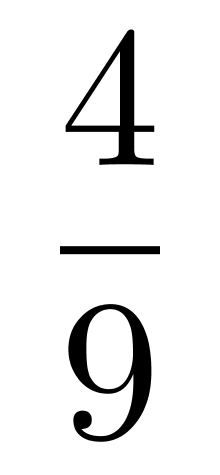 D.
D.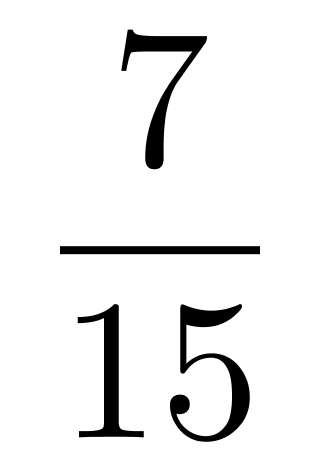
思路:
所有可能为:C(2,10),来自甲办公室结果为C(2,6),+乙办公室结果为C(2,4)
L04:某驾校甲、乙、丙三位学员在科目二考试中能通过的概率分别为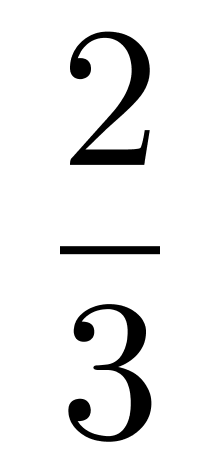 、
、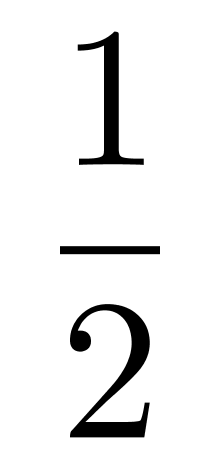 、
、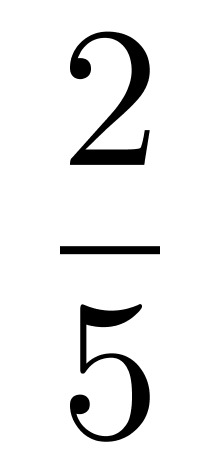 ,那么,这三位学员中恰好有两位学员通过科目二考试的概率为:
,那么,这三位学员中恰好有两位学员通过科目二考试的概率为:
A.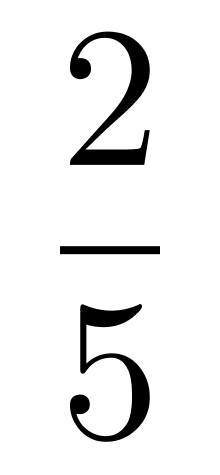 B.
B.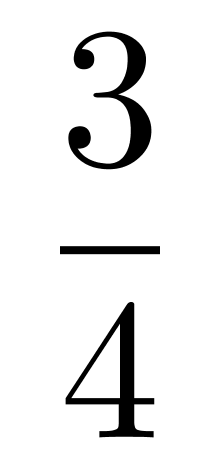 C.
C.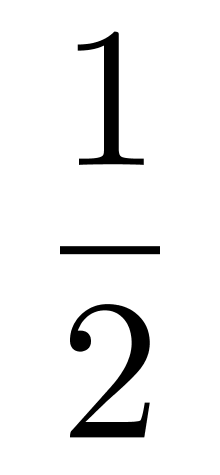 D.
D.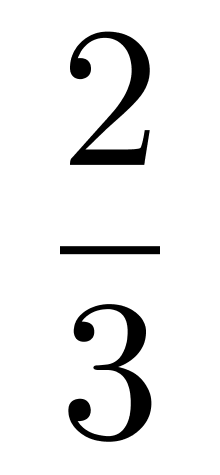
思路:
计算甲乙通过,丙没通过;2/3*1/2*3/5 = 6/30,再计算乙丙通过,丙甲通过的概率相加即可。
L05:小李和小张参加七局四胜的飞镖比赛,两人水平相当,每局赢的概率都是50%。如果小李已经赢2局,小张已经赢1局,最终小李获胜的概率是?
思路:
分类讨论:如果在第5局胜出,则4,5局都要赢概率为1/2×1/2;
如果在第6局胜出,则4,5局选1局赢,剩下得输,第6局赢,得C(1,2)×1/2×1/2 ×1/2
如果在第7局胜出,则4,5,6局选1局赢,剩下得输,第7局赢,得C(1,3)×1/2×1/2×1/2 ×1/2
L06:某仓库存放三个厂家生产的同一品牌洗衣液,其中甲厂生产的占20%,乙厂生产的占30%,剩余为丙厂生产的,且三个厂家的次品率分别为1%,2%,1%,则从仓库中随机取出一件是次品的概率为:
A.1% B.2% C.1.6% D.1.3%
思路:
抽到甲且次品概率为:20%*1%,....,最后相加。
G01:苹果有每盒3个、5个和8个三种不同的包装。如果随机拿4盒,苹果总个数多于20个且为偶数的概率:
A . 低于25% B . 在25%~30%之间 C . 在30%~35%之间 D . 高于35%
思路:
不考虑概率,随机取4盒一共有3^4共81种拿法,其中3553和3355是不同的拿法。
4盒且是偶数拿法有8888:1种,8855:C(2,4)种【先选2个位置放8C(2,4),剩下就只能放5】,8833:C(2,4)种、8835:C(2,4)×A(2,2)种
母题研究
1、某单位有3项业务要招标,共有5家公司前来投标,且每家公司都对3项业务发出了投标申请,最终发现每项业务都有且只有1家公司中标。如5家公司在各项业务中中标的概率均相等,问这3项业务由同一家公司中标的概率为( )。
A.1/25 B.1/81 C. 1/125 D. 1/243
思路:
总的可能为5*5*5=125,中标结果为同一家的可能有5种。
2、A、B两地间有三种类型列车运行,其中高速铁路动车组列车每天6车次,普通动车组列车每天5车次,快速旅客列车每天4车次。甲、乙两人要同一天从A地出发前往B地。假设他们买票前没有互通信息,而且火车票票源充足,问他们买到同一趟列车车票的概率有多大?
A . 小于10% B . 10%到20%之间 C . 20%到25%之间 D . 25%到30%之间
思路:
两人同组问题:一静是甲先买了一趟,乙一共有15种可能,那么买到同一趟是1/15
方法二:排列组合,要么同时买到第一趟要么第二趟,...一共15种结果。
甲有15种坐车可能×乙15种一共225种可能。
3、抽奖箱子里剩下8张奖券,其中5张有奖,3张无奖,小王有两次抽奖机会,他不放回地依次抽取两张奖券,则这两张奖券中一张有奖一张无奖的概率是:
思路:
分类讨论:第一张有奖第二张没奖:5/8×3/7 = 15/56
第一张没奖第二张有奖:3/8×5/7 = 15/56
4、一张纸上画了5排共30个格子,每排格子数相同。小王将1个红色和1个绿色棋子随机放入任意一个格子(2个棋子不在同一格子),则2个棋子在同一排的概率:
A.不高于15% B.高于15%但低于20% C.正好为20% D.高于20%
思路:
两人同组问题,先确定一个棋子位置。另外一个棋子一共有29种放法,有5种在同一排。
5、某学校举行迎新篝火晚会,100名新生随机围坐在篝火四周,其中,小张与小李是同桌,他俩坐在一起的概率为:
思路:
两人同组问题,2/99
6、箱子中有编号为1~10的10个小球,每次从中抽出1个记下编号后放回,如果重复3次,则3次记下的小球编号乘积是5的倍数的概率是多少:
A . 43.2% B . 48.8% C . 51.2% D . 56.8%
思路:
5的倍数就是抽到5或者抽到10,反向讨论不是5的倍数,即抽不到5和10的概率为0.8,抽3次一共0.8^3=0.512
7、在小李等车期间,有豪华型、舒适型、标准型三辆旅游车随机开过。小李不知道豪华型的标准,只能通过前后两辆车进行对比。为此,小李采取的策略是不乘坐第一辆,如果发现第二辆比第一辆车更豪华就乘坐;如果不是,就乘坐最后一辆。那么,他能乘坐豪华型旅游车的概率是
设豪华型、舒适型、标准型为C、B、A。一共有A(3,3)=6种排序可能。
符合的排列为ACB、BCA、BAC3种。所以1/2
8、某次知识竞赛试卷包括3道每题10分的甲类题,2道每题20分的乙类题以及1道30分的丙类题。参赛者赵某随机选择其中的部分试题作答并全部答对,其最终得分为70分。问赵某未选择丙类题的概率为多少:
A . 1/3 B . 1/5 C . 1/7 D . 1/8
思路:
答对甲(3,10分),乙(2,20分),丙(1,30分)题目的数量选择有021,211,320
其中211包含了,从甲3种中选择2道,C(2,3),从乙2种中选择1道,C(1,2),共6种可能。加起来一共8种可能。
9、两支篮球队打一个系列赛,三场两胜制,第一场和第三场在甲队的主场,第二场在乙队的主场。已知甲队主场赢球概率为0.7,客场赢球概率为0.3。问甲队赢得这个系列赛的概率为多少?
A.0.512 B.0.768 C.0.7 D.0.812
思路:
三场两胜,分类讨论,1,2场赢:0.7*0.5,1,3场赢:0.7*0.5*0.7,2,3场赢:0.3*0.5*0.7
10、A、B、C三个厂家生产同一种乒乓球,不合格率分别为1%、2%和4%。现将三个厂家的产品按6∶3∶1的比例均匀混合后装入集装箱,从该箱中随机抽出1只乒乓球进行检测,若检测结果为不合格,则该只乒乓球是B厂生产的概率是:
A.0.3 B.0.375 C.0.4 D.0.425
思路:
假设一共有1000个球,则ABC分别有600,300,100,不合格有6,6,4。抽到B厂不合格有6/16
11、在一次产品质量抽查中,某批次产品被抽出10件样品进行检验,其中恰有两件不合格品,如果对这10件样品逐件进行检验,则这两件不合格品恰好在第五次被全部检出的概率是:
A.4/45 B.2/45 C.1/45 D.1/90
思路:
不合格品一共有C(2,10)=45种放法。第5次一定是不合格。所以第一个不合格品一定要在前4次检查出,有4种结果。


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律