【数量关系】第十节:行程问题
行程问题的四种类型
①S=V×T
②平均速度
平均速度公式: (等距离平均速度公式)
(等距离平均速度公式)
平均速度的理解:总路程÷总时间
看到等距离的问题,第一时间想到用平均速度公式求解。
③相对速度
相对速度公式:
加法:相遇问题,顺水问题,顺电梯问题
减法:追及问题,逆水问题,
在追及问题中,V相对,是单位时间内,甲比乙多跑的路程。S相对是甲比乙共多跑的路程。
在相遇问题中,V相对,是单位时间内,甲、乙共同跑的路程,S相对,是甲、乙共跑的路程。
④漂流问题(A->B:路程S,设V船,V水,T1(顺),T2(逆))
漂流问题公式:漂流时间(水由A到B走得时间):![]()
船在静水中的航行时间:![]()
![]()
例题
S01:小林在距家1.5公里的工厂上班。一天,小林出发10分钟后,父亲老林发现小林的手机没带,立即追出去,并在距离工厂500米的地方追上了他。如果老林追赶的速度比小林快6公里/小时,那么,下列关于小林速度x,求值所列方程正确的是:
1/x - 1/(x+6) = 1/6
思路:
单位统一,速度6km/h,时间差是1/6h,不能是10分钟。
S02:一个圆形的人工湖,直径为50公里,某游船从码头甲出发,匀速直线行驶30公里到码头乙停留36分钟,然后到与码头甲直线距离为50公里的码头丙,共用时2小时。问该游船从码头甲直线行驶到码头丙需用多少时间?( )
A、50分钟 B、1小时 C、1小时20分 D、1小时30分
补充:
任意以圆的直径为边的内截三角形都是直角三角形。
常考的三角形:勾三股四弦五(3,4,5)。或者5,12,13。
思路:
比例思维:70km:84分钟 = 50km:?分钟。(1.2倍关系)
L01:已知A、B两地相距600千米。甲、乙两车同时从A、B两地相向而行,3小时相遇。若甲的速度是乙的1.5倍,则甲的速度是:
A.60千米/小时 B.90千米/小时 C.100千米/小时 D.120千米/小时
思路:
普通列式子解方程。
15V*3+V*3=600,得V=80
L02:甲去北京出差,去时坐飞机,返回时坐高铁。若飞机的速度比高铁快3倍,且往返平均速度为480千米/小时,问甲乘坐的飞机速度为多少千米/小时?
A. 720千米/小时 B. 768千米/小时 C. 960千米/小时 D. 1200千米/小时
思路:
快3倍就是我是你的4倍,后续套公式
L03:从甲地到乙地111千米,其中有1/4是平路,1/2是上坡路,1/4是下坡路。假定一辆车在平路的速度是20千米/小时,上坡的速度是15千米/小时,下坡的速度是30千米/小时。则该车由甲地到乙地往返一趟的平均速度是多少? 单项选择题
A. 19千米/小时 B. 20千米/小时 C. 21千米/小时 D. 22千米/小时
思路:
平路的平均速度是20,上下坡的平均速度也是20。(设计好的题目)。与上下坡平路的路程占比无关。
L04:某宣讲团甲宣传员骑摩托车从红星村出发以20公里/小时的速度去相距60公里的八一村,1小时后由于路面湿滑,速度减少一半,在甲出发1小时后,乙宣传员以50公里/小时的速度开车从红星村出发追甲,当乙追上甲时,他们与八一村的距离为:
A.25公里 B.40公里 C.35公里 D.30公里
思路:
在追上的那一刻,乙需要比甲多跑20公里。S相对=20km。
L05:“梦想号”和“启航号”两列火车在两条平行轨道上匀速相向而行,“梦想号”的车长为270米,“启航号”的车长为360米。若“梦想号”的乘客从车窗看见“启航号”驶过的时间是8秒,则“启航号”的乘客从车窗看见“梦想号”驶过的时间是( )秒。
A.10 B.8 C.6 D.4
思路:
假设梦想号静止。
360米:8s = 270米:?s。(速度和相同,用比例思维)
L06:寒假第一天骑行社团从学校出发去滑雪,他们以20公里/小时的速度骑行2个小时到达滑雪场。游玩四小时后按原路以原速返回。骑行社团离开学校5.5小时后,辅导员派大客车以40公里/小时的速度沿相同路线迎接骑行社团。则大客车出发后与骑行社团相遇需要的时长是?()
A.30分钟 B.60分钟 C.50分钟 D.40分钟
L07:有A、B两家工厂分别建在河流的上游和下游,甲、乙两船分别从A、B港口出发前往两地中间的C港口。C港与A厂的距离比其与B厂的距离远10千米。乙船出发后经过4小时到达C港,甲船在乙船出发后1小时出发,正好与乙船同时到达。已知两船在静水中的速度都是32千米/小时,问河水流速是多少千米/时?
A.4 B.5 C.6 D.7
思路:
(32+V水)*3 - (32-V水)*4 = 10,得V水=6
L08:一艘游轮逆流而行,从A地到B地需6天;顺流而行,从B地到A地需4天。问若不考虑其他因素,一块塑料漂浮物从B地漂流到A地需要多少天?
A.12 B.16 C.18 D.24
G01:小张从甲地出发匀速前往乙地,同时小李和小王从乙地出发匀速前往甲地,小张和小李在途中的丙地相遇,小张和小王在途中的丁相遇,已知小张的速度比小李快一半,小王的速度比小李慢一半,则丙丁两地之间的距离与甲乙之间的距离之比为:
A. 2∶15 B. 1∶4 C. 3∶20 D. 1∶15
思路:
先设张,李,王,速度为3,2,1。相遇时速度比3:2,那么路程比也是3:2。相当于相遇时跑了全程的3/5。
3/4 - 3/5 = 3/20
T01: 甲和乙在长400米的环形跑道上匀速跑步,如两人同时从同一点出发相向而行,则第一次相遇的位置距离出发点有150米的路程;如两人同时从同一点出发同向而行,问跑得快的人第一次追上另一人时跑了多少米?
A.600 B.800 C.1000 D.1200
思路:
环形跑道,追及问题,追上时,快的人比慢的人多跑一圈。
速度比恒定不变,路程比也不变。
任意时间下 S甲:S乙=250:150,相差100米,追及时相差400米,所以=1000:600
T02:环形跑道的周长为400米,甲乙两人骑车同时从同一地点出发,匀速相向而行,16秒后甲乙相遇。相遇后,乙立即调头,6分40秒后甲第一次追上乙,问甲追上乙的地点距原来的起点多少米?
A.8 B.20 C.180 D.192
思路:
V甲+V乙=400÷16=25
V甲-V乙=400÷400=1
V甲=13,V乙=12。S甲=(13*16+13*400)÷400=13...208,400-208=192
T03:甲、乙两人同时从A、B两地相向而行,他们第一次相遇的地点距离B地12公里,此后两人继续前行,分别到达B、A两地后立即返回,在距离B地区4公里的地方再次相遇.请问A、B两地之间相距多远?
A.20千米 B.24千米 C.30千米 D.32千米
T04:两艘渡轮在同一时刻垂直驶离H河的甲、乙两岸相向而行,一艘从甲岸驶向乙岸,另一艘从乙岸开往甲岸,它们在距离较近的甲岸720米处相遇。到达预定地点后,每艘船都要停留10分钟,以便让乘客上船下船,然后返航。这两艘船在距离乙岸400米处又重新相遇。问:该河的宽度是多少?_____
补充:
①两次相遇中,单边行问题。
第一次相遇时,双方共走了1S。假设为1T时间,此时乙走到了S1。
第二次相遇时走了3S,∴一共走了3T时间,乙走了3S1。
第三次相遇时走了5S,....
公式:S = (3S1+S2)÷2
②两次相遇中,双边行问题。
第一次相遇时,双方共走了1S。假设为1T时间,此时甲走了S1。
第二次相遇时走了3S,∴一共走了3T时间,甲走了 S+S2=3S1,=》S=3S1-S2
第三次相遇时走了5S,....
公式:S = 3S1-S2
第n次相遇走了:(2n-1)S
T05:甲、乙两地相距210公里,a,b两辆汽车分别从甲、乙两地同时相向出发并连续往返于两地。从甲地出发的a汽车的速度为90公里/小时,从乙地出发的b汽车的速度为120公里/小时。问第2次从甲地出发后与b汽车相遇时,b汽车共行驶了多少公里?
A.560公里 B.600公里 C.620公里 D.650公里
思路:
一共走了3次,5S=5*210=1050,知道速度比求路程比,得b=600km
T06:丙地为甲、乙两地之间高速公路上的一个测速点,其与甲地之间的距离是与乙地之间距离的一半。A、B两车分别从甲地和乙地同时出发匀速相向而行,第一次迎面相遇的位置距离丙地500米。两车到达对方出发地后立刻原路返回,第二次两车相遇也为迎面相遇,问第二次相遇的位置一定
A.距离甲地1500米 B.距离乙地1500米 C.距离丙地1500米 D.距离乙、两中点1500米
思路:
第一次相遇时A车:1/3S+500
第二次相遇时A车:3(1/3S+500) = S+1500
母题研究
1、甲和乙在长400米的环形跑道上匀速跑步,如两人同时从同一点出发相向而行,则第一次相遇的位置距离出发点有150米的路程;如两人同时从同一点出发同向而行,问跑得快的人第一次追上另一人时跑了多少米( )
A.600 B.800 C.1000 D.1200
思路:
比例思维。S甲:S乙=250:150 (相差100米) = 1000:600 (相差400米时)
2、已知一形状为正六边形的跑道,边长为150米,甲、乙两人分别从两个相对的顶点同时出发,沿跑道相向匀速前进。两人第一次相遇时乙比甲多跑了50米,则甲、乙两人跑步的速度之比是:
A.3∶5 B.4∶5 C.5∶3 D.5∶4
思路:
路程比与速度比
3、小张和小王18:00分别从甲、乙两地同时出发,沿相同道路匀速相向而行。18:20小张到达丙地停留,18:40两人在丙地碰面并均以出发时速度继续行进。18:50小王到达甲地,问小张在几点到达乙地?
A.20:00 B.20:40 C.19:00 D.19:40

5、从A地到B地为上坡路。自行车选手从A地出发按A-B-A-B的路线行进,全程平均速度为从B地出发按B-A-B-A的路线行进的全程平均速度的。如自行车选手在上坡路与下坡路上分别以固定速度匀速骑行,问他上坡的速度是下坡速度的?
A.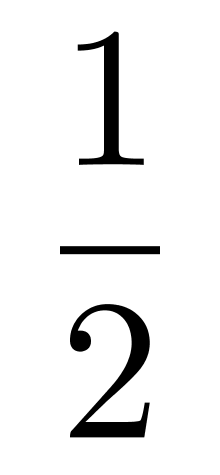 B.
B.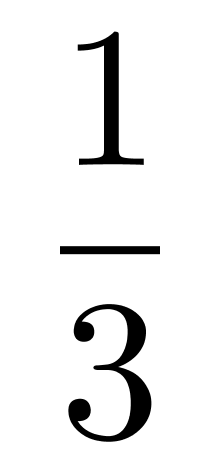 C.
C.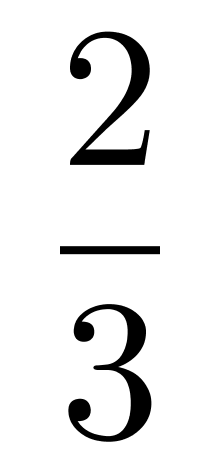 D.
D.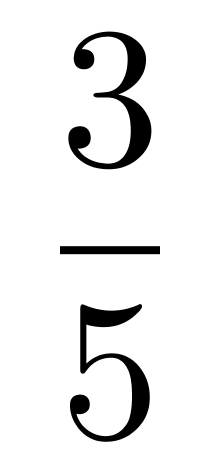
思路:
速度不能叠加,但是时间可以叠加。此题路程相同,可知速度与时间成反比。
(2T上+T下) ÷ (T上+2T下) = 5/4 ,得T上/T下 = 2/1,∴V上/V下 = 1/2
6、小王和小张分别于早上8:00和8:30从甲地出发,匀速骑摩托车前往乙地。10:00小王到达两地的中点丙地,此时小张距丙地尚有5千米。11:00时小张追上小王。则甲、乙两地相距多少千米?
A . 50 B . 75 C . 90 D . 100
思路:
给出路程差就要求出路程比,此题路程比由速度比求出,速度比由时间比求出。
走相同距离时,T王:T张=6:5,V王:V张=5:6,
7、某儿童娱乐场有两条圆形赛车跑道,大圆跑道直径80米,小圆跑道直径60米,两跑道于发车起点A处相切重合。假设甲、乙两辆车同时从A点以相同速度出发(甲跑大圈、乙跑小圈),且此后速度均保持不变。则第一次相距最远时,甲、乙各跑了( )圈。

A.2,3 B. ,2 C.3,2 D.
,2 C.3,2 D. ,2
,2
思路:
周长=2πr,相当于周长为80、60,不管怎么跑,他们的路程都是相同的,因为等速度,等时间。带入求解只有B跑得路程相等。

