【数量关系】第一节：整数特性问题
整数特性法核心公式：
①若A：B = m：n，则A是m的倍数，B是n的倍数，A ±B是m±n的倍数； （m，n互质！）
②若A：B ：C= m：n：p，则A是m的倍数，B是n的倍数，C是p的倍数，A +B+C是m+n+p的倍数；
四大应用：
①当条件中出现比例：m：n或m：n：p （男：女=9:7，男+女是16整数倍）
②当条件中出现分数：m/n
③当条件中出现百分数：% （男比女多40% => 男 = 女(1+40%) => 男：女=7：5）
④当条件中出现倍数：n倍 （A比B多7倍 => A：B = 8：1）
例题：
S1：甲、乙两种商品的价格比是3∶5。如果它们的价格分别下降50元，它们的价格比是4∶7，这两种商品原来的价格各为：
A.300元、500元 B.375元、625元 C.450元、750元 D.525元、875元
在整数特性问题中，特别注意两点：
①、2,4,5,8不适用！除非明确告知能够被精准整除。（人数、零件数）
②、不用讨论小数点。
（女 = 男 * 3.5倍，3.5拆分出0.5 * 7 => 女生人数一定是7的倍数）
例题：
L01：某市服务行业举行业务技能大赛,其中东区参赛人数占总人数的
,西区参赛人数占总人数的
,南区参赛人数占总人数的
,其余的是北区的参赛人员。
结果东区参赛人数的
获奖,西区参赛人数的
获奖,南区参赛人数的
获奖,已知参赛总人数超过100人,不到200人,则参赛总人数为( )
A.120 B.140 C.160 D.180
（9是180的倍数）
L02：老王两年前投资的一套艺术品市价上涨了50%，为尽快出手，老王将该艺术品按市价的八折出售，扣除成交价5%的交易费用后，
发现与买进时相比赚了7万元。问老王买进该艺术品花了多少万元？
A.84 B.42 C.100 D.50
（X*1.5*0.8*0.95=X+7，1.5是3的倍数，遇到乘以X.5的运算，前面×2，后面÷2构造简便运算）
L03：两个派出所某月内共受理案件160起，其中甲派出所受理的案件中有17%是刑事案件，乙派出所受理的案件中有20%是刑事案件，
问派出所在这个月中共受理多少起非刑事案件?
A.48 B.60 C.72 D.96
（17%是命题点，17与100没有公约数）
T01：某农户饲养有肉兔和宠物兔两种不同用途的兔子共计2200只，所有兔子的毛色分为黑、白两种颜色。
肉兔中有87.5%的毛色为黑色，宠物兔有23%的毛色为白色。那么毛色为白色的肉兔至少有多少只？
A、25 B、50 C、100 D、200
（87.5% = 7/8，23% => 23与100互质，设8m+100n=2200 得2200是100倍数，100n是100倍数，所以8m也是100倍数）
L01：办公室有一些黑色和红色的签字笔，最近由于工作需要，每周都会用掉6支黑色签字笔和3支红色签字笔。
3周后整理剩余物资时发现，剩下的红色签字笔的数量是黑色签字笔的2倍。则办公室原有签字笔至少（ ）支。
A . 27 B . 28 C . 29 D . 30
（考点在2倍。9*3 = 27 + 3n = 30）
L02：现有5盒动画卡片，各盒卡片张数分别为：7、9、11、14、17。卡片按图案分为米老鼠、葫芦娃、喜羊羊和灰太狼4种，每个盒内装的是同图案的卡片。
已知米老鼠的卡片只有一盒，而喜羊羊、灰太狼图案的卡片数之和比葫芦娃图案的多1倍。据此可知，图案为米老鼠的卡片张数为？
A . 7 B . 9 C . 14 D . 17
（考点在多1倍，喜羊羊+3n=58，判断3的倍数解题 ）
补充：
A +Ｂ＝Ｃ
A ÷８...1 B÷８...3 ∴ C÷８...4
A ÷８...2 B÷８...4 ∴ C÷８...6
∴ A ÷８...4 B÷８...7 C÷８...3
L05：四人年龄为相邻的自然数列且最年长者不超过30岁，四人年龄之乘积能被2700整除且不能81整除。则四人中最年长者多少岁？
A . 30 B . 29 C . 28 D . 27
（能被2700整除且不能81整除 => 先化简，3^3*100，3^4 => 只能有3个3，不能有4个3）
T03：小李某月请了连续5天的年假，这5天的日期数字相乘为7893600，问他最后一天年假的日期是：
A . 25日 B . 26日 C . 27日 D . 28日
（7893600是3的倍数，不是9的倍数。∴只有一个3，并且是100倍数。）
补充：
①、消3法，判断3的倍数。（0是3的倍数）
7438210 => 0是3的倍数，2+1是3的倍数，7+8是3的倍数，4不是3的倍数。结果÷3余1。
①、消9法，判断9的倍数。
同理。240001÷9余7。
L06：如图，一个正方体的表面上分别写着连续的6个整数，且每两个相对面上的两个数的和都相等，则这6个整数的和为
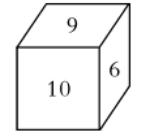
（要么5 6 7 8 9 10，要么 6 7 8 9 10，3个对面的和相等，∴是3的倍数）
G01：每年三月某单位都要组织员工去A、B两地参加植树活动。已知去A地每人往返车费20元，人均植树5棵，去B地每人往返车费30元，人均植树3棵，
设到A地员工有x人，A、B两地共植树y棵，y与x之间满足y=8x-15，若往返车费总和不超过3000元，那么，最多可植树多少棵？
A.489 B.400 C.498 D.500
（偶数 - 奇数 = 奇数）
补充：
y=8X-15 => 8(x-2)+1 => ∴÷8余1
y=8X+15 => ÷8余7
同余问题：
A÷8 ... 3 ，A÷5 ... 3（余同＋余）<=> 40n+3 （所有满足除以8余3和除以5余3的集合，周期是40）
（和同）÷8 ... 1 ，÷5 ... 4（和同＋和）<=> 40n+5
（差同）÷8 ... 6 ，÷5 ... 3（差同－差）<=> 40n-2
口诀：余同＋余，和同＋和，差同－差，公倍数做周期。
余数万能定理：
A ÷ 5 ... 3，=》3,8,13,18（余数周期）
A ÷ 7 ... 4 =》4,11,18（余数周期）
《=》 ÷ 35 ... 18《=》35n+18
G02：某工厂新招了一百多名女工，为她们分配宿舍时发现若每间住6人则有一个房间少1人，
若每间住7人则有一个房间只有1人住，问如果每个房间最多住4人的话，最少需要几个房间？
A.26 B.27 C.28 D.29
（÷6 ... 5 ，÷7 ... 1《=》42n+29）
母题研究
1、两件快递的重量之比是3︰2，去除包装之后的重量之比是9︰5。若包装重量都是120克，则两件快递的重量分别是：
A.390克、260克 B.480克、320克 C.540克、360克 D.630克、420克
思路：
初始是3:2，减去部分后是9:5，说明原来要比9份，5份大，（先放大发现）同乘一个3刚好得到12:8，符合同时减去3等于9:5，
所以3份是120，12份就是480。
2、小张家养了一只大狗和一只小狗。现在，小狗的体重只有大狗的一半。如果两只狗的体重各增加5千克，那么小狗的体重将达到大狗的60%。据此可知，若两只狗的体重各增加10千克，小狗、大狗的体重比将会是
A、1∶2 B、2∶3 C、3∶4 D、4∶5
思路：
同时提高了10千克，相当于溶液中加入了溶质。
初始状态1:2（50%），变成3/5（60%），提高了10%，下一次提高会比10%低。
3、某地区有甲乙丙丁4个派出所。已知上月甲、乙2个派出所的合计出警次数为95次,乙丙丁合计出警140次,乙出警数占四个派出所出警次数总和的7/40,则上月甲派出所出警次数是
思路：
40n - 140 = 尾数法。
甲+7n=95，甲=95-7n（7的倍数）
4、某高校本年度毕业学生3060名，比上年度增长2%。其中本科生毕业数量比上年度减少2%，而研究生数量比上年度增加10%，那么，这所高校本年度本科生毕业数量是：
A.1900 B.1990 C.1960 D.1930
思路：
今年本科 = 去年 *(1-2%)= 去年 * 49/50，所以去年本科是50的倍数，今年本科是49倍数
题目中出现了百分数，而且问题与百分数相关，可以用整除特性法。
6、已知正月初六从某火车站乘车出行旅客人数恰好是正月初五的8.5倍，且恰好比正月初七少9%，则正月初七从该火车站乘车出行的旅客人数至少是：
A.850人 B.1300人 C.1700人 D.3400人
思路：
8.5X = Y*(1-9%) = Y*91/100 ，Y是100的倍数，同时也是8.5倍数 = 17与5的倍数。
T01：某商店规定每4个空啤酒瓶可以换1瓶啤酒，小明家买了24瓶啤酒，他家前后最多能喝到多少瓶啤酒？（ ）
A 30 B 31 C 32 D 33
思路：
每N个空瓶可以换1瓶，一共买了X瓶， X+ [X/(n-1)] 取整数。
7、某老旧写字楼重新装修，需要将原有的窗户全部更换为单价90元每扇的新窗户。已知每7扇换下来的旧窗户可以跟厂商兑换一扇新窗户。全部更换完毕后共花费16560元且剩余4扇旧窗户没有兑换，那么该写字楼一共有多少扇窗户：
A.214 B.184 C.218 D.188
思路：
16560÷90=184，184÷6 = 30
方法二： 7---》1，最后剩4，,总窗数 7n+4 =》 ÷7...4
8、在一次马拉松比赛中，某国运动员包揽了前四名，他们佩戴的参赛号码很有趣运动员甲的号码加4，乙的号码减4，丙的号码乘4，丁的号码除以8，所得的数字都一样。这四个号码中有1个三位数号码，2个两位数号码，1个一位数号码，且其中一位运动员在比赛中取得的名次也与自己的号码相同。那么其中三位数的号码为
A、1120 B、128 C、256 D、512
思路：
所得数字设成4X，
9、瓶中装有浓度为20%的酒精溶液为1000克，现在又分别倒入200克和400克的A、B两种酒精溶液，瓶里的溶液浓度变为15%。已知A种酒精溶液的浓度是B种酒精溶液浓度的2倍。那么A种酒精溶液的浓度是多少？
A.5% B.6% C.8% D.10%
思路：
中间错误结果一定出现在选项中。
10、某机关事务处集中采购了一批打印纸，分发给各职能部门。如果按每个部门9包分发，则多6包；如果按每个部门11包分发，则有1个部门只能分到1包。这批打印纸的数量是（）。
· A.87包 B.78包 C.69包 D.67包
思路：
÷9...6 与 ÷11...1
11、将2万本书籍分给某希望小学9个班的学生。在9个班中，其中1个班有学生32人，其余8个班人数相同且在40到50人之间。如每名学生分到的书本数相同，问每人分到了多少本书？
A.40 B.50 C.60 D.80
思路：
假设每人y本，32Y+8XY = 20000，4Y+XY=2500，(4+X)*Y=2500
Y必须是2500的整数倍。
12、某单位原拥有中级及以上职称的职工占职工总数的62.5%。现又有2名职工评上中级职称，之后该单位拥有中级及以上职称的人数占总人数的。则该单位原来有多少名职称在中级以下的职工？
A.68 B.66 C.62 D.60
思路：
中下/总 = 3/8 ，中下-2/总 = 4/11，减2后是4的倍数
