Lyndon 理论学习笔记

upd：修了一些不严谨的表述。

字符串，太深刻了 /kk

引理、结论的证明建议不要跳过，很多问题的思考过程和引理、结论的证明过程是相通的。

定义

下标从 1 开始。

\(+\) 是字符串拼接。

\(|s|\) 表示 \(s\) 的长度。

\(s_i\) 表示 \(s\) 的第 \(i\) 个字符。

\(s^k\) 表示 \(k\) 个 \(s\) 拼接的结果。

字符串间的大小关系用字典序比较，空串小于任何串。

Lyndon 分解

Duval 算法

字符串 \(s\) 是 Lyndon 串当且仅当 \(s\) 小于其每个非空真后缀。

有的文章里的“简单串”就是 Lyndon 串。

若字符串 \(s=w_1+\dots+w_k\)，且 \(w_1\dots w_k\) 都是 Lyndon 串，且 \(w\) 字典序单调不增（\(w_i\ge w_{i+1}\)），

则 \(w_1\dots w_k\) 是 \(s\) 的 Lyndon 分解。

引理 1：\(s\) 字典序最小的非空后缀为 \(w_k\)。

证明：任意 \(w_i\) 都小于其每个非空真后缀，所以从 \(w_i\) 起头一定比从 \(w_i\) 中间起头（也就是以 \(w_i\) 的某个非空真后缀起头）优，

而 \(w_k\) 小于等于 \(w_i(i\ne k)\)，所以从 \(w_k\) 起头一定比从 \(w_i\) 起头优，则肯定从 \(w_k\) 起头，这个后缀就是 \(w_k\)。

引理 2：Lyndon 分解唯一存在。

证明：由引理 1 可以唯一确定 \(w_k\)，而 \(w_1\dots w_{k-1}\) 一定是 \(s\) 去掉 \(w_k\) 后的串的 Lyndon 分解，于是可以确定 \(w_{k-1}\)，

以此类推，可以唯一确定 \(w_1\dots w_k\)。

由引理 2 可以轻松得到一个 \(O(n^2)\) 的 Lyndon 分解算法，但是这显然不是我们想要的。

Duval 算法可以 \(O(n)\) 求出 Lyndon 分解。

定义字符串 \(s\) 是近似 Lyndon 串，当且仅当 \(s=w^k+w'\)，其中 \(w\) 是任意 Lyndon 串，\(k\ge 1\)，\(w'\) 是 \(w\) 的前缀（可以空）。

划分 \(s=s_1+s_2+s_3\)，其中 \(s_1\) 的 Lyndon 分解已经得出，\(s_2\) 是一个近似 Lyndon 串，\(s_3\) 无要求，

初始 \(s_1\) 为空，\(s_2\) 是 \(s\) 的第一个字符（单字符肯定是近似 Lyndon 串），\(s_3\) 是 \(s\) 去掉第一个字符后的串，

现在需要调整划分方案，使得 \(s_1=s\)，\(s_2=s_3=\varnothing\)。

设 \(s_2=w^k+w'\)，\(x=w_{|w'|+1}\)，尝试每次去掉 \(s_3\) 开头的字符 \(y\) 加到 \(s_2\) 末尾，考虑 \(x,y\) 的关系：

• \(x=y\)：\(w^k+w'+x\) 仍是近似 Lyndon 串，无需调整划分方案，更新一下 \(w'\) 即可。
• \(x<y\)：\(w^k+w'+y\) 是 Lyndon 串。

证明：设 \(t=w^k+w'+y\)。需要证明 \(t\) 字典序最小的非空后缀是 \(t\) 本身。
引理 1 已经证过从 \(w\) 起头一定比从 \(w\) 中间起头优，
由 \(x<y\) 得 \(w'+y>w\)，而从第 \(i(i\ne 1)\) 个 \(w\) 起头比从第一个 \(w\) 起头先走到 \(w'+y\)，
则从第一个 \(w\) 起头一定比从第 \(i\) 个 \(w\) 起头优，则肯定从第一个 \(w\) 起头，这个后缀就是 \(t\) 本身。

Lyndon 串肯定也是近似 Lyndon 串，所以也无需调整划分方案，

但 \(w'+y\) 并不是 \(w\) 的前缀，所以需要更新 \(w=t\)，\(w'=\varnothing\)。

• \(x>y\)：\(w^k+w'+y\) 啥也不是，必须调整划分方案。把 \(k\) 个 \(w\) 划分进 \(s_1\)，令 \(s_2\) 为 \(s_1\) 后第一个字符，\(s_3\) 为剩下的串即可。

\(s_3\) 为空时像 \(x>y\) 一样调整划分方案（把 \(k\) 个 \(w\) 划分进 \(s_1\)，令 \(s_2\) 为 \(s_1\) 后第一个字符，\(s_3\) 为剩下的串），

以此法不断去掉 \(s_3\) 开头的字符加到 \(s_2\) 末尾，可以发现 \(s_1\) 的长度一直在增加，最终一定能达到 \(s_1=s\)。

实现的时候一般用类似最小表示法的三指针，维护 \(s_2\) 开头 \(i\)，\(s_3\) 开头 \(j\)，以及 \(k=j-|w|\)（\(s_k=x\)）。

//洛谷 P6114 【模板】Lyndon 分解
#include <cstdio>
#include <cstring>
int n, z;
char a[10000050];
int main()
{
    scanf("%s", a + 1), n = strlen(a + 1);
    int i = 1, j, k;
    while (i <= n)
    {
        j = i + 1, k = i;
        while (j <= n)
        {
            if (a[j] == a[k])
                ++j, ++k;
            else if (a[j] > a[k])
                ++j, k = i;
            else
                break;
        }
        while (i <= k)
            z ^= i + j - k - 1, i += j - k; //[i, i + j - k - 1] 是分解出的一个 Lyndon 串
    }
    printf("%d", z);
    return 0;
}

所以这玩意有啥用？

最小表示法

给定字符串 \(s\)，求与 \(s\) 循环同构的字典序最小的串。（假设你不会正常的最小表示法）

想一想，怎么做

设 \(t=s+s\)，则需要找出 \(t\) 的长度为 \(n\) 的最小子串。

对 \(t\) Lyndon 分解，引理 1 证过从 \(w_i\) 中间起头不优，且越靠后的 \(w_i\) 越优，

所以最优起头位置为最后一个 \(w_i\)，使得 \(w_i\) 左端点后有不少于 \(n\) 个字符。

//洛谷 P1368 【模板】最小表示法 
#include <cstdio>
int n, m, z, a[10000050];
int main()
{
    scanf("%d", &m), n = m << 1;
    for (int i = 1; i <= m; ++i)
        scanf("%d", a + i), a[m + i] = a[i];
    int i = 1, j, k;
    while (i <= n)
    {
        j = i + 1, k = i;
        while (j <= n)
        {
            if (a[j] == a[k])
                ++j, ++k;
            else if (a[j] > a[k])
                ++j, k = i;
            else
                break;
        }
        while (i <= k)
        {
            if (i <= m + 1)
                z = i;
            i += j - k;
        }
    }
    for (int i = z; i < z + m; ++i)
        printf("%d ", a[i]);
    return 0;
}

k 划分见过没

给定字符串 \(s\) 和整数 \(k\)，把 \(s\) 划分为不超过 \(k\) 个串 \(c_1\dots c_m(m\le k)\)，求 \(\max c_i\) 的最小值。

想一想，怎么做

对 \(s\) Lyndon 分解得到 \(s=w_1^{m_1}+\dots+w_z^{m_z}\)，则 \(\max c_i\) 有多大取决于其分到多少个 \(w_1\)，

根据鸽巢原理，\(\max c_i\) 至少分到 \(\left\lceil\dfrac {m_1}k\right\rceil\) 个 \(w_1\)，

若 \(k\mid m_1\)，则每个 \(c_i\) 都分到 \(m_1/k\) 个 \(w_1\)，最后一个 \(c_i\) 还要承包 \(w_2^{m_2}+\dots+w_z^{m_z}\)，

于是 \(\max c_i\) 就是最后一个 \(c_i\)，即 \(w_1^{m_1/k}+w_2^{m_2}+\dots+w_z^{m_z}\)

否则有些 \(c_i\) 分到了 \(\left\lceil\dfrac {m_1}k\right\rceil\) 个 \(w_1\)（A 类），有些 \(c_i\) 分到了 \(\left\lfloor\dfrac {m_1}k\right\rfloor\) 个 \(w_1\)（B 类），

令最后一个 \(c_i\) 属于 B 类，这样其承包 \(w_2^{m_2}+\dots+w_z^{m_z}\) 后 \(\max c_i\) 还是之前的一个 A 类，即 \(w_1^{\left\lceil\frac {m_1}k\right\rceil}\)。

k 划分见过没 2（对每个后缀 Lyndon 分解）

设 \(f(s,k)\) 表示对 \(s,k\) 做《k 划分见过没》的结果，

给定字符串 \(s\)，有 \(q\) 次询问，每次给定 \(x,y\)，设 \(t\) 为 \(s\) 长度为 \(x\) 的后缀，求 \(f(t,y)\)。

想一想，怎么做

如果能对所有后缀 Lyndon 分解，那这题就做完了。

实际上只需要对每个后缀求出其分解出的 \(w_1\)，因为 \(w_2\dots w_k\) 一定是这个后缀去掉 \(w_1\) 后的串的 Lyndon 分解。

结论：对于 \(s\) 以 \(i\) 开头的后缀 \(S_i\)（\(S_{n+1}=\varnothing\)）求出最小的 \(j\) 使得 \(j>i,S_j<S_i\)，则 \(S_i\) 分解出的 \(w_1\) 为 \(s\) 从 \(i\) 到 \(j-1\) 的子串。

证明：只需要证 \(w_1\) 是 Lyndon 串，且 \(w_1\ge w_2\)，剩下的归纳即可。

• \(w_1\) 是 Lyndon 串：考虑反证法，设 \(w_1\) 有非空后缀 \(t\) 小于 \(w_1\)，而 \(S_i\) 以 \(t\) 起头的后缀 \(X\) 又大于 \(S_i=Y\)，所以 \(t\) 肯定是 \(w_1\) 的真前缀。对 \(X\) 和 \(Y\) 同时去掉前缀 \(t\)，得到 \(S_j=X'\) 大于 \(S_i\) 以 \(w_1\) 的某个非空后缀 \(t'\) 起头的后缀 \(Y'\)，则 \(Y'<X'<S_i\)，这样 \(w_2\) 就应该以 \(t'\) 开头。但 \(w_2\) 并没有以 \(t'\) 开头，所以 \(w_1\) 是 Lyndon 串。

• \(w_1\ge w_2\)：考虑反证法，设 \(w_1<w_2\)。而 \(S_i>S_j\)，所以 \(w_1\) 肯定是 \(w_2\) 的真前缀。对 \(S_i\) 和 \(S_j\) 同时去掉 \(w_1\) 前缀，得到 \(S_j\) 大于 \(S_i\) 以 \(w_2\) 的某个非空后缀 \(t\) 起头的后缀，这样 \(w_3\) 就应该以 \(t\) 开头。但 \(w_3\) 并没有以 \(t\) 开头，所以 \(w_1\ge w_2\)。

求出 SA 后扫描线 + set 即可对每个 \(S_i\) 求出最小的 \(j\) 使得 \(j>i,S_j<S_i\)，然后就做完了。

HDU 6761 Minimum Index（对每个前缀 Lyndon 分解）

给定字符串 \(s\)，求 \(s\) 每个前缀的最小非空后缀。

想一想，怎么做

考虑在 Duval 算法的过程中求出 \(s_1+s_2\) 每个时刻的最小非空后缀。

若 \(s_2=w\)，则最小非空后缀为 \(w\)。

若 \(s_2=w^k+w'\)，此时引理 1 的分析不再完全适用：从 \(w\) 中间起头仍然不如从 \(w\) 起头，

但是从 \(w'\) 中间起头可能优于从 \(w'\) 起头，因为 \(w'\) 不是 Lyndon 串。

所以只有可能从 \(w\) 起头或从 \(w'\) 中间起头，可以发现去掉后 \(|w|\) 个字符后答案不变，而去掉后 \(|w|\) 个字符后的答案早已求出。

可以发现过程中 \(s_1+s_2\) 会覆盖每个前缀，所以这就够了。

实际上本题对每个前缀求出了其 Lyndon 分解出的最后一个串 \(w_k\)，可以由此得到每个前缀的 Lyndon 分解。

//HDU 6761 Minimum Index
#include <cstdio>
#include <cstring>
#define M 1000000007
int T, n, z[10000050];
char a[10000050];
int main()
{
    scanf("%d", &T);
    while (T--)
    {
        scanf("%s", a + 1), n = strlen(a + 1);
        int i = 1, j, k;
        while (i <= n)
        {
            j = i + 1, k = i;
            while (1)
            {
                if (k == i)
                    z[j - 1] = i;
                else
                    z[j - 1] = z[k - 1] + j - k;
                if (j > n)
                    break;
                if (a[j] == a[k])
                    ++j, ++k;
                else if (a[j] > a[k])
                    ++j, k = i;
                else
                    break;
            }
            while (i <= k)
                i += j - k;
        }
        int Z = 0;
        for (int i = 1, o = 1; i <= n; ++i)
            Z = (Z + 1ll * z[i] * o) % M, o = o * 1112ll % M;
        printf("%d\n", Z);
    }
    return 0;
}

洛谷 P5334 [JSOI2019] 节日庆典

给定字符串 \(s\)，求 \(s\) 每个前缀的最小表示法。

想一想，怎么做

求某个串 \(s\) 的最小表示，实际上就是求 \(s\) 的一个非空后缀 \(S\)，设 \(s\) 去掉 \(S\) 后得到的前缀为 \(P\)，求 \(\min(S+P)\)。

直接取 \(s\) 的最小非空后缀作为 \(S\) 肯定不行，比如 \(s=\texttt{baa}\) 时，\(s\) 的最小非空后缀为 \(\texttt{a}\)，取 \(S=\texttt{a}\) 得到 \(S+P=\texttt{aba}\)，

但是取 \(S=\texttt{aa}\) 可以得到 \(S+P=\texttt{aab}\)，比直接取最小非空后缀作为 \(S\) 要优。

然而，我们仍然可以沿用上一题求每个前缀的最小非空后缀的思路，在 Lyndon 分解的过程中求解。

考虑在 Lyndon 分解的过程中求出 \(s_1+s_2\) 每个时刻的最小表示法。

若 \(s_2=w\)，取 \(S=w\)。

若 \(s_2=w^k+w'\)，此时去掉后 \(|w|\) 个字符后最优 \(S\) 可能会变，

因为可能取 \(S=w^k+w'\) 最优，但是去掉后 \(|w|\) 个字符后就取不到 \(S=w^k+w'\) 了，

所以需要考虑去掉后 \(|w|\) 个字符后的最优 \(S\)（下文设为 \(T\)）和 \(w^k+w'\)，

如果 \(|T|>|w^{k-1}+w'|\)，那么此时的最优 \(S\) 根本取不到 \(T\)，直接取 \(w^k+w'\) 即可，

否则 \(T\) 要么从某个 \(w\) 起头，要么从 \(w'\) 的某个后缀起头，

结论：\(|T|\le|w^{k-1}+w'|\) 时，\(T\) 一定是 \(w^k+w'\) 的前缀。

证明：若 \(T\) 从某个 \(w\) 起头，则 \(T\) 形如 \(w^p+w'(p<k)\)，一定是 \(w^k+w'\) 的前缀。

若 \(T\) 是 \(w'\) 的某个后缀 \(t\)，则 \(t\) 一定是 \(w\) 的前缀，

否则 \(t\) 和 \(w\) 的比较在 \(|t|\) 前就结束了，若 \(t<w\) 则 \(w\) 不是 Lyndon 串，若 \(t>w\) 则 \(T\) 不应该从 \(t\) 起头，而应该从 \(w\) 起头。

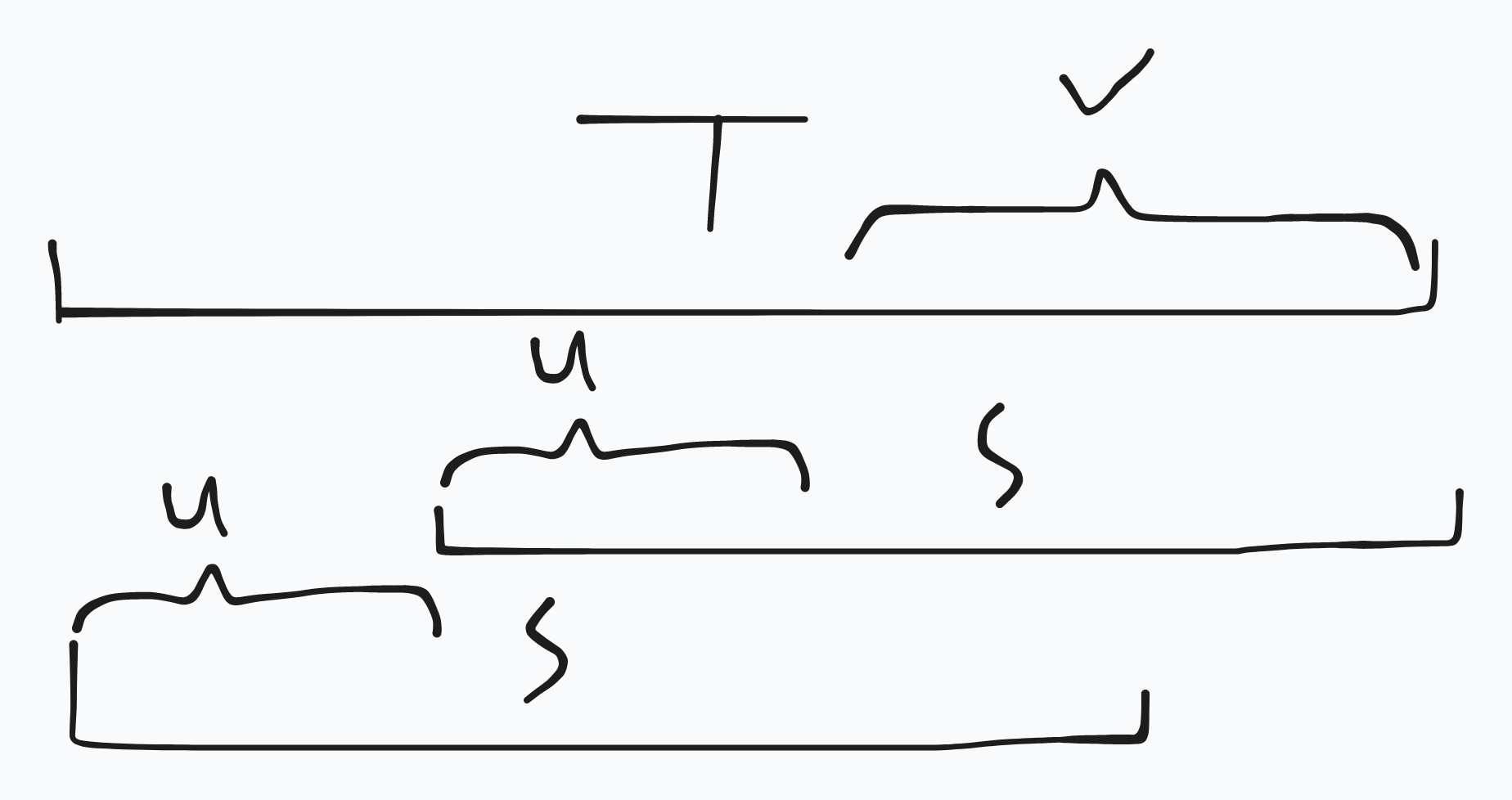
所以 \(w^k+w'\) 和 \(T\) 的关系形如下图：

现在需要比较从 \(\uparrow_A\) 和 \(\uparrow_B\) 开头的两种答案，

它们的前 \(|T|\) 个字符相同，所以只需要比较从 \(\downarrow_A\) 和 \(\downarrow_B\) 开头的两种答案，

此时只需要求原串与后缀的 LCP，预处理 Z 函数即可。

//洛谷 P5334 [JSOI2019] 节日庆典 
#include <cstdio>
#include <cstring>
#include <algorithm>
#define M 1000000007
using namespace std;
int n, z[10000050], Z[10000050];
char a[10000050];
int main()
{
    scanf("%s", a + 1), n = strlen(a + 1);
    z[1] = n;
    for (int i = 2, l = 0, r = 0; i <= n; ++i)
    {
        if (i <= r)
            z[i] = min(z[i - l + 1], r - i + 1);
        while (i + z[i] <= n && a[i + z[i]] == a[z[i] + 1])
            ++z[i];
        if (i + z[i] - 1 > r)
            l = i, r = i + z[i] - 1;
    }
    int i = 1, j, k;
    while (i <= n)
    {
        j = i + 1, k = i;
        while (1)
        {
            if (!Z[j - 1]) // 这题在最小表示法相同时要输出最小开头，所以取每个前缀第一次被 s1+s2 覆盖时的答案
            {
                if (k == i || k - Z[k - 1] > k - i) // s2=w 时直接取 w，|T|>|w^(k-1)+w'| 时直接取 w^k+w'
                    Z[j - 1] = i;
                else //|T|<=|w^(k-1)+w'|，用 Z 函数比较两种答案即可
                {
                    bool F;
                    int S = i, T = Z[k - 1] + j - k;
                    int A = S + j - T, B = 1;
                    if (z[A] >= j - A)
                    {
                        A = 1, B += j - A;
                        if (z[B] >= T - B)
                            F = S < T;
                        else
                            F = a[z[B] + 1] < a[B + z[B]];
                    }
                    else
                        F = a[A + z[A]] < a[z[A] + 1];
                    if (F)
                        Z[j - 1] = S;
                    else
                        Z[j - 1] = T;
                }
            }
            if (j > n)
                break;
            if (a[j] == a[k])
                ++j, ++k;
            else if (a[j] > a[k])
                ++j, k = i;
            else
                break;
        }
        while (i <= k)
            i += j - k;
    }
    for (int i = 1; i <= n; ++i)
        printf("%d ", Z[i]);
    return 0;
}

最小后缀族

考虑这样一个问题：给定字符串 \(s\)，每次询问一个字符串 \(T\)，求 \(s\) 的一个后缀 \(S\)（可空）使得 \(S+T\) 最小。

称可能成为最优 \(S\) 的后缀为 \(s\) 的有效后缀，\(s\) 的最小后缀族 \(SS(s)\) 就是 \(s\) 的所有有效后缀组成的集合。

引理 3：若 \(S\)，\(T\) 都是 \(s\) 的有效后缀且 \(|S|<|T|\)，则 \(S\) 是 \(T\) 的 border 且 \(2|S|\le|T|\)。

证明：首先一定有 \(S<T\)，否则 \(S\) 与 \(T\) 的比较在 \(|S|\) 前就结束了，\(S\) 不可能是有效后缀，

而且 \(S\) 一定是 \(T\) 的前缀，否则 \(S\) 与 \(T\) 的比较在 \(|S|\) 前就结束了，\(T\) 不可能是有效后缀，

而 \(S\) 明显是 \(T\) 的后缀，所以 \(S\) 是 \(T\) 的 border。

考虑反证法，若 \(2|S|>|T|\)，设 \(S\) 长度为 \(|T|-|S|\) 的前缀为 \(u\)，则 \(T\) 一定可以写成 \(u^2+v\)，而 \(S=u+v\)。

若存在字符串 \(y\) 使得 \(u+v+y<v+y\)，则 \(u^2+v+y<u+v+y\)，\(S=u+v\) 要么比 \(T=u^2+v\) 劣，要么比 \(v\) 劣，\(S\) 一定不是有效后缀，

但是 \(S\) 确实是有效后缀，所以 \(2|S|\le|T|\)。

由引理 3 可知，\(|SS(s)|=O(\log |S|)\)。

引理 4：有效后缀一定形如 \(S_i=w_i^{c_i}+\dots+w_k^{c_k}\)（\(S_{k+1}=\varnothing\)）。

证明：引理 1 已经证过从 \(w_i\) 中间起头不优，只需要证一定从第一个 \(w_i\) 起头，

类似引理 3 后半部分的证法，\(w_i^x+\dots+w_k^{c_k}(x\ne c_i)\) 要么比 \(w_i^{x+1}+\dots+w_k^{c_k}\) 劣，要么比 \(w_i^{x-1}+\dots+w_k^{c_k}\) 劣，

则不从第一个 \(w_i\) 起头肯定不优，所以一定从第一个 \(w_i\) 起头。

\(SS(s)\) 咋求呢？\(\newcommand{\L}{\lambda}\)

考虑 Duval 算法过程中第一次 \(s_3=\varnothing\) 的时刻，设此时 \(s_2=w_{\L}^{c_{\L}}+w_{\L}'\)，

可以发现 \(S_{\L}=w_{\L}^{c_{\L}}+w_{\L}'\)，\(S_{\L+1}=w_{\L}'\)，所以 \(S_{\L+1}\) 是 \(S_{\L}\) 的前缀，

考虑 Duval 算法的过程，从 \(|s_2|=1\) 开始，每次往 \(s_2\) 后加一个字符后 \(s_2\) 一直是近似 Lyndon 串，

所以 \(s_2\) 的每个前缀都是近似 Lyndon 串，\(S_{\L+1}=w_{\L}'\) 明显是 \(s_2\) 的前缀，于是 \(S_{\L+1}\) 也是近似 Lyndon 串，

下次 \(s_3=\varnothing\) 时 \(s_2=S_{\L+1}=w_{\L+1}^{c_{\L+1}}+w_{\L+1}'\)，\(S_{\L+2}=w_{\L+1}'\)，所以 \(S_{\L+2}\) 是 \(S_{\L+1}\) 的前缀,

以此类推，\(\forall i\ge\L\)，\(S_{i+1}\) 是 \(S_i\) 的前缀，并且每次 \(s_3=\varnothing\) 时的 \(s_2\) 取遍 \(S_i(i\ge\L)\)。

\(\forall i<\L,S_i=w_i^{c_i}+w_i'+s_3,S_{i+1}=w_i'+s_3\)，而 \(s_3<w_i\)，所以 \(S_{i+1}\) 肯定不是 \(S_i\) 的前缀。于是：

引理 5：\(S_{i+1}\) 是 \(S_i\) 的前缀当且仅当 \(i\ge\L\)。

所以，结合引理 3 可以确定，\(\forall i<\L,S_i\notin SS(s)\)。实际上 \(\forall i\ge\L,S_i\in SS(s)\)，接下来将说明这一点。

回到原问题：给定字符串 \(s\)，每次询问一个字符串 \(T\)，求 \(s\) 的一个后缀 \(S_i\)（可空）使得 \(S_i+T\) 最小。

首先 \(S_i\in SS(s)\)，所以 \(i\ge\L\)。对于 \(i\ge\L\) 设 \(w_i=S_{i+1}+y_i\)，\(x_i=y_i+S_{i+1}\)，则 \(S_i=S_{i+1}+x_i^{c_i}\)。

（笑点解析：论文这里 typo 了，写成了 \(S_i=S_{i+1}+y_i\)，模了半天没模明白）

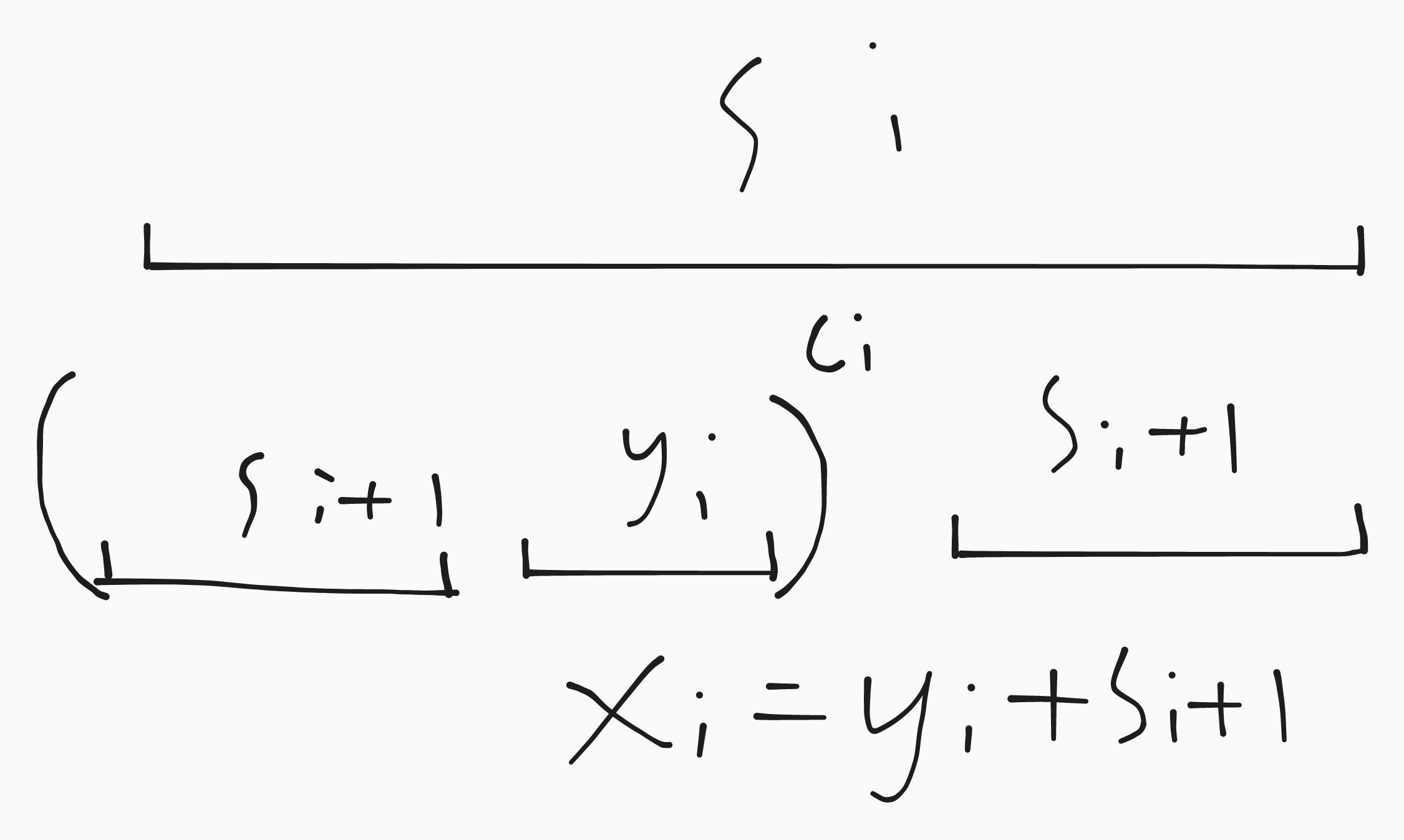
引理 6：\(\forall i\in[\L,k-1],x_i^{\infty}>x_{i+1}^{\infty}\)

证明：首先 \(x_i^{\infty}>y_i\)，只需证 \(y_i>x_{i+1}^{\infty}\)。

两边同时在前面拼接 \(S_{i+1}\)，左边 \(S_{i+1}+y_i=w_i\)，右边

\[\begin{aligned} &S_{i+1}+x_{i+1}^{\infty}\\ =&S_{i+1}+(y_{i+1}+S_{i+2})^{\infty}\\ =&S_{i+2}+x_{i+1}^{c_{i+1}}+(y_{i+1}+S_{i+2})^{\infty}\\ =&S_{i+2}+(y_{i+1}+S_{i+2})^{c_{i+1}}+(y_{i+1}+S_{i+2})^{\infty}\\ =&S_{i+2}+(y_{i+1}+S_{i+2})^{\infty}\\ =&(S_{i+2}+y_{i+1})^{\infty}+S_{i+2}\\ =&w_{i+1}^{\infty}+S_{i+2} \end{aligned} \]

字符串推式子见过没（

此时只需证 \(w_i>w_{i+1}^{\infty}\)。

根据引理 5 的证明过程，\(S_{i+1}\) 是 \(w_i\) 的前缀，那么 \(w_{i+1}\) 肯定也是 \(w_i\) 的前缀，

设 \(w_i=w_{i+1}^k+t\)，其中 \(w_{i+1}\) 不是 \(t\) 的前缀，而 \(w_i\) 是 Lyndon 串，所以 \(t>w_i\)，

而且 \(w_{i+1}\) 不是 \(t\) 的前缀，所以 \(t\) 与 \(w_i\) 的比较在前 \(|w_{i+1}|\) 位就能结束，所以 \(t>w_{i+1}^{\infty}\)，

两边同时在前面拼接 \(w_{i+1}^k\)，得到 \(w_{i+1}^k+t>w_{i+1}^k+w_{i+1}^{\infty}\)，所以 \(w_i>w_{i+1}^{\infty}\)。

再次回到原问题：对给定的 \(T\)，考虑比较 \(S_i+T\) 和 \(S_{i+1}+T\)。

首先 \(S_i+T=S_{i+1}+x_i^{c_i}+T\)，只需比较 \(x_i^{c_i}+T\) 和 \(T\)。

（笑点解析：这里论文又 typo 了，翻转后缀见过没）

结论：\(x_i^{c_i}+T<T\) 当且仅当 \(x_i^{\infty}<T\)。

证明：设 \(T=(x_i^{c_i})^k+t\)，其中 \(x_i^{c_i}\) 不是 \(t\) 的前缀，\(k\) 可能等于 \(0\)，则需要比较 \((x_i^{c_i})^{k+1}+t\) 和 \((x_i^{c_i})^k+t\)，

由于 \(x_i^{c_i}\) 不是 \(t\) 的前缀，前 \(|(x_i^{c_i})^{k+1}|\) 位一定能比出结果，所以用 \(x_i^{\infty}\) 与 \(T=(x_i^{c_i})^k+t\) 一定能比出相同的结果。

所以 \(S_i+T<S_{i+1}+T\iff x_i^{c_i}+T<T\iff x_i^{\infty}<T\)，

\(x_i^{\infty}\) 单调减，所以一定存在 \(p\) 使得 \(\forall i<p,x_i^{\infty}>T\iff S_i+T>S_{i+1}+T,\forall i\ge p,x_i^{\infty}<T\iff S_i+T<S_{i+1}+T\)，

可以发现答案就是 \(S_p+T\)，二分求出 \(p\) 即可。

注意到 \(\forall i\ge\L\)，\(S_i\) 都有可能成为 \(S_p\)，这样就证明了上面提出的 \(\forall i\ge\L,S_i\in SS(s)\)。

下文将求出的 \(S_p\) 称为“后接 \(T\) 的最小后缀”。

所以这玩意有啥用？

最大后缀

给定字符串 \(s\)，求 \(s\) 每个前缀的最大后缀。

（笑点解析：论文原题是求 \(s\) 的最大后缀）

想一想，怎么做

先做一下论文原题：

首先反转字母表之后就是求最小后缀了吗？并不是，

比如后缀 \(S\) 是后缀 \(T\) 的前缀时应该取较长的 \(T\)，但是反转字母表后求最小后缀会取到较短的 \(S\)，

考虑修补这个做法，反转字母表后设一个极大字符 \(\texttt{#}\)，然后求出后接 \(\texttt{#}\) 的最小后缀，这样就可以取到较长的 \(T\) 了，

\(\texttt{#}\) 肯定大于所有 \(x_i\)，所以后接 \(\texttt{#}\) 的最小后缀就是 \(S_{\L}\)。

（但是根本没必要这么做，直接在 \(s\) 后面接一个 \(\texttt{#}\)，然后求最小后缀就行了……）

考虑求 \(s\) 每个前缀的最大后缀。

肯定不能把每个前缀后面都接上 \(\texttt{#}\) 做一次，所以考虑对每个前缀求出 \(S_{\L}\)，

考虑之前几个题的做法，\(s_1+s_2\) 会覆盖所有前缀，所以某个前缀第一次被 \(s_1+s_2\) 覆盖时，\(s_2\) 就是这个前缀的 \(S_{\L}\)。

洛谷 P5334 [JSOI2019] 节日庆典（求每个前缀的 SS）

再 放 送

给定字符串 \(s\)，求 \(s\) 每个前缀的最小表示法。

想一想，怎么做

求某个串 \(s\) 的最小表示，实际上就是求 \(s\) 的一个非空后缀 \(S\)，设 \(s\) 去掉 \(S\) 后得到的前缀为 \(P\)，求 \(\min(S+P)\)。

根据引理 5，对于有效后缀 \(S_i\) 和不是有效后缀的后缀 \(T\)（明显有 \(S_i<T\)），\(S_i\) 一定不是 \(T\) 的前缀，

所以 \(S_i\) 和 \(T\) 的比较在 \(|S_i|\) 前就结束了，最优 \(S\) 一定不会取到 \(T\)。

所以求最优 \(S\) 只需要考虑有效后缀，现在只需要对每个前缀求出所有有效后缀。

设 \(P_i\) 表示 \(s\) 以 \(i\) 结尾的前缀，设 \(SS(P_i)\) 表示 \(P_i\) 的所有有效后缀的起头位置集合，

根据有效后缀的定义，可以发现 \(SS(P_i)-SS(P_{i-1})\) 要么为 \(\{i\}\)，要么为 \(\varnothing\)，

于是考虑从 \(SS(P_{i-1})\) 递推到 \(SS(P_i)\)：

考虑从短到长依次加入 \(SS(P_{i-1})\) 中每个起头位置对应的后缀 \(S_j+s_i\)，

加入 \(S_j+s_i\) 时，设加入的上一个后缀为 \(S_p+s_i\)，首先 \(S_p\) 肯定是 \(S_j\) 的前缀，设 \(S_j\) 的第 \(|S_p|+1\) 个字符为 \(x\)，

若 \(x<s_i\)，则前 \(|S_p+s_i|\) 位就能比出 \(S_p+s_i<S_j+s_i\)，那肯定就不用加入 \(S_j+s_i\) 了，

若 \(x=s_i\) 且 \(2|S_p+s_i|\le|S_j+s_i|\)，则 \(S_p+s_i\) 有可能是有效后缀（满足引理 3 不一定是有效后缀），

不管 \(S_p+s_i\) 是不是有效后缀，保留 \(S_p+s_i\) 对复杂度和正确性都没影响，直接加入 \(S_j+s_i\) 即可，

否则 \(S_p+s_i\) 不可能是有效后缀（不满足引理 3 一定不是有效后缀），删除 \(S_p+s_i\) 后加入 \(S_j+s_i\) 即可。

再之前加入的后缀同样满足引理 3，所以它们也有可能是有效后缀，保留它们对复杂度和正确性都没影响，所以不用管它们。

上面的“有可能”使得维护出的 \(SS'(P_i)\) 只是满足引理 3 的一个后缀集合，而不是真正的有效后缀集合 \(SS(P_i)\)，

但 \(SS(P_i)\) 肯定是 \(SS'(P_i)\) 的子集，而且 \(SS'(P_i)\) 的大小也是 \(O(\log|s|)\)，这就够了。

\(SS'(P_i)\) 中的后缀满足引理 3，所以仍然可以用 Z 函数比较两个后缀对应的答案。总复杂度 \(O(|s|\log|s|)\)。

甚至不需要 Lyndon 分解……

#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
int n, z[3000050];
char a[3000050];
vector<int> S[3000050];
int main()
{
    scanf("%s", a + 1), n = strlen(a + 1);
    z[1] = n;
    for (int i = 2, l = 0, r = 0; i <= n; ++i)
    {
        if (i <= r)
            z[i] = min(z[i - l + 1], r - i + 1);
        while (i + z[i] <= n && a[i + z[i]] == a[z[i] + 1])
            ++z[i];
        if (i + z[i] - 1 > r)
            l = i, r = i + z[i] - 1;
    }
    S[1].push_back(1), printf("1 ");
    for (int i = 2; i <= n; ++i)
    {
        S[i].push_back(i);
        for (auto j : S[i - 1])
        {
            if (a[i] < a[j + i - S[i].back()])
                continue;
            if (a[i] > a[j + i - S[i].back()] || i - j + 1 < i - S[i].back() + 1 << 1)
                S[i].pop_back(); //S_p+s_i 不可能是有效后缀，删除 S_p+s_i
            S[i].push_back(j);
        }
        int Z = S[i][0];
        for (int j = 1; j < S[i].size(); ++j)
        {
            int T = S[i][j];
            int A = T + i - Z + 1, B = 1;
            if (z[A] >= i - A + 1)
            {
                A = 1, B += i - A + 1;
                if (z[B] >= Z - B || a[z[B] + 1] < a[B + z[B]])
                    Z = T;
            }
            else if (a[A + z[A]] < a[z[A] + 1])
                Z = T;
        }
        printf("%d ", Z);
    }
    return 0;
}

洛谷 P5210 [ZJOI2017] 线段树（求区间 SS）

但是我不小心狂暴吸入了过多例题的题解，等我忘了之后重新思考一遍再写吧，，，

Lyndon 数组与 Runs

这是一级标题哦！跟上面的 Lyndon 分解就没什么关系了

我去咋这么多引理……等我看会