关于最短路
前置知识：存图
又开了个史前巨坑
单源最短路
题意：给定源点 $s$，求 $s$ 到图上每个点的最短路径长度。
我们设当前已知的 $s\rightarrow i$ 的最短路长度为 $dis_i$。
我们考虑如何更新一条不那么优的路径。
比如下面 $1 \rightarrow 3$ 的最短路径（$1$ 是源点）
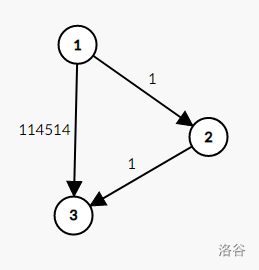
很显然，最短路径是 $1 \rightarrow 2 \rightarrow 3$，长度为 $2$。
目前 $dis_2=1,dis_3=114514$。
那么我们就要用 $2 \rightarrow 3$ 的 $1$ 来更新不那么优的 $dis_3$。
也就是 $dis_3=min(dis_3,dis_2+w(2,3))$。
（$w(u,v)$ 表示 $u,v$ 之间的边权长度）。
用大白话，如果从 2 绕更短就从从 2 绕，否则就保持原来的路径。
此时 $dis_3=min(114514,1+1)=2$，更新成功。
这个操作我们下面称为 $relax(2,3)$，$relax$ 也就是平时说的“松弛”。
$relax(u,v)$ 定义为 $dis_v=min(dis_v,dis_u+w(u,v))$。
显然 $relax(u,v)$ 的目的是用 $u,v$ 之间的边权更新 $dis_v$。
这个式子应该是所有最短路算法的核心。
后面的算法都可以去这里看代码。
Bellman-Ford
非常好理解，把每个边都 $relax\ n-1$ 遍。
那为什么是 $n-1$ 遍呢？其实我也不太懂
在最短路存在的情况下，由于一次松弛操作会使最短路的边数至少 $+1$，而最短路的边数最多为 $n-1$，因此整个算法最多执行 $n-1$ 轮松弛操作。
OIwiki上是这么说的。理解不了没关系，后面也用不到。
显而易见 $O(nm)$ 复杂度，所以一般的题都是过不去的。
SPFA
Shortest Path Faster Algorithm。
因为在 $relax(u,v)$ 后，下一次操作只可能是 $relax(v,$某个点$)$。
所以我们只需要按照 $bfs$ 遍历图（不限制一个点多次遍历），每次 $relax($遍历到的点，这个点的出点$)$ 即可。
实际上只是减少了上面那个算法的 $relax$ 次数，最坏情况下和上面一样 $O(nm)$。
所以没负权别用 SPFA。复杂度 $O(nk)$（$k=$玄学）。
当然 SPFA 有个优化叫 SLF：
将普通队列换成双端队列，每次将入队结点距离和队首比较，如果更大则插入至队尾，否则插入队首。
这种优化相对不容易被卡，可以带上。
Dijkstra
最实用的单源最短路。
仍然是 bfs，但过程有所改变：
-
将队列换成优先队列（小根堆），每次将 $v$ 入队时也将 $dis_v$ 入队，按 $dis_v$ 排序小根堆。
-
限制一个点多次入队，也就是遍历到 $v$ 后 $dis_v$ 确定为最优。
那么有同学就有疑问了：为什么每次遍历到 $v$ 后 $dis_v$ 就能确定为最优呢？
我们先假设所有 $dis_i$ 被确定为最优的 $i$ 在集合 $A$ 中，其他点在 $B$ 中。
当然，一开始 $A$ 中只有一个 $s$ 点。
那么，当前优先队列的队头 $v$ 就是 $A$ 中所有点的最小出边连的点，且在 $B$ 中。
所以我们可以确定，$v$ 的前驱点 $u$ 一定在 $A$ 中
既然 $A$ 中的点已经确定最短路，那么 $v$ 的最短路肯定要把这个与 $u$ 的相连的最短路走一遍。
那么再下一步，肯定要走这个最小出边，否则从别的点绕一定更远。
那如果有负权，就不一定了。
如果有负权，那从别的点绕可能可以再走一个负权边回来，比走最小出边更好。
所以 Dijkstra 不能跑负权。
言归正传， Dijkstra 的过程就是：
- 找到 $A$ 中所有点的最小出边连的点（原在 $B$ 中），加入 $A$ 中。
- $relax$ 这个点的所有出边。
当然，原来的 Dijkstra 是暴力找最小出边连的点，这里用堆优化。
如果你看不懂正确性证明也没关系，毕竟贪心不需要证明
全源最短路
Floyd
有人不会吗？
dp[i][j] 表示 $i$ 到 $j$ 最短路长度，
则有转移方程 dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])(1≤k≤n)
