1.20 模拟赛口胡题解
幸亏 DP 都在前面签到，否则我又得寄
A
签到题。来点 $O(n^2)$ 正解。
$\forall k$ 做线段集为 $\{[l,r]|\sum\limits_{i=l}^ra_i=k\}$ 的线段覆盖的结果最大值。
具体地，按 $r$ 正序枚举 $[l,r]$，考虑把 $[l,r]$ 加入 $k=\sum\limits_{i=l}^ra_i$ 的贡献。
#include <cstdio>
#include <algorithm>
using namespace std;
int n, q, a[1050], R[10000050], C[10000050];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d", a + i), a[i] += a[i - 1];
for (int r = 1; r <= n; ++r)
for (int l = r, v; l; --l)
if (R[v = a[r] - a[l - 1]] < l)
R[v] = r, q = max(q, ++C[v]);
return !printf("%d", q);
}（$R_v$ 为 $k=v$ 的子问题当前最右端点，$C_v$ 为 $k=v$ 的子问题结果）
当然你谷神机已经无压力 1s 1e9 了，所以写个 $O(n^3)$ 大概率也是能过的（快进到 1e3 成为 $O(n^3)$ 共识
B
概率 DP 板子。
逆推：设 $f_i$ 为从 $i$ 到 $n$ 的期望，则有
$$ f_i=\dfrac{\sum\limits_{j=i+1}^{\min(i+6,n)}f_j}{\min(6,n-i)}+a_i $$
正推：设 $f_i$ 为从 $1$ 到 $i$ （不一定经过 $i$）的期望，则有
$$ f_i=\sum\limits_{j=\max(i-6,1)}^{i-1}\dfrac{f_j+a_ig_j}{\min(6,n-j)} $$
其中 $g_i$ 为到达 $i$ 的概率，且有
$$ g_i=\sum\limits_{j=\max(i-6,1)}^{i-1}\dfrac{g_j}{\min(6,n-j)} $$
觉得一堆 $\min\max$ 很烦可以把 DAG 建出来。
逆推：
#include <cstdio>
#include <algorithm>
using namespace std;
int n, a[1050];
double f[1050];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d", a + i);
f[n] = a[n];
for (int i = n - 1; i; --i)
{
for (int j = 1; j <= min(6, n - i); ++j)
f[i] += f[i + j];
f[i] = f[i] / min(6, n - i) + a[i];
}
printf("%.7lf", f[1]);
return 0;
}正推：
#include <cstdio>
#include <algorithm>
using namespace std;
int n, a[1050];
double f[1050], g[1050];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d", a + i);
f[1] = a[1];
g[1] = 1;
for (int i = 2; i <= n; ++i)
for (int j = 1; j <= min(6, i - 1); ++j)
f[i] += (f[i - j] + a[i] * g[i - j]) / min(n - i + j, 6), g[i] += g[i - j] / min(n - i + j, 6);
printf("%.7lf", f[n]);
return 0;
}C
树形 DP 板子。
设 $f_i$ 为 $i$ 子树内权值和最大的子树的权值和，则有
$$ f_u=\max\{s_u,f_v|v\in\text{son}_u\} $$
其中 $s_i$ 为 $i$ 子树权值和，且有
$$ s_u=a_u+\sum\limits_{v\in\text{son}_u}s_v $$
DP 过程中更新答案。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
struct E
{
int v, t;
} e[200050];
int n, c, q = -2e9, s[100050], f[100050], h[100050];
void A(int u, int v)
{
e[++c] = {v, h[u]};
h[u] = c;
}
void D(int u, int k)
{
for (int i = h[u], v; i; i = e[i].t)
if ((v = e[i].v) != k)
D(v, u), s[u] += s[v], q = max(q, f[u] + f[v]), f[u] = max(f[u], f[v]);
f[u] = max(f[u], s[u]);
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d", s + i);
for (int i = 1, u, v; i < n; ++i)
scanf("%d%d", &u, &v), A(u, v), A(v, u);
memset(f, 0xc0, sizeof f);
D(1, 0);
if (q < -1e9)
puts("Impossible");
else
printf("%d", q);
return 0;
}D
猜结论。
结论：DAG 加若干条不定向的边一定能组成 DAG。
总的反转代价是由所有需要反转的边中，代价最高的那一条决定的，求达成目标的最小代价。
最大值最小，二分。
二分代价 $k$，则边权 $\le k$ 的边可以任意反转，若边权 $>k$ 的边组成 DAG，则此 DAG 加入边权 $\le k$ 的不定向边一定能组成 DAG，则此代价 $k$ 合法。
#include <queue>
#include <cstdio>
#include <cstring>
using namespace std;
struct S
{
int u, v, w;
} s[100050];
struct E
{
int v, t;
} e[100050];
queue<int> q;
int n, m, c, L, R = 1e9, M, d[100050], h[100050];
void A(int u, int v)
{
++d[v];
e[++c] = {v, h[u]};
h[u] = c;
}
bool C(int k)
{
int r = 0;
memset(e, 0, sizeof e);
memset(d, 0, sizeof d);
memset(h, c = 0, sizeof h);
for (int i = 0; i < m; ++i)
if (s[i].w > k)
A(s[i].u, s[i].v);
for (int i = 1; i <= n; ++i)
if (!d[i])
q.push(i);
while (!q.empty())
{
int u = q.front();
q.pop();
++r;
for (int i = h[u], v; i; i = e[i].t)
if (!--d[v = e[i].v])
q.push(v);
}
return r == n;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < m; ++i)
scanf("%d%d%d", &s[i].u, &s[i].v, &s[i].w);
while (L <= R)
if (C(M = L + R >> 1))
R = M - 1;
else
L = M + 1;
printf("%d", L);
return 0;
}E
DS。
赛时看到换根想 LCT，然后发现 LCT 不好维护子树信息，现学 ETT 换根失败，Top Tree 又不会写（
当然拿上面提到的动态树都是可以嗯做这题的，考虑容易的做法。
找规律。（在拿 DFS 序嗯造 ETT 的时候找到的，不知道 zq 什么做法）
考虑线段树维护 DFS 序，发现只有换根操作不好维护。
分类讨论查询 $x$ 时 $1,x,\text{root}$ 的位置关系。
- $x=\text{root}$：全局最小值。
- $x$ 不在 $1\to\text{root}$ 路径上：以 $1$ 为根意义下 $x$ 子树最小值。
- $x$ 在 $1\to\text{root}$ 路径上：设 $Z$ 为 $\text{root}$ 的 $\text{dep}_{\text{root}}-\text{dep}_x-1$ 级祖先的子树，答案为 $\complement_UZ$ 的最小值。
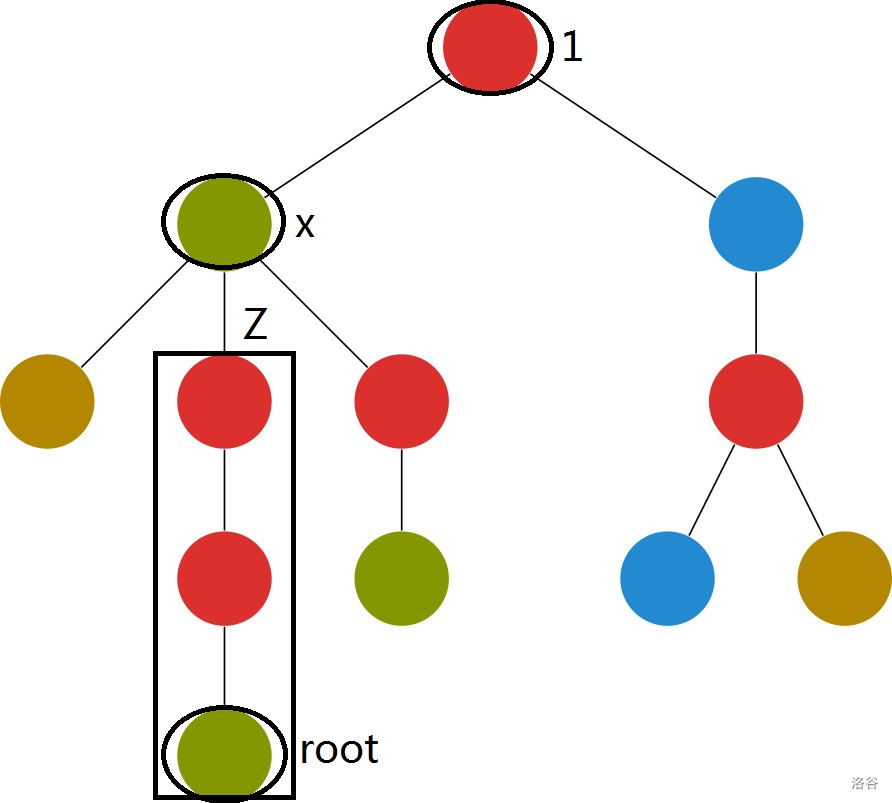
（辅助理解第三种情况）
树上倍增维护 $k$ 级祖先，你要写长剖我不拦你。
#include <cstdio>
#include <algorithm>
#define G int m = p->s + p->t >> 1
using namespace std;
struct E
{
int v, t;
} e[200050];
int n, m, c, g, R, a[100050], b[100050], k[100050], d[100050], s[100050], h[100050], f[100050][20];
char o;
void A(int u, int v)
{
e[++c] = {v, h[u]};
h[u] = c;
}
void D(int u)
{
s[k[b[u] = ++g] = u] = 1;
for (int i = h[u], v; i; i = e[i].t)
if (!d[v = e[i].v])
{
d[v] = d[u] + 1;
f[v][0] = u;
for (int j = 1; f[v][j - 1]; ++j)
f[v][j] = f[f[v][j - 1]][j - 1];
D(v);
s[u] += s[v];
}
}
struct T
{
T *l, *r;
int s, t, v;
T(int s, int t) : s(s), t(t) {}
void u() { v = min(l->v, r->v); }
} * r;
void B(int s, int t, T *&p)
{
p = new T(s, t);
if (s == t)
return void(p->v = a[k[s]]);
G;
B(s, m, p->l);
B(m + 1, t, p->r);
p->u();
}
void M(int l, int k, T *p)
{
if (p->s == p->t)
return void(p->v = k);
G;
if (l <= m)
M(l, k, p->l);
else
M(l, k, p->r);
p->u();
}
int Q(int l, int r, T *p)
{
if (l <= p->s && p->t <= r)
return p->v;
G;
int q = 1e9;
if (l <= m)
q = min(q, Q(l, r, p->l));
if (r > m)
q = min(q, Q(l, r, p->r));
return q;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = R = 1, x; i <= n; ++i)
{
scanf("%d%d", &x, a + i);
if (x)
A(x, i), A(i, x);
}
D(d[1] = 1);
B(1, n, r);
for (int i = 0, x, y, z, q; i < m; ++i)
{
scanf(" %c%d", &o, &x);
switch (o)
{
case 'V':
scanf("%d", &y);
M(b[x], y, r);
break;
case 'E':
R = x;
break;
case 'Q':
if (x == R)
printf("%d\n", r->v);
else
{
z = R;
for (int k = 0; k <= 30; ++k)
if (d[R] - d[x] - 1 & 1 << k)
z = f[z][k];
if (f[z][0] != x)
printf("%d\n", Q(b[x], b[x] + s[x] - 1, r));
else
{
q = Q(1, b[z] - 1, r);
if (b[z] + s[z] <= n)
q = min(q, Q(b[z] + s[z], n, r));
printf("%d\n", q);
}
}
}
}
return 0;
}F
不会。
