NOIP 第二次

A

观察发现排序后一定选一个前缀，所以双指针维护一下即可。

B

从前往后依次标边权。

• 这条边是蓝的：直接把没用过的最小权值给这条边。
• 这条边是白的：这条边 $(u,v)$ 需要比最小生成树上 $u\to v$ 的边都大，
  所以先把最小生成树上 $u\to v$ 中没标边权的边按出现顺序依次标上当前没用过的最小权值，
  然后把此时没用过的最小权值给 $(u,v)$ 这条边即可。

C

设 $f_i$ 表示只考虑 $[1,i]$ 中的线段，能保留的最大权值和。

对 $f_i$ 考虑其到 $f_j|j>i$ 的转移，可以发现有 $f_j\gets\max\{f_j,f_i+k(S)\}$，

其中 $S$ 表示 $(i,j]$ 中的线段集，也就是可以入选 $f_j$ 比 $f_i$ 多出的一个连通块的线段集，

$k(S)$ 表示 $S$ 的前 $k$ 大权值和，也就是 $f_j$ 比 $f_i$ 多出的一个连通块的最大权值和。

把线段按右端点排序，用堆维护 $S$ 即可维护这个转移。

D

先把矩形加，单点查询差分成单点加，矩形查询。

然后可以发现平移一个矩形相当于加入四条线段，那么现在是线段加，矩形查询。

水平、竖直的线段的贡献可以直接扫描线，考虑斜着的。

斜率为 $-1$

按 $x+y$ 扫描线，可以发现处理 $(x,y)$ 处的询问时，答案为当前扫过的线段的贡献之和减去下图中红框部分的贡献之和。

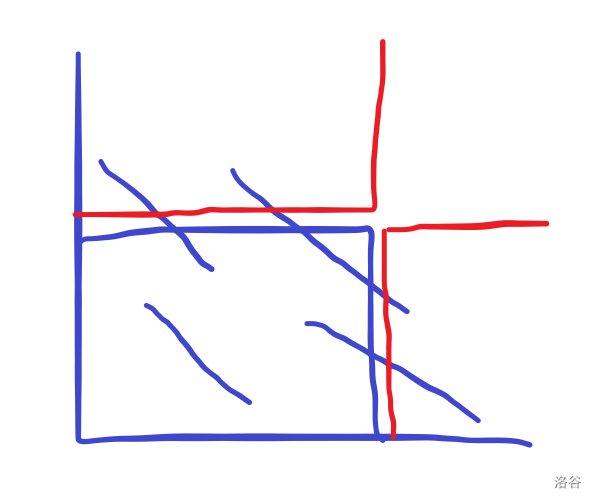
开两个线段树，$c_i$ 维护当前扫过的线段对 $x=i$ 上的点的贡献，$d_i$ 维护当前扫过的线段对 $y=i$ 上的点的贡献，

于是分别查询 $c,d$ 的区间和即可得到红框部分的贡献之和。

斜率为 $1$

按 $x-y$ 扫两次，

一次对所有询问统计下图中红线上方（线段的 $x-y$ 小于等于询问的 $x-y$）的贡献，

一次对所有询问统计下图中红线下方（线段的 $x-y$ 大于询问的 $x-y$）的贡献。

同样地，第一次扫描维护 $d$，第二次扫描维护 $c$，分别查区间和即可得到相应的贡献。