P5538 【XR-3】Namid[A]me 题解
对原树任意剖一下，然后链数等于叶子数。考虑分别算 $i,j$ 在相同 / 不同链上的贡献。
注意到一个点 $i$ 向链顶 / 链底延伸，形成的树链的 $f$ 值都不超过 $O(\log V)$ 种，
记下这些 $f$ 值的位置，记这些树链为 $i$ 的前缀 / 后缀。
考虑 $i,j$ 在相同链上的贡献，对每个 $i$ 统计其所有后缀即可。
考虑 $i,j$ 在不同链上的贡献，枚举这两条链，分情况讨论：
链顶无祖先关系
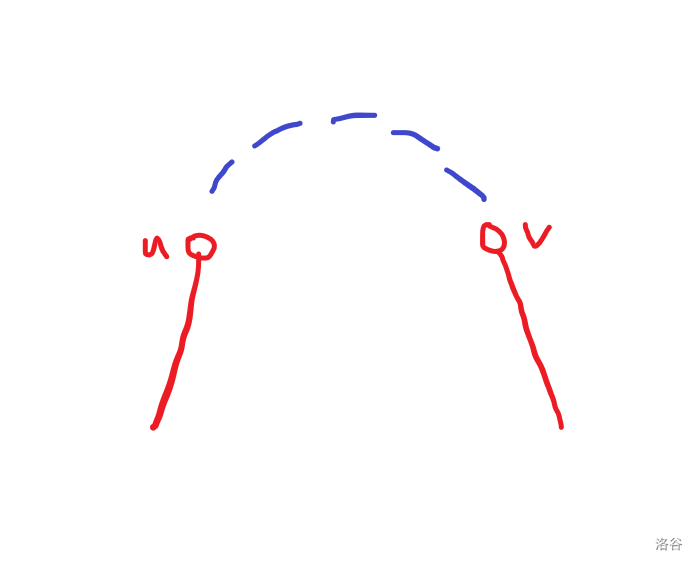
如图，$i\to j$ 的链一定由 $u$ 的一段后缀，$u\to v$，$v$ 的一段后缀拼成，
分别枚举 $u$ 的这段后缀、$v$ 的这段后缀取到哪个 $f$ 值即可。
链顶有祖先关系
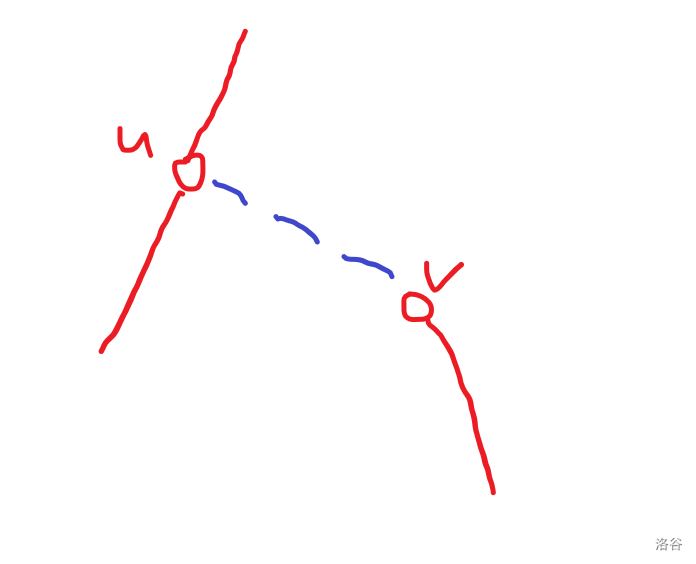
如图，$i\to j$ 的链一定由 $u$ 的一段前缀 / 后缀，$u\to v$，$v$ 的一段后缀拼成，
分别枚举 $u$ 的这段前缀 / 后缀，$v$ 的这段后缀取到哪个 $f$ 值即可。
复杂度 $O(d^2\log^2V)$，可以利用原根做到 $O(1)$ 光速幂。
%:include <cstdio>
%:include <vector>
%:include <algorithm>
%:define M 786433
using namespace std;
inline int R()
{
int q = 0;
char c = getchar();
while (c < '0' || c > '9')
c = getchar();
while (c >= '0' && c <= '9')
q = q * 10 + c - '0', c = getchar();
return q;
}
struct E
{
int v, t;
} e[400050];
pair<int, int> S0[400050][32], S1[400050][32];
int n, c, p, q, lg[M], _g[M], l0[50], l1[50], j0[400050], j1[400050], a[400050], z[400050], d[400050], f[400050], s[400050], t[400050], b[400050], h[400050], F[400050][20];
long long P(int x, int y) { return x % M ? _g[1ll * y * lg[x % M] % (M - 1)] : 0; }
void A(int u, int v)
{
e[++c] = {v, h[u]};
h[u] = c;
}
void X(int u, int k)
{
s[u] = 1;
for (int i = h[u], v; i; i = e[i].t)
if ((v = e[i].v) != k)
{
d[v] = d[f[v] = u] + 1;
X(v, u);
s[u] += s[v];
if (s[v] > s[z[u]])
z[u] = v;
}
}
void Y(int u, int k)
{
b[u] = ++p;
t[u] = k;
if (z[u])
Y(z[u], k);
for (int i = h[u], v; i; i = e[i].t)
if ((v = e[i].v) != f[u] && v != z[u])
Y(v, v);
}
int _F(int x, int y)
{
int k = __lg(y - x + 1);
return F[x][k] & F[y - (1 << k) + 1][k];
}
int QF(int x, int y)
{
int q = ~0;
while (t[x] != t[y])
{
if (d[t[x]] < d[t[y]])
swap(x, y);
q &= _F(b[t[x]], b[x]);
x = f[t[x]];
}
if (d[x] > d[y])
swap(x, y);
return q & _F(b[x], b[y]);
}
int T(int x, int y)
{
while (t[x] != y)
x = f[t[x]];
return x;
}
void Q(int F, int Z, int y)
{
if (!Z)
return;
int f = F;
q = (q + P(f, f) * Z * S1[y][0].first) % M;
for (int k = 0; k < 30; ++k)
{
if (a[y] >> S1[y][k].second & 1)
f &= ~(1ll << S1[y][k].second);
q = (q + P(f, f) * Z * (S1[y][k + 1].first - S1[y][k].first)) % M;
}
if (a[y] >> S1[y][30].second & 1)
f &= ~(1ll << S1[y][30].second);
q = (q + P(f, f) * Z * (j1[y] - S1[y][30].first)) % M;
}
signed main()
{
_g[0] = 1;
for (int i = 1; i < M; ++i)
lg[_g[i] = _g[i - 1] * 10 % M] = i;
n = R();
for (int i = 1; i <= n; ++i)
a[i] = R();
for (int i = 1, u, v; i < n; ++i)
u = R(), v = R(), A(u, v), A(v, u);
X(1, 0);
Y(1, 1);
for (int i = 1; i <= n; ++i)
F[b[i]][0] = a[i];
for (int j = 1; 1 << j <= n; ++j)
for (int i = 1; i + (1 << j) - 1 <= n; ++i)
F[i][j] = F[i][j - 1] & F[i + (1 << j - 1)][j - 1];
for (int i = 1; i <= n; ++i)
if (!z[i])
{
for (int j = 0; j <= 30; ++j)
l0[j] = l1[j] = 0;
for (int j = 1, x = i;; x = f[x], ++j)
{
j1[x] = j;
for (int k = 0; k <= 30; ++k)
if (a[x] >> k & 1)
l1[k] = j, S1[x][k] = {j - l0[k], k};
else
l0[k] = j, S1[x][k] = {j - l1[k], k};
sort(S1[x], S1[x] + 31);
int f = a[x];
q = (q + P(f, f) * S1[x][0].first) % M;
for (int k = 0; k < 30; ++k)
{
if (a[x] >> S1[x][k].second & 1)
f &= ~(1ll << S1[x][k].second);
q = (q + P(f, f) * (S1[x][k + 1].first - S1[x][k].first)) % M;
}
if (a[x] >> S1[x][30].second & 1)
f &= ~(1ll << S1[x][30].second);
q = (q + P(f, f) * (j - S1[x][30].first)) % M;
if (x == t[x])
break;
}
}
for (int i = 1; i <= n; ++i)
if (i == t[i])
{
for (int j = 0; j <= 30; ++j)
l0[j] = l1[j] = 0;
for (int j = 1, x = i;; x = z[x], ++j)
{
j0[x] = j;
for (int k = 0; k <= 30; ++k)
if (a[x] >> k & 1)
l1[k] = j, S0[x][k] = {j - l0[k], k};
else
l0[k] = j, S0[x][k] = {j - l1[k], k};
sort(S0[x], S0[x] + 31);
if (!z[x])
break;
}
}
for (int i = 1; i <= n; ++i)
if (!z[i])
for (int j = i + 1; j <= n; ++j)
if (!z[j])
{
int x = t[i], y = t[j];
if (d[x] > d[y])
swap(x, y);
if (b[x] <= b[y] && b[y] < b[x] + s[x])
x = T(y, x);
int F = QF(x, y), T = F;
Q(F, S1[x][0].first, y);
for (int k = 0; k < 30; ++k)
{
if (a[x] >> S1[x][k].second & 1)
F &= ~(1ll << S1[x][k].second);
Q(F, S1[x][k + 1].first - S1[x][k].first, y);
}
if (a[x] >> S1[x][30].second & 1)
F &= ~(1ll << S1[x][30].second);
Q(F, j1[x] - S1[x][30].first, y);
F = T;
Q(F, S0[x][0].first - 1, y);
for (int k = 0; k < 30; ++k)
{
if (a[x] >> S0[x][k].second & 1)
F &= ~(1ll << S0[x][k].second);
Q(F, S0[x][k + 1].first - S0[x][k].first, y);
}
if (a[x] >> S0[x][30].second & 1)
F &= ~(1ll << S0[x][30].second);
Q(F, j0[x] - S0[x][30].first, y);
}
printf("%d", q);
return 0;
}