周（指三天）测题解9.9
个人认为最难的一次。
T1
只需要注意：
最好把除了 $k$ 的变量开 double。
其他正常带式子即可。
T2
这里介绍一个 STL 函数：find_first_of。
如果 s，t 是 string 类型的，那么就可以用 s.find_first_of(t)
来得到 s 中第一个被 t 包含的字符的位置。
是不是很蒙？我们看 C++Refrence 上的一个例程：
// string::find_first_of
#include <iostream>
#include <string>
int main ()
{
std::string str ("PLease, replace the vowels in this sentence by asterisks.");
std::string::size_type found = str.find_first_of("aeiou");
while (found!=std::string::npos)
{
str[found]='*';
found=str.find_first_of("aeiou",found+1);
}
std::cout << str << '\n';
return 0;
}我们为了理解，可以给参数 t 中的所有字符取一个统称。
比如在这个例程里，t = "aeiou"，我们叫它“元音”。
那么 str.find_first_of("aeiou") 的作用就是找 str 中的第一个元音。
所以这个例程的作用就是把所有元音换成 *。
恍然大悟否？
而且，t 后面可以跟一个下标位置参数，表示从这个位置开始往后找。
接下来让我们看题。
对于每一组易混淆字符，我们都在原字符串里 find_first_of。
即找原字符串中第一个易混淆字符，然后再继续找第二个，第三个……直到找不到为止。
每找到一个易混淆字符，ans 就 *= 易混淆字符的数量。
记得开 ll 和取模。
#include <iostream>
#include <string>
using namespace std;
string s, t;int n;long long ans = 1;
int main()
{
cin >> s >> n;
for(int i = 0;i < n;++i)
{
cin >> t;
int st = s.find_first_of(t);
while(st != -1)
{
ans *= t.length(), ans %= 1000000007;
st = s.find_first_of(t, st + 1);
}
}
cout << ans;
return 0;
}T3
基环树。虽然我不会
其实只是一个 dfs 实现的，带个特判的拓扑罢了。‘
样例太蒻了，我们来自己造个样例：
7
6 1 1 2 2 3 3下文出现的所有字母和表达式指的都是在 $a$ 中的下标。
基环树是啥
首先定义：如果选了 $i$ 就不能选 $j$，则称为 $i$ 排斥 $j$。
也就是对于所有 $i$，$i$ 排斥 $a[i]$。
我们可以想到，若 $i$ 排斥 $j$，则 $i$ 到 $j$ 连边。
那么最后可以连出一个图，其中每个结点都只有一条出边。
那我们造的样例就是这样：
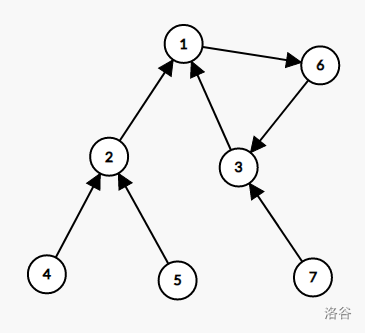
而且图中可能有环，但环之间不连通。
那么这个东西就可以定义为：
有若干个不连通的环，环上每个点都带着一个树。
这玩意就是个基环树森林。
贪心思路
首先我们要知道，排斥是双向的。
即如果 $a[i]=j$，那选了 $i$ 就选不了 $j$，选了 $j$ 就选不了 $i$。
理解起来会有点费劲。我们拿题里的样例 3 1 3 解释一下：
因为 $a[1]=3$，所以选了第 $1$ 项就不能选第 $3$ 项。
而且，选了第 $3$ 项也不能再选第 $1$ 项。（只考虑 $a[1]=3$ 这一个排斥关系。）
但为了好理解，还是用单向边表示树形结构更清晰一点。
我们知道，每个点都排斥自己的父亲。
所以选了一个点后，就不能选它的父亲。
而且因为上面的双向排斥，每个点都排斥自己的所有孩子。
所以选了一个点后，就不能选它的任意一个孩子。
我们就可以简单的想到两种贪心：
- 从每个根开始往下搜，往下能选就选。
- 从每个叶子开始往上搜，往上能选就选。
思路 1 其实就是隔一层选一层，显然是不对的。
能选就选怎么实现呢？
可以记录每个点的入度，在搜到一个点后将它的父节点入度减减。
如果一个点决定不选，或者入度为 0，就可以往上搜。
那么我们可以轻松写出第二种的代码：
#include <iostream>
using namespace std;
int a[300050], in[300050], n, ans;bool vis[300050];
void dfs(int x, bool chs)
{
if(vis[x]) return;
vis[x] = 1;--in[a[x]];
if(chs) ++ans;
if(!in[a[x]]) dfs(a[x], !chs);
else if(chs) dfs(a[x], 0);
}
int main()
{
cin >> n;
for(int i = 1;i <= n;++i)
cin >> a[i], ++in[a[i]];
for(int i = 1;i <= n;++i)
if(!in[i]) dfs(i, 1);
cout << ans;
return 0;
}之后，你就会获得 70 分的好成绩。
为什么呢？我们考虑一个输入：
3
2 3 1很明显是选任意一个。
但你会发现，这个数据里没有叶子节点。
但处理起来也很简单：
直接无视环，把第一遍没搜到的以不选的状态开始搜。
#include <iostream>
using namespace std;
int a[300050], in[300050], n, ans;bool vis[300050];
void dfs(int x, bool chs)
{
if(vis[x]) return;
vis[x] = 1;--in[a[x]];
if(chs) ++ans;
if(!in[a[x]]) dfs(a[x], !chs);
else if(chs) dfs(a[x], 0);
}
int main()
{
cin >> n;
for(int i = 1;i <= n;++i)
cin >> a[i], ++in[a[i]];
for(int i = 1;i <= n;++i)
if(!in[i]) dfs(i, 1);
for(int i = 1;i <= n;++i)
if(!vis[i]) dfs(i, 0);
cout << ans;
return 0;
}这题就切了。其实我觉得这题可能有个蓝题难度。
T4
一个简单的冰法师，但细节有亿点点多。
- 不一定是简单路径，意味着如果有两个相邻相同点就是-1。
- 搜索时要对每个点先扩展一次来确定公比。
- 等比数列里不能有0！等比数列里不能有0！等比数列里不能有0！
然后程序就出来了：
#include <iostream>
#include <vector>
#include <queue>
#include <cstdlib>
using namespace std;
struct st
{
int x, y, q, dep;
st(int _x, int _y, int _q, int _dep)
{
x = _x, y = _y, q = _q, dep = _dep;
}
};
vector<int> a[40050];vector<bool> vis[40050];int n, m, ans = 1, f[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
bool ok(int x, int y) {return x >= 0 && x < n && y >= 0 && y < m;}
void bfs(int x, int y)
{
queue<st> q;
for(int i = 0;i < 4;++i)
{
int vx = x + f[i][0], vy = y + f[i][1];
if(!ok(vx, vy)) continue;
if(a[vx][vy] == a[x][y]) cout << -1, exit(0);
if(a[vx][vy] && a[vx][vy] % a[x][y] == 0)
q.push(st(vx, vy, a[vx][vy] / a[x][y], 2));
}
while(!q.empty())
{
st s = q.front();q.pop();
if(vis[s.x][s.y] && s.dep < ans) continue;
vis[s.x][s.y] = 1;
for(int i = 0;i < 4;++i)
{
int vx = s.x + f[i][0], vy = s.y + f[i][1];
if(!ok(vx, vy)) continue;
if(a[s.x][s.y] * s.q == a[vx][vy])
q.push(st(vx, vy, s.q, s.dep + 1));
}
ans = max(ans, s.dep);
}
}
int main()
{
cin >> n >> m;
for(int i = 0;i < n;++i)
for(int j = 0, t;j < m;++j)
{
cin >> t;
a[i].push_back(t);
vis[i].push_back(0);
}
for(int i = 0;i < n;++i)
for(int j = 0;j < m;++j)
{
if(!a[i][j]) continue;
if(!vis[i][j]) bfs(i, j);
}
cout << ans;
return 0;
}接下来，还剩最后一步：
把鼠标停在右下角的加号上，点一下上面的第一个图标。
祝大家下次模拟赛RP++
