T3のO(1)做法

RT

---

先看图

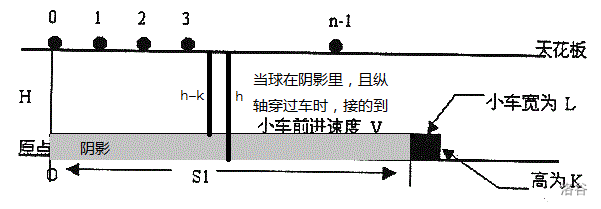
看明白这张图，就明白一半了，接下来开始推柿子。

我们还知道，$d=0.5gt^2$，$d$是小球落下的距离。

$g=10$，那么$d=5t^2$，那么$\dfrac d5=t^2$，那么$\sqrt{\dfrac d5}=t$。

如果要接到球，上图中$d$的范围就是$h-k≤d≤h$了（两条黑线）。

那么$\dfrac{h-k}5≤\dfrac d5≤\dfrac h5$，那么$\sqrt{\dfrac{h-k}5}≤\sqrt{\dfrac d5}≤\sqrt{\dfrac h5}$。

所以如果在$x$的时间能接到球，那么$\sqrt{\dfrac{h-k}5}≤x≤\sqrt{\dfrac h5}$。

接下来，就要算出小车在这段时间内覆盖到的长度了。

为了方便，接下来 $maxt=\sqrt{\dfrac h5},mint=\sqrt{\dfrac{h-k}5}$

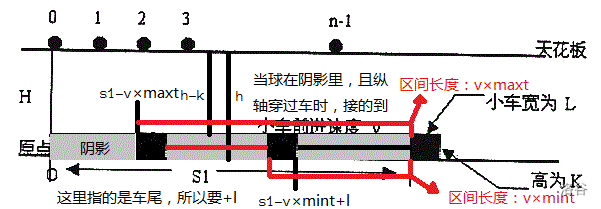
这里可以看出区间为$s1-v×maxt$到$s1-v×mint+l$，下文记为$begin$到$end$。

但如果直接相减，你会发现连样例都过不去。

因为左右端点可能超过$[0,n]$的范围，即接了不存在的球。

所以$begin=max(begin,0),end=min(end,n)$。

现在相减就可以啦~

#include <iostream>
#include <cmath>
using namespace std;
double h, s, v, l, k, n;
int main()
{
    cin >> h >> s >> v >> l >> k >> n;
    double maxt = sqrt(h / 5), mint = sqrt((h - k) / 5);
    int begin = s - v * maxt, end = s - v * mint + l;
    if(begin < 0) begin = 0;
    if(end > n) end = n;
    cout << end - begin;
    return 0;
}