10.3题解

考场脑抽T2读错题了

T1

签到题。

模拟大家都会，下面是 $O(1)$ 做法：

#include <iostream>
using namespace std;
int w, k, a, n;
int main()
{
    cin >> w >> k >> a >> n;
    if(n > k)
        cout << (2 * n * w + a * k * (2 * n - k - 1)) / 2;
    else
        cout << n * (2 * w + a * (n - 1)) / 2;
    return 0;
}

T2

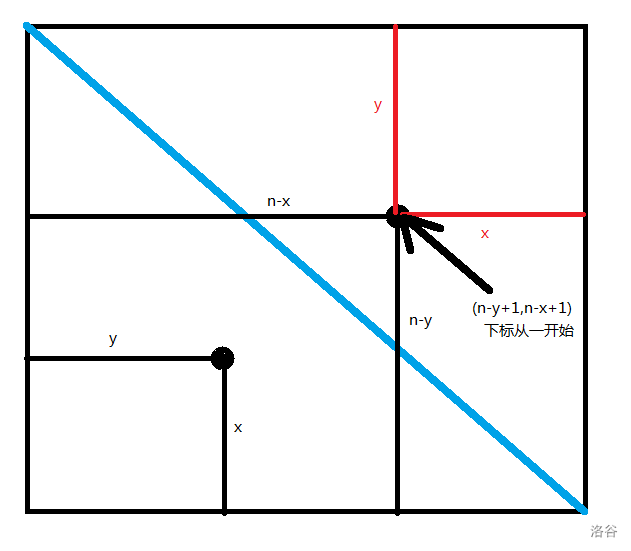
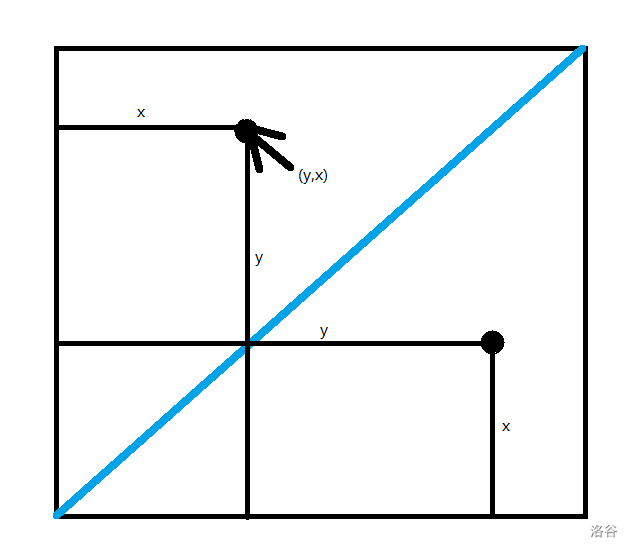
下图中特别大的两个点是对称点，没有箭头的点坐标为 (x,y)。

主对角线：

副对角线：

注意判断点是否喵喵点时，既要判断本身，又要判断对称点！

如果某个位置是 1 ，并且它关于主对角线对称的位置和关于副对角线对称的位置都为 1 ，那么这个点就称为一个喵喵点。

#include <iostream>
#include <cstdio>
using namespace std;
int n, a[150][150], ans, vx, vy;
int main()
{
    cin >> n;
    for(int i = 1;i <= n;++i)
        for(int j = 1;j <= n;++j)
            scanf("%1d", &a[i][j]);
    for(int i = 1;i <= n;++i)
        for(int j = 1;j <= n;++j)
            if(a[i][j] && a[j][i] && a[n - j + 1][n - i + 1]) ++ans;
    cout << ans;
    return 0;
}

T3

我们要知道，选出的两个数排序后一定相邻。

---

首先，$(a\wedge b)\oplus (a\vee b)$ 与 $a\oplus b$ 是等价的。

因为 $a\wedge b$ 算的是 $a,b$ 二进制中的交，

$a\vee b$ 算的是 $a,b$ 二进制中的并，

而且并一定是包含交的，

而交和并的不同部分，就是在并中但不在交中的部分，

换句话说，就是 $a,b$ 中的不同部分，也就是 $a\oplus b$。

那么题意就可以转化为：

给定数列 $a$，选出两个数 $a_x,a_y$，使得 $a_x\oplus a_y$ 最小。

---

那么为什么选出的两个数排序后一定相邻呢？

我们知道，想要两个数异或值最小，那么这两个数要尽量接近。

那么我们假如选了排序后不相邻的 $a_x,a_y$，

则排序后的 $a_{x+1}\oplus a_y$ 和 $a_x\oplus a_{y-1}$ 一定有一个 $<$ $a_x\oplus a_y$。

所以只需要拍一遍序，枚举相邻的两个数，每次更新答案即可。

#include <iostream>
#include <algorithm>
using namespace std;
int n, a[100050], ans = 1e9;
int main()
{
    cin >> n;
    for(int i = 0;i < n;++i)
        cin >> a[i];
    sort(a, a + n);
    for(int i = 1;i < n;++i)
        ans = min(ans, a[i] ^ a[i - 1]);
    cout << ans;
    return 0;
}

T4

$ToBeContinue$