析合树学习笔记
析合树是一种连续段数据结构。
引入:
给定排列
,求值域连续的段的个数。
概念
排列 是排列。
连续段 是值域连续的段,满足集合运算。
值域区间 是连续段值域的区间。
本原段 是不与其他连续段部分相交的连续段。
连续段集
形式化地,
定义序列
定义
连续段
定义
定义连续段集
定义连续段
定义本原段集
析点与合点
析合树的点集是
概念
节点
节点
节点
节点
节点
形式化地,
定义节点
定义节点
注意,
定义节点
定义节点
定义节点
性质
证明:若命题不成立,则
形式化地,
建树
可以用 增量法
将
策略
维护当前
- 重复上述方案直到不能进行(即找不到 2. 中合法的

(来自 CF,对
根据上述策略,我们需要快速判断
子问题
考虑如何快速判断
维护
考虑更新
在
设
用单调栈维护后缀最值的位置,以后缀最小值为例。
维护单调递增的栈
后缀最大值同理。
转化为区间加,单点查询,找最左
例题
P8600 [蓝桥杯 2013 省 B] 连号区间数 / CF526F Pudding Monsters
给定排列
,求值域连续的段的个数。
考虑析合树内每个点的贡献。
由合点的性质,若
由析点的性质,若
注意到
代码:指针 1.98KB 199ms 8.48MB,非指针 2.02KB 207ms 9.66MB
一些序列上连续段问题可以转化为析合树上问题。
P4747 [CERC2017]Intrinsic Interval
给定排列
, 次询问包含某区间的最短连续段。
只讨论在线做法。
考虑对询问区间
由合点的性质,若
由析点的性质,若
没了的 JDOI GLAOI R1 没了的 T4LAOI 没了的入团赛 T4无中生题给定排列
, 次询问包含某区间的连续段数量。
这题比较饱经风霜,所以题解比较详细(
考虑对询问区间
容易发现只有
考虑
若
(
维护树上前缀和数组
令
若
若
不难得到递推式:
两部分贡献加起来即可。
众所周知析合树的题都可以不用析合树做,所以如果有人会不用析合树做这个可以私我(
给定排列
, 次询问某区间包含的连续段数量。
只讨论在线做法。
相当于区间 CF526F,所以考虑类似想法。
定义析合树内每个点的贡献:
由合点的性质,若
是合点,则 的任意子段构成连续段,即 的贡献为 。 由析点的性质,若
是析点,则 的任意多元素子段不构成连续段,即 的贡献为 。
定义
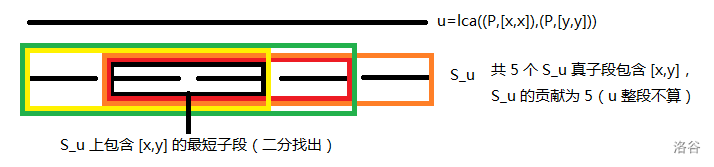
考虑询问
设
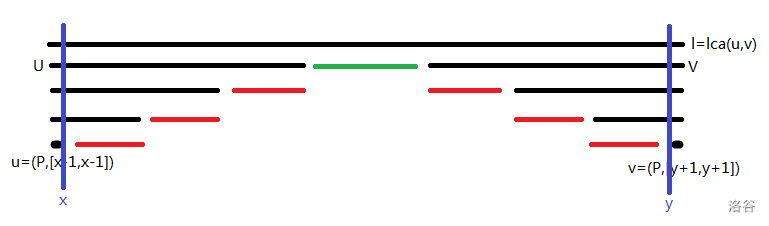
(黑色线段表示一个节点,红色,绿色线段表示需要统计的区间)
对于红色线段:
对于所有
同理,对于所有
定义
对于绿色线段:
设
则转化为求
比较不理解为什么 7s,放根号过去?
CF526F *3000,这个也 *3000?加个强制在线绝对不止
区间最长连续段维护方法相同,这里不再赘述。
闲话
析合树是可以
所以 CF526F 和 CF997E(Tarjan 求 LCA)都是可以
但是看起来代码复杂度会巨大,先咕着。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具