第60课 二叉树的性质

1. 二叉树的深层性质

（1）性质1： 在二叉树的第i层最多有2^i-1个结点（i≥1）

　　①第1层最多有：2^1-1 = 1个结点

　　②第2层最多有：2^2-1 = 2个结点

　　③第3层最多有：2^3-1 = 4个结点

　　④……

（2）性质2：高度为k的二叉树，最多有2^k-1个结点（k≥0）（即满二叉树的情况）

　　①如果有一层，最多有1 = 2¹-1 = 1 个结点

　　②如果有两层，最多有1 +２ = 2^２-1 = ３个结点

　　③如果有三层，最多有1 +２ + 4 = 2³-1 = 7个结点

　　④……

（３）性质３：对任何一棵二叉树，如果其叶结点有n₀个，度为２的非叶结点有n₂个，则有：n₀ = n₂ + 1

 

（4）性质4：具有n个结点的完全二叉树的高度为⌊log₂𝑛⌋+1，其中（⌊x⌋不大于x的最大整数）。

证明：

       ①具有n个结点的完全二叉树的高度k，则

           2^k-1-1 <  n ≤ 2^k - 1 （前一项为k-1层的结点总数，后一项为k层的结点总数）

       ②因n取整数，所以  2^k-1 ≤ n <2^k

       ③取对数得：k - 1 ≤ log₂n < k 。

       ④因为k取整数，所以 k = ⌊log₂𝑛⌋ + 1

（5）性质5：如果一棵有n个结点的完全二叉树（其高度⌊log₂𝑛⌋+1），按层次对结点进行编号（从上到下，从左到右），对于任意结点i（1≤i≤n）有：

 

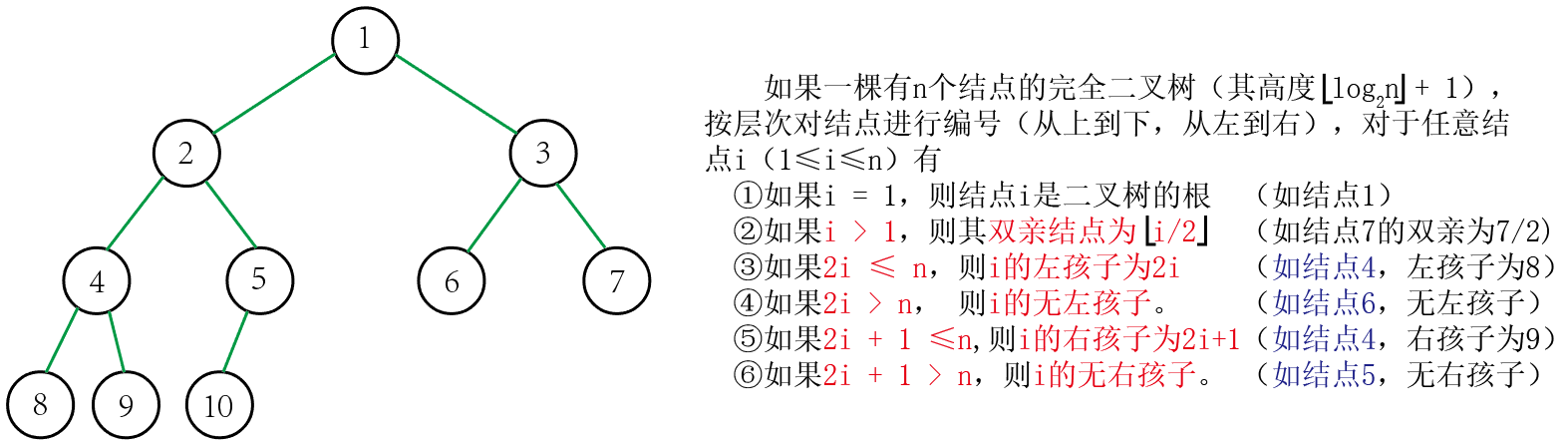
2. 二叉树性质的万能公式

（1）万能公式：第i层上最多结点数 = 前i–1层结点数总和 + 1

（2）用万能公式证明性质2

   证明：总结点数 = 第k层结点数 +  前k-1层结点总数

                       = 第k层结点数 + （第k层结点数 - 1）

                       = 2 * 第k层结点数 - 1  = 2 * (2^k-1 -1) - 1 = 2^k – 1