第41课 kmp子串查找算法

1. 朴素算法的改进

（1）朴素算法的优化线索

 

　　①因为 Pa != Pb 且Pb==Sb；所以Pa ！= Sb；因此在Sd处失配时，子串P右移1位比较没有意义，因为前面的比较己经知道了Pa ！= Sb，可以利用己经比较过的事实，而不必进行第2轮的比较，从而提高效率。

　　②KMP算法就是为解决这一问题而提出的！

（2）部分匹配与前后缀（以S字符串“ABCDAB”为例）

　　①前缀：除了最后一个字符以外，一个字符的全部头部组合的集合。如，字符串S的前缀有{A，AB，ABC，ABCD，ABCDA}，其中ABCDA为最大前缀。

　　②后缀：除第一个字符以外，一字符串的全部尾部组合的集合。字符串“ABCDAB”的后缀有{B，AB，DAB，CDAB，BCDAB}，其中BCDAB为最大后缀。

　　③部分匹配值：最长相同前缀和后缀的长度。如S串的最大相同前缀和后缀为“AB”。以下是“abxabxabc”字符串的部分匹配值示例：

模式串	a	b	x	a	b	x	a	b	c
部分匹配值	0	0	0	1	2	3	4	5	0

2. kmp字符匹配原理

（1）kmp算法中主要指针的移动规律

 

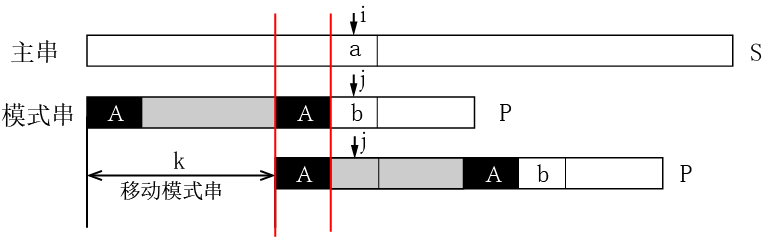
　　①kmp根据模式串本身携带的内部信息，在匹配失败时主串指针不回退，而是最大的移动模式串以减少匹配次数，而这依赖于部分匹配值表。

　　②失配时j指针的移动规律：在己经匹配的模式子串中，找出最大的相同前缀和后缀（A），然后移动并使它们重叠（如上图如示）。这一过程相当于将模式串j指针从当前位置b (后缀的下一个字符)左移到前缀的下一个字符的位置。

　　③而j指针要左移到的目标位置到底是在哪里，其数值被记录在next[j]中！（注意：next[j]表示当前部分匹配中最大相同前后缀的长度，也是匹配失败时j指针要移动到的目标位置）

（2）为什么匹配失败时，模式串指针可以从后缀一次性左移到前缀的下一个字符处？

　　①讨论1：假设下图蓝色部分不包含“ab”字符串

 

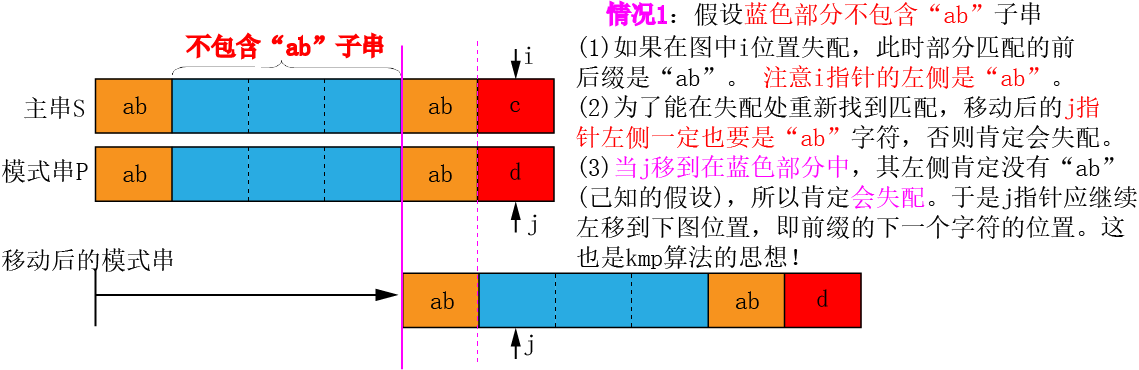
　　②讨论2：假设下图蓝色部分包含“ab”字符串

 

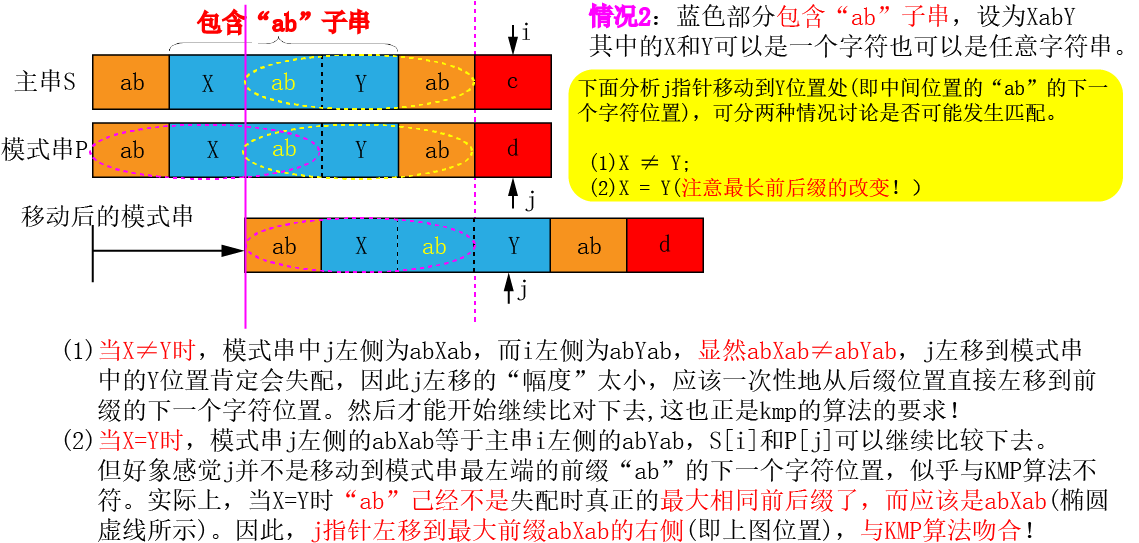
3. next数组

3.1 图解next数组：假设主串S，模式串P。

 

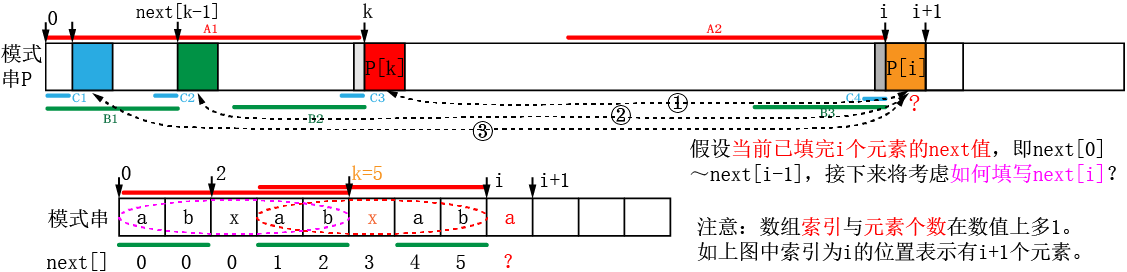
（1）假设当前已填写完i个元素的next值（即next[0]、next[1]…next[i-1]，注意元素个数与数组索引的不同！）。假设next[i-1]==k，其含义为在i左侧找到了一个最大相同前后缀（前缀为A1，后缀为A2，可得A1==A2），其长度为k。

（2）同理，填完k个元素的next值后，从next[k-1]可得k左侧的最大前后缀为B1和B2，所以B1=B2=B3。填完next[k]个元素之后，可得其前后缀C1==C2(=C3=C4)。

（3）问题转换为当在P[i]失配时，如何填写next[i]的值？从上面的分析可以看出，P[i]左侧的前后缀按长度从大到小依次为A2、B3、C4，这些前后缀可以拿来做文章。也就是P[i]的最大前后缀只可能在A2、B3、C4等基础上增加，实际上会按“A2→B3→C4→…”的顺序开始判断（贪心法，从最长串开始，不行则求其次）。

3.2 求解next数组过程

（1）动态规划（类似于数学归纳法）

　　①初始状态：k=0,j=0,next[0]=0。

　　②假设已经填完i个元素的next值（即next[0]、next[1]…next[i-1]）

　　③现在递推，当有i+1个元素时如何填写next[i]的值？

（2）求解　　

　　①如果此时P[i]==P[k]，前缀为A1+P[k]，后缀为A2+P[i]，显然两者相同。因此，next[i]填入 k + 1;（即在A2长度的基础上加1）

　　②如果P[i] != P[k]，表示此时的最大前后缀已经不可能是A2+P[i]了。按照贪心法，接下来会判断前后缀有没有可能是B3+P[i]，这需要对比②线两端的元素是否相同，先让k = next[k-1](其中next[k-1]表示B1（或B3）串的长度)，再判断此时的P[k](=P[next[k-1]])是否等于P[i]。如果相等，则最大前后缀就是B3+P[i]，next[i]=B3的长度+1，即此时的k+1。如果仍不相等，则判断前后缀有没有可能C4+P[i]，这时需对比③线再端的元素。如果相等，则next[i]=C4的长度加1，即当前的k+1。如果不相等，会去找更小的前后缀，然后一直对比下去，直到k==0时，表示没找到，next[i]的长度为0

【编程实验】

//main.cpp

#include <iostream>
#include <string.h>
using namespace std;

//部分匹配表（生成next数组）
void makeNext(const char* p, int next[])
{
    int len = strlen(p);

    //初始化状态
    int i = 0;
    int k = 0;
    next[0] = 0;

    for (i = 1; i<len; i++)   //从第2个字符开始
    {
        //找到p[i]之前可能的最大相同前后缀长度                      
        while ((k > 0) && (p[i] != p[k]))
            k = next[k - 1];

        //找到p[i]之前可能的最大前后缀以后，判断是否可以
        //在之个最大的前后缀加上p[i]这个字符
        if (p[i] == p[k]) {
            ++k;
        }

        next[i] = k;
    }
}

//kmp算法
int kmp(const char* t, const char* p)
{
    int tLen = strlen(t);
    int pLen = strlen(p);

    int ret = -1;
    
    if ( (t != NULL) && (p != NULL) && (tLen >= pLen) )
    {
        //创建next数组
        int* next = new int[pLen];
        makeNext(p, next);

        int j = 0;

        for (int i= 0; (j < pLen) && (i < tLen); i++)
        {
            while (( j > 0) && (t[i] != p[j]))
            {
                j = next[j]; //失配时，移动j到前缀后面。如果仍然失配，j一直往模式串
                             //开始处的方向移动，直到匹配或j到达了模式串开始的位置。
            }

            if (t[i] == p[j])   //匹配时，继续查找一下
                j++;            

            if (j == pLen)
               ret =  i - pLen + 1;        
        }

        delete next;
    }

    return ret;
}

int main(void)
{
    char t[] = "xyzababxabxab";
    //char t[] = "ababxabxabab";
    char p[] = "abxabxab";

    cout << kmp(t, p) << endl;

    return 0;
}

4. 小结

（1）部分匹配表是提高子串查找效率的关键

（2）部分匹配表定义为最大相同前缀和后缀的长度，也是失配时模式串指针要移动到的目标位置。

（3）可以用递推的方法产生部分匹配表

（4）KMP利用部分匹配值与子串指针移动的关系提高查找效率。