1. 用栈实现队列
(1)问题分析:用栈实现队列等价于用“后进先出”的特性实现“先进先出”的特性!
(2)解决方案

(3)实现思路:(准备两个栈用于实现队列:stack_in和stack_out)
①当有新元素入队时,将其压入stack_in
②当需要出队时:
A.如果stack_out.size()==0:
a.将stack_in中的元素逐一弹出并压入stack_out(元素转移)
b.将stack_out的栈顶元素弹出
B.如果stack_out.size()>0:将stack_out的栈顶元素弹出。
【编程实验】用栈实现队列
//main.cpp
#include <iostream> #include "LinkQueue.h" #include "LinkStack.h" using namespace std; using namespace DTLib; template <typename T> class StackToQueue : public Queue<T> { protected: mutable LinkStack<T> m_stack_in; mutable LinkStack<T> m_stack_out; //将stack_in中所有的元素移动到stack_out栈中 void move() const //O(n) { if(m_stack_out.size() == 0){ while(m_stack_in.size()>0){ m_stack_out.push(m_stack_in.top()); m_stack_in.pop(); } } } public: void enQueue(const T& elem)//O(1) { m_stack_in.push(elem); } void deQueue() //O(n) { //1. 判断并移动元素 move(); //2.出队列(出栈) if(m_stack_out.size() > 0){ m_stack_out.pop(); }else{ THROW_EXCEPTION(InvalidOperationException, "No element in current queue ..."); } } T front() const //O(n) { //1. 判断并移动元素 move(); //2.取栈顶元素 if(m_stack_out.size() > 0){ return m_stack_out.top(); }else{ THROW_EXCEPTION(InvalidOperationException, "No element in current queue ..."); } } void clear() //O(n) { m_stack_in.clear(); m_stack_out.clear(); } int length() const //O(1) { return m_stack_in.size() + m_stack_out.size(); } bool isEmpty() const //O(1) { return (length() == 0); } }; int main() { StackToQueue<int> sq; for(int i=0; i<10; i++){ sq.enQueue(i); } while(!sq.isEmpty()){ cout << sq.front() << " "; sq.deQueue(); } cout << endl; return 0; } /*输出结果 0 1 2 3 4 5 6 7 8 9 */
2. 用队列实现栈
(1)问题分析:本质上为用队列的“先进先出”特性实现栈的“后进先出”特性。
(2)解决方案
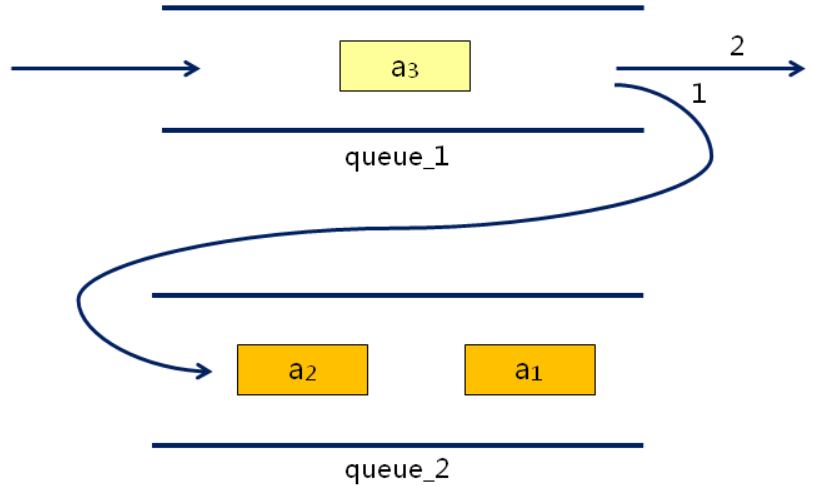
(3)实现思路:(准备两个队列用于类实现栈:queue1[in]和queue2[out])
①当有新元素入栈时,将其加入队列[in]
②当需要出栈时
A.将队列[in]中的n-1个元素出队列,并进入队列[out]中(元素转移)
B.将队列[in]中的最后一个元素出队列(出栈)
C.交换两个队列的角色:queue1[out]和queue2[in]
【编程实验】用队列实现栈
//main.cpp
#include <iostream> #include "LinkQueue.h" #include "LinkStack.h" using namespace std; using namespace DTLib; template <typename T> class QueueToStack : public Stack<T> { protected: LinkQueue<T> m_queue1; LinkQueue<T> m_queue2; LinkQueue<T>* m_pIn; LinkQueue<T>* m_pOut; //将in队列中的前n-1个元素转移到out队列中 void move() const //O(n) { int n = m_pIn->length() - 1; for(int i=0; i<n; i++){ m_pOut->enQueue(m_pIn->front()); m_pIn->deQueue(); } } //交换进出队列 void swap() //O(1) { LinkQueue<T>* temp = m_pIn; m_pIn = m_pOut; m_pOut = temp; } public: QueueToStack() //O(1) { m_pIn = &m_queue1; m_pOut = & m_queue2; } void push(const T& elem) //O(1) { m_pIn->enQueue(elem); } void pop() //O(n) { if(!m_pIn->isEmpty()){ //1. 转移元素 move(); //2.出栈 m_pIn->deQueue(); //3. 交换进出队列角色 swap(); }else{ THROW_EXCEPTION(InvalidOperationException, "No element in current stack ..."); } } T top() const //O(n) { if(!m_pIn->isEmpty()){ //1. 转移元素 move(); //2. 返回in队列的栈顶元素 return m_pIn->front(); }else{ THROW_EXCEPTION(InvalidOperationException, "No element in current stack ..."); } } void clear() //O(n) { m_queue1.clear(); m_queue2.clear(); } int size() const //O(1) { return m_queue1.length() + m_queue2.length(); } }; int main() { QueueToStack<int> qs; for(int i=0; i<10; i++){ qs.push(i); } while(qs.size() > 0){ cout << qs.top() << " "; qs.pop(); } cout << endl; return 0; } /*输出结果 9 8 7 6 5 4 3 2 1 0 */
3. 小结
(1)栈和队列在实现上非常类似,可以相互转化实现
(2)两个栈“后进先出”叠加得到“先进先出”的特性
(3)两个队列“先进先出”相互配合得到“后进先出”的特性
(4)栈和队列相互转化的学习有助于强化本质的理解。


