1. 常见时间复杂度
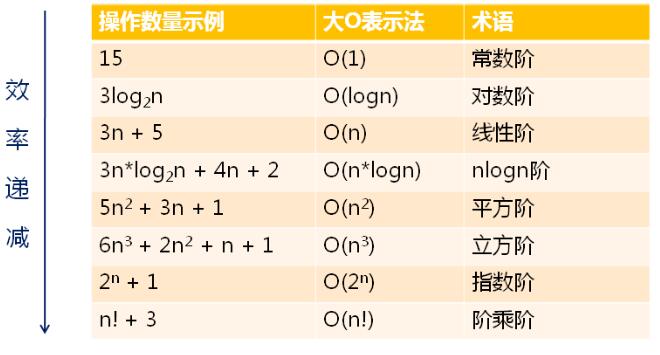
(1)O(1) < O(logn) < O(n) < O(n*logn) < O(n3) <O(2n) <O(n!) <O(nn)
(2)当算法的时间复杂度为O(2n),O(n!)或O(nn)时,即使n值很小,实际的程序运行时间也是不可接受的。
2. 算法的最好与最坏情况
(1)当算法在最坏情况下仍然能满足需求时,可以推断,算法的最好情况和平均情况都满足要求。
(2)数据结构课程中,在没有特殊说明时,所分析算法的时间复杂度都是指最坏时间复杂度。
3. 算法的空间复杂度(Space Complexity)
(1)定义:S(n) = O(f(n)) ==>类似地,时间复杂度记为:T(n) = O(f(n))
①n为算法的问题规模
②f(n)为空间使用函数,与n相关
(2)推导时间复杂度的方法同样适用于空间复杂度。如当算法所需要的空间是常数时,空间复杂度为S(1)
【计算练习】空间复杂度计算
//S(n) = O(1+n+1+1) = O(n) long sum(int n) { long ret = 0; //1 int* array = new int[n] //n for(int i=0; i<n; i++){ //1, for i array[i] = i + 1; } for(int i=0; i<n; i++){ //1,for i ret += array[i]; } delete[] array; return ret; }
4.空间与时间的策略
(1)多数情况下,算法的时间复杂度更令人关注
(2)如果有必要,可以通过增加额外的空间来降低时间复杂度
(3)同理,也可以通过增加算法的耗时降低空间复杂度。
【实例分析】空间换时间
/* 问题: 在一个由自然数1-1000中某些数字所组成的数组中,每个数字可能出现零次或多次 设计一个算法,找出出现次数最多的数字。 */ #include <iostream> using namespace std; void search(int a[], int len) //O(n) { int sp[1000] = {0}; int max = 0; //统计数组中每个数字出现的次数 for(int i=0; i<len; i++){ sp[a[i] - 1]++; } //找出最大次数 for(int i=0; i<1000; i++){ if(max < sp[i]){ max = sp[i]; } } //输出1-1000中出现次数最多的数(可能有多个) for(int i=0; i<1000; i++){ if(max == sp[i]){ cout << i + 1 << endl; } } } int main(int argc, char* argv[]) { int a[] = {1, 1, 3, 4, 5, 6, 6, 6, 3, 3}; search(a, sizeof(a)/sizeof(*a)); return 0; }
5. 小结
(1)一般而言,工程中使用的算法,时间复杂度不超过O(n3)
(2)算法分析与设计时,重点考虑最坏情况下的时间复杂度
(3)数据结构课程中重点关注算法的时间复杂度
(4)大O表示法同样适用于算法的空间复杂度
(5)空间换时间是工程开发中常用的策略


