【题解】Pavel and barbecue

目录

• 题目信息
  • 题目描述
  • 输入格式
  • 输出格式
  • 数据规模与约定
• 分析
• Code

本文同步发布于我的 洛谷博客。

题目信息

题目来源：8VC Venture Cup 2017 - Final Round，Codeforces；

在线评测地址：CF756A；

翻译：原创；

运行限制：\(2.00\ \textrm{s}/256\ \textrm{MiB}\)

题目描述

Pavel cooks barbecue. There are \(n\) skewers, they lay on a brazier in a row, each on one of \(n\) positions. Pavel wants each skewer to be cooked some time in every of \(n\) positions in two directions: in the one it was directed originally and in the reversed direction.

Pavel 在烤肉。共有 \(n\) 串烤肉排成一排，各自在 \(n\) 个位置中的一个。Pavel 希望每一串烤肉的每一面都能在每一个位置上烤过一次。

Pavel has a plan: a permutation \(p\) and a sequence \(b_{1},b_{2},...,b_{n}\), consisting of zeros and ones. Each second Pavel move skewer on position \(i\) to position \(p_{i}\), and if \(b_{i}\) equals \(1\) then he reverses it. So he hope that every skewer will visit every position in both directions.

Pavel 有一个全排列 \(p\) 和一个长为 \(n\) 的 0/1 序列 \(b\)。Pavel 每一步将位于 \(i\) 的串串移到 \(p_i\) 处。同时，如果 \(b_i=1\)，那么 Pavel 将反转这个串串。

Unfortunately, not every pair of permutation \(p\) and sequence \(b\) suits Pavel. What is the minimum total number of elements in the given permutation \(p\) and the given sequence \(b\) he needs to change so that every skewer will visit each of \(2n\) placements? Note that after changing the permutation should remain a permutation as well.

很不幸，不是每一对 \(p\) 和 \(b\) 都满足要求，Pavel 想知道最少修改多少个现有的 \(p\) 和 \(b\) 中的数才能满足自己的目的。注意修改后的序列也要满足要求。

It can be shown that some suitable pair of permutation \(p\) and sequence \(b\) exists for any \(n\).

易证这样的 \(p\) 和 \(b\) 对于所有的 \(n\) 都是存在的。

输入格式

第一行一个正整数 \(n\)，烤串的数量。

第二行 \(n\) 个正整数，分别表示 \(p_1,p_2,\cdots,p_n\)。

第三行 \(n\) 个正整数，分别表示 \(b_1,b_2,\cdots,b_n\)。

输出格式

一行一个正整数，表示最小的操作次数。

数据规模与约定

\(1\le p_i\le n\le 2\times 10^5\)，\(b_i\in \{0,1\}\)

分析

部分内容参考 官方题解。

---

这道题相当于有两个子问题：

1. 修改 \(p\)，使得每一个元素都可以根据 \(p\) 遍历所有位置；
2. 在 \(1\) 的基础上，修改 \(b\) 使得每一次遍历完毕后都会翻转一个面。

对于子问题 \(1\)，我们根据 \(p\) 构造有向基环树，我们的目标就是通过改变每一个节点的出边终点来使该基环树成为一个环。

样例 \(1\)：

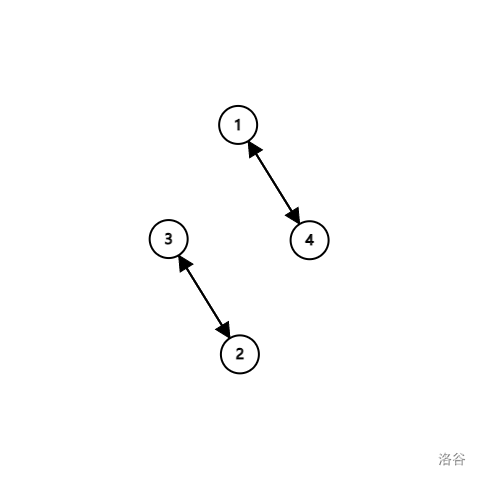
官方题解的解决方案是：如果只有一个环那么显然，否则操作数就是环的数量（根据面向数据编程，一个点应该也可以算作一个环）。

证明（伪证，大概意思应该就是这样）：

每个点的出度是 \(1\)，所以环和强连通分量等价。目标就是构造一个大小为 \(n\) 的强连通分量。

合并 \(n\) 个强连通分量的方法最少 \(n\) 步（环），方法如下：

对于第 \(i\) 个强连通分量（\(1\le i<n\)），选择任意一个节点，让其出边指向第 \(i+1\) 个强连通分量中的任意一个节点。

这样构造肯定可以强连通，证毕。

至于子问题 \(2\)，因为所有的节点都会被遍历一遍，所以只需要让 \(b\) 所有元素和为奇数即可，否则任意反转一个数即可。

最后答案就是两个子问题答案的和。

Code

#include <cstdio>
#include <cctype>
using namespace std;

const int max_n = 200000;

int a[max_n];
bool vis[max_n] = {};

#define gc getchar
inline int read() // 快读
{
	int c = gc(), t = 1, n = 0;
	while (isspace(c)) { c = gc(); }
	if (c == '-') { t = -1, c = gc(); }
	while (isdigit(c)) { n = n * 10 + c - '0', c = gc(); }
	return n * t;
}
#undef gc

int main()
{
	int n = read(), ptr, cnt = 0, ans = 0;

	for (int i = 0; i < n; i++)
		a[i] = read() - 1;
	for (int i = 0; i < n; i++) // 统计 b 和
		cnt += read();
	
	for (int i = 0; i < n; i++) // 数环
		if (!vis[i])
		{
			ptr = a[i], vis[i] = true;
			while (!vis[ptr])
				ptr = a[ptr];
			
			if (ptr == i) // 如果不是一个点
			{
				ptr = a[i];
				while (!vis[ptr])
				{
					vis[ptr] = true; // 整个环标记打上
					ptr = a[ptr];
				}
			}

			ans++; // 统计环的数量
		}
	
	if (ans == 1) // 只有一个就不用操作
		ans = 0;

	printf("%d\n", ans + !(cnt & 1)); // 输出

	return 0; // 然后就 AC 了、
}