python的多继承C3(mro)算法

多继承的继承顺序按照C3算法进行顺序继承

例一

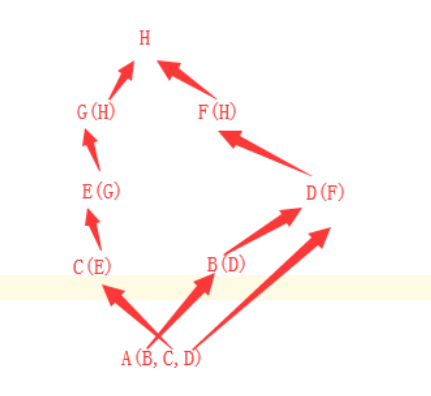
按照深度A类从左往右有三条可继承的"路"

先按照深度优先的算法,将每一路的每一个节点加到列表中

B = [B,D,F,H]

C = [C,E,G,H]

D = [D,F,H]

A = [B,C,D]　　A的广度顺序

得到四个列表,四个列表按照头尾的方式进行比较,如何划分头尾呢.

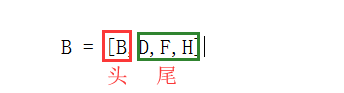
第一个为头,剩下的都是尾,

整体的算法介绍

　　比较第一个列表的头是都在其他列表中的尾部出现,如果出现,则跳过这个列表,直接到下一个列表的头部,再次判断是否出现在其他列表的尾部,如果都没有出现就将这个元素放进一个新的列表,

　　然后把所有列表中的这个元素删除,以此类推,直到把所有的列表删除为空,得出的新列表就是继承的顺序.

过程:

1   [B,D,F,H]  [C,E,G,H]  [D,F,H]  [B,C,D]	new_list[B,]
	第一次比较B,所有列表的尾部没有B,添加B到新列表,然后删除所有的头部B
2   [D,F,H]    [C,E,G,H]  [D,F,H]  [C,D]  	new_list[B,]
	比较头部D,D在其他的尾部中存在,跳过这次比较,直接进入下一个列表比较C
3   [D,F,H]    [E,G,H]  [D,F,H]  [D]		new_list[B,C]  
	C在其他列表的尾部不存在,将C添加至新列表,删除所有的头部C    
4   [F,H]    [E,G,H]  [F,H]  			new_list[B,C,D]
	再次回到第一个列表比较D,D没有存在其他列表的尾部添加D到新列表,然后删除所有的头部D
5   [H]    [E,G,H]  [H]				new_list[B,C,D,F]
6   [H]    [G,H]  [H]				new_list[B,C,D,F,E]
7   [H]    [H]  [H]				new_list[B,C,D,F,E,G]
8   []    []  []				new_list[B,C,D,F,E,G,H]

所以最后的继承顺序就是A,B,C,D,F,E,G,H,object

　　

例二

 

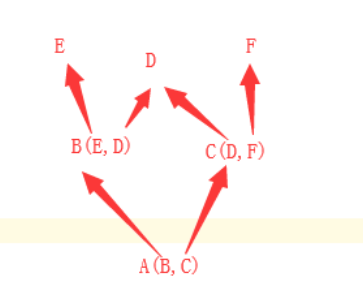
 流程:因为有多个分叉,所以需要先计算每一个分叉的mro顺序:

从最左边的最高杈开始计算它的mro

分叉B:[B] [B,E](父类的, 按照深度优先) [B,D](自己继承的按照广度优先)

计算结果:[B,E,D]

分叉C:[C] [C,D] [C,F]

计算结果:[C,D,F]

计算完上面的两个叉后,就变成了一个叉.

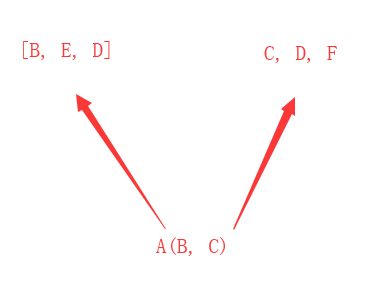
再次进行计算:

[A] [B, E, D] [C, D, F] [B, C]　　new_list[A,]

[] [E, D] [C, D, F] [C]　　new_list[A,B,]

[] [D] [C, D, F] [C]　　new_list[A,B,E,]

[] [D] [D, F] []　　new_list[A,B,E,C,]

[] [] [F] []　　new_list[A,B,E,C,D,]

[] [] [] []　　new_list[A,B,E,C,D,F]

所以最后的继承顺序就是A,B,E,C,D,F,object