数字金字塔升级版

【题目描述】

观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。

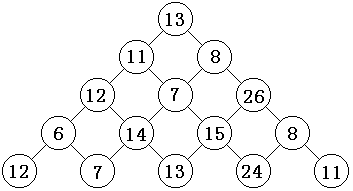
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。

【输入】

第一个行包含R(1≤ R≤1000)，表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

所有的被供应的整数是非负的且不大于100。

【输出】

单独的一行，包含那个可能得到的最大的和。

【输入样例】

5
13
11 8
12 7  26
6  14 15 8
12 7  13 24 11

【输出样例】

86

以上是数字金字塔1，现在加一个条件，要输出对100取模之后的最大值，那么能否在原本的状态转移方程上加上%100呢？显然不行，比如说98+1=99虽然比99+1=100小，但是对100取模之后，就变成了99和0，显然是99比较大，那应该怎么办呢？

多一个条件就多增加一维，将原来的数组f[i][j]=>f[i][j][k]，然后将int定义的数组改成bool数组，思路大致是这样的：i，j两个变量还是原本的含义，就是行列，新增加的变量k的意思是对100取模的结果，在0-99之间循环。那么a[i][j][k]

的含义就是第i行，第j列的数可不可以取到k，如果可以则赋值true，反之则赋值false

有了思路，代码自然很简单，这里只写下循环部分即可

代码：

for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
        for(int k=0;k<=99;k++)
        {
             if(f[i][j][k])
             {
                 f[i+1][j][(k+a[i+1][j])%100]=true;
                 f[i][j+1][(k+a[i][j+1])%100]=true;
             }
        }

然后最后再用一个99-0的循环来检验最值即可