KMP

记录
18:16 2024-2-5

目录

• 1.KMP

1.KMP

---

先把我之前学时候的笔记拉过来 数据结构学习第二十三天

串的模式匹配(KMP算法)

给定一段文本，从中找出某个指定的关键字

目标

　　给定一段文本:$ string=s_0s_1.....s_{n-1}$

　　给定一个模式:$ pattern=p_0p_1......p_{m-1}$

　　求\(pattern\)在\(string\)中出现的位置

简单实现

　　方法1:c的库函数 strstr

简单改进

　　方法2:从末尾开始比

大师改进

　　方法3:KMP(Knuth、Morris、Pratt)算法

　　将时间复杂度从\(T=O(nm) 改进到 T=O(n+m)\)

$ match(j)=\begin{cases} 满足p_0.....p_i=p_{j-i}....p_j的最大i(<j) \ -1 如果这样的i不存在 \end{cases} $

KMP算法 (这算法惊艳到我了)

总的来说,在每次比较失败时 下一次到可以匹配的时候是将已经匹配成功的序列中 从头开始的与从尾开始子列中可以匹配的最大部分 将头部移动到尾部 再进行比较 这样的话 对于给定的string文本的指针 不会向后移动 使得这个算法高效

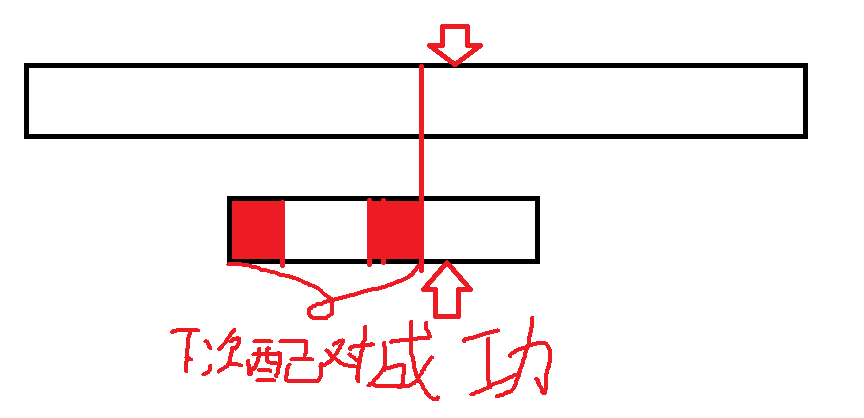
之前写的

点击查看代码

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define NotFound -1

typedef int Position;

void BuildMatch(char* pattern, int* match)
{
    Position i, j;
    int m = strlen(pattern);
    match[0] = -1;
    for (j = 1; j < m; j++)
    {
        i = match[j - 1];
        while (i >= 0 && pattern[i + 1] != pattern[j])
            i = match[i];
        if (pattern[i + 1] == pattern[j])
            match[j] = i + 1;
        else
            match[j] = -1;
    }
}

Position KMP(char* string, char* pattern)
{
    int n = strlen(string);
    int m = strlen(pattern);
    Position s, p, * match;

    if (n < m)return NotFound;
    match = (Position*)malloc(sizeof(Position) * m);
    BuildMatch(pattern, match);
    s = p = 0;
    while (s<n&&p<m)
    {
        if (string[s] == pattern[p])
        {
            s++; p++;
        }
        else if (p > 0)
            p = match[p - 1] + 1;
        else
            s++;
    }
    return (p == m) ? (s - m) : NotFound;
}

int main()
{
    char string[] = "This is a simple example";
    char pattern[] = "simple";
    Position p = KMP(string, pattern);
    if (p == NotFound)printf("Not Found.\n");
    else printf("%s\n", string + p);
    return 0;
}

---

书上比较简便的写法, 字符串下标从1开始，到n结束，即[1,n]

点击查看代码

// KMP
next[1] = 0;
for (int i = 2, j = 0; i <= n; i++) {
	while (j > 0 && a[i] != a[j+1]) j = next[j];
	if (a[i] == a[j+1]) j++;
	next[i] = j;
}

for (int i = 1, j = 0; i <= m; i++) {
	while (j > 0 && (j == n || b[i] != a[j+1])) j = next[j];
	if (b[i] == a[j+1]) j++;
	f[i] = j;
	// if (f[i] == n)，此时就是A在B中的某一次出现
}

// KMP 下标从0开始
next[0] = -1;
for (int i = 1, j = -1; i < N; i++) {
    while (j >= 0 && str[i] != str[j+1]) j = next[j];
    if (str[i] == str[j+1]) j++;
    next[i] = j;
}

for (int i = 0, j = -1; i < M; i++) {
	while (j >= 0 && (j == n - 1 || tar[i] != str[j+1])) j = next[j];
	if (tar[i] == str[j+1]) j++;
	f[i] = j;
	// if (f[i] == n - 1)，此时就是A在B中的某一次出现
}