数据结构学习第二十三天
19:04:41 2019-09-17
已知的查找方式
顺序查找 $O(N)$
二分查找(静态查找) $O(LogN)$
二叉搜索树 $O(h)$ h为二叉查找树的高度
平衡二叉树 $O(LogN)
查找的本质:已知对象找位置
有序安排对象:全序(二分查找) 半序(二叉搜索树)
直接“算出”对象位置:散列
散列查找法的两项基本工作:
计算位置:构造散列函数 确定关键词存储位置
解决冲突:引用某种策略 解决多个关键词位置相同的问题
时间复杂度几乎是常量:$O(1)$,及查找时间与问题规模无关
散列表(哈希表)
类型名称:符号表(SymbolTable)
数据对象集:符号表是"名字(Name)-属性(Attribute)"的集合
如果没有溢出 $T_查询=T_插入=T_删除=O(1)$
”散列(Hashing)"的基本思想是:
(1)以关键字Key为自变量,通过一个确定的函数h(散列函数) 计算出对应的函数值h(Key),作为数据对象的存储地址
(2)可能不同的关键字会映射到同一个散列地址上,
即$h(key_1)=h(key_2) 当(key_1\not=key_2)$,称为“冲突(Collision)”---------需要某种冲突解决策略
散列函数的构造方法
一个好的散列函数一般应考虑下列两个因素:
1.计算简单,以便提高转换速度
2.关键词对应的 地址空间分布均匀,以尽量减少冲突
数字关键词的散列函数构造
1.直接定址法
取关键词的某个线性函数值为散列地址,即$h(key)=a*key+b (a、b为常数)$
2.除留余数法
散列函数为 $h(key)=key mod p$
这里 $p=TableSize$
一般,$p$取素数
3.数字分析法
4.折叠法
把关键词分割成位数相同的几个部分,然后叠加
5.平方取中法
字符关键词的散列函数构造
1.一个简单的散列函数-----ASCII码加和法
对字符型关键词key定义散列函数如下:
$h(key)=(\sum key[i]) mod TableSize$
2.简单的改进------前3个字符移位法
$h(key)=(key[0]*27^2+key[1]*27+key[2])mod TableSize$
3.好的散列函数------移位法
涉及关键词所有n个字符,并且分布得很好:
$h(key)=\Big (\sum_{i=0}^{n-1} key[n-i-1]*32^i \Big) mod TableSize
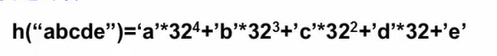
冲突处理方法
常用的思路
换个位置:开放地址法
同一位置的冲突对象组织在一起:链地址法
开放地址法(Open Addressing)
一旦产生了冲突(该地址已有其它元素),就按某种规则取寻找另一空地址
若发生了第i次冲突,试探的下一个地址将增加$d_i$,基本公式是
$h_i(key)=(h(key)+d_i)mod TableSize (1\leq i \les TableSize)$
$d_i$决定了不同的解决冲突方案:线性探测、平方探测、双散列
线性探测:$d_i=i$
平方探测:$d_i=\pm i^2$
双散列:$d_i=i*h_2(key)$
1.线性探测法(Linear Probing)
以增量序列$1,2,3,4,.......,(TableSize-1)$循环试探下一个存储地址 (线性探测很容易聚集)
2.平方探测法(Quadratic Probing) ----二次探测
平方探测法:以增量序列$1^2,-1^2,2^2,-2^2,......,q^2,-q^2$且$q\leq TableSize/2$循环试探下一个存储地址
有定理显示:如果散列表长度TabLeSize是某个$4k+3$(k是正整数)形式的素数时,平方探测法就可以探查到整个散列表空间
在开发地址散列表中,删除操作要很小心,通常只能懒惰删除,即需要增加一个"删除标记(Deleted)“,而并不是真正删除它,以便查找时不会"断链",其空间可以在下次插入时重用
3.双散列探测法(Double Hashing)
双散列探测法:$d_i为i*h_2(key),h_2(key)是另一个散列函数$
探测序列成$h_2(key),2h_2(key),3h_2(key),.......$
$对任意的key,h_2(key) \not=0$
探测序列还应该保证所有的散列存储单元都应该能被探测到
选择以下形式
$h_2(key)=p-(key mod p)$
其中 $p<TableSize,p、TableSize 都是素数$
4.再散列(Rehashing)
当散列表元素太多(即装填因子 $\alpha A$太大)时,查找效率会下降
实用最大装填因子一般取$ 0.5\leq \alpha A \leq0.85$
散列表扩大时,原有元素需要重新计算放置到新表中
分离链接法(Separate Chainig)
将相应位置上冲突的所有关键词存储在同一个单链表中
开放地址法的实现

1 //创建开放定址法的散列表实现 2 #include<stdio.h> 3 #include<math.h> 4 #include<malloc.h> 5 #define MAXTABLESIZE 100000 //允许开辟的最大散列表长度 6 typedef int ElementType; //关键词类型使用整型 7 typedef int Index; //散列地址类型 8 typedef Index Position; //数据所在位置与散列地址是同一类型 9 /*散列单元状态类型,分别对象:有合法元素、空单元、有已删除元素*/ 10 typedef enum{Legitimate,Empty,Deleted}EntryType; 11 typedef struct HashEntry Cell; //散列表单元类型 12 struct HashEntry 13 { 14 ElementType Data; //存放元素 15 EntryType Info; //单元状态 16 }; 17 18 typedef struct TblNode* HashTable; //散列表类型 19 struct TblNode //散列表节点定义 20 { 21 int TableSize; //表的最大长度 22 Cell* Cells; //存放散列单元数据的数组 23 }; 24 25 int NextPrime(int N) 26 {//返回大于N且不超过MAXTABLESIZE的最小素数 27 int i, p = (N % 2) ? N + 2 : N + 1; //从大于N的下一个奇数开始 28 while (p<=MAXTABLESIZE) 29 { 30 for (i = (int)sqrt(p); i > 2; i--) 31 if (p % i == 0)break; //p不是素数 32 if (i == 2)break; //p是素数 结束循环 33 else 34 p += 2; //试探下一个素数 35 } 36 return p; 37 } 38 39 HashTable CreateTable(int TableSize) 40 { 41 HashTable H; 42 int i; 43 H = (HashTable)malloc(sizeof(struct TblNode)); 44 //保证散列表最大长度是素数 45 H->TableSize = NextPrime(TableSize); 46 //声明单元数组 47 H->Cells = (Cell*)malloc(sizeof(ElementType) * H->TableSize); 48 //初始化单元状态为"空单元" 49 for (i = 0; i < H->TableSize; i++) 50 H->Cells[i].Info = Empty; 51 return H; 52 } 53 54 int Hash(ElementType Key, int TableSize) 55 { 56 return Key % TableSize; 57 } 58 //平方探测法的查找与插入 59 Position Find(HashTable H, ElementType Key) 60 { 61 Position CurrentPos, NewPos; 62 int CNum = 0; 63 NewPos = CurrentPos = Hash(Key, H->TableSize); 64 while (H->Cells[NewPos].Info!=Empty&&H->Cells[NewPos].Data!=Key) 65 { 66 //统计冲突次数 并且判断奇偶次 67 if (++CNum % 2) 68 {//奇数次 69 NewPos = CurrentPos + (CNum / 2) * (CNum / 2); 70 while (NewPos >= H->TableSize) 71 NewPos -= H->TableSize; //调整为合法地址 72 } 73 else 74 {//偶数次 75 NewPos = CurrentPos - (CNum / 2) * (CNum / 2); 76 while (NewPos < 0) 77 NewPos += H->TableSize; //调整为合法地址 78 } 79 } 80 return NewPos; 81 } 82 83 void Insert(HashTable H, ElementType Key) 84 { 85 Position Pos = Find(H, Key); 86 if (H->Cells[Pos].Info != Legitimate) 87 { 88 H->Cells[Pos].Data = Key; 89 H->Cells[Pos].Info = Legitimate; 90 } 91 }
链地址法的实现

1 #include<stdio.h> 2 #include<malloc.h> 3 #include<math.h> 4 #include<string.h> 5 #define KEYLENGTH 15 //关键词字符串最大长度 6 #define MAXTABLESIZE 10000 7 8 typedef char ElementType[KEYLENGTH + 1]; //关键词类型用字符串 9 typedef int Index; //散列地址类型 10 11 typedef struct LNode* PtrToLNode; 12 struct LNode 13 { 14 ElementType Data; 15 PtrToLNode Next; 16 }; 17 typedef PtrToLNode Position; 18 typedef PtrToLNode List; 19 20 typedef struct TblNode* HashTable; //散列表类型 21 struct TblNode //散列表节点定义 22 { 23 int TableSize; //表的最大长度 24 List Heads; //指向链表头节点的数组 25 }; 26 27 int NextPrime(int N) 28 { 29 int i; 30 int p = (N % 2)?N + 2:N + 1; 31 while (p<MAXTABLESIZE) 32 { 33 for (i = (int)sqrt(p); i > 2; i--) 34 if (p % i)break; 35 if (i == 2)break; 36 else 37 p += 2; 38 } 39 return p; 40 } 41 int Hash(ElementType Key, int TableSize) 42 { 43 44 } 45 HashTable CreateTable(int TableSize) 46 { 47 HashTable H; 48 int i; 49 50 H = (HashTable)malloc(sizeof(struct TblNode)); 51 //保证散列表的最大长度是素数 52 H->TableSize = NextPrime(TableSize); 53 54 //分配链表头节点数组 55 H->Heads = (List)malloc(H->TableSize * (struct LNode)); 56 //初始化表头节点 57 for (i = 0; i < H->TableSize; i++) 58 { 59 H->Heads[i].Data[0] = '\0'; 60 H->Heads[i].Next = NULL; 61 } 62 return H; 63 } 64 65 Position Find(HashTable H, ElementType Key) 66 { 67 Position P; 68 Index Pos; 69 70 Pos = Hash(Key, H->TableSize); 71 P = H->Heads[Pos].Next; //从链表的第一个节点开始 72 while (P && P->Data != Key) 73 P = P->Next; 74 return P; 75 } 76 77 void Insert(HashTable H, ElementType Key) 78 { 79 Position P, NewCell; 80 Index Pos; 81 P = Find(H, Key); 82 if (!P) //关键词未找到 可以插入 83 { 84 NewCell = (Position)malloc(sizeof(struct LNode)); 85 strcpy(NewCell->Data, Key); 86 Pos = Hash(Key, H->TableSize); //初始散列位置 87 NewCell->Next = H->Heads[Pos].Next;//将NewCell插入为H->Heads[Pos]链表的第一个节点 88 H->Heads[Pos].Next = NewCell; 89 } 90 } 91 92 void DestroyTable(HashTable H) 93 { 94 int i; 95 Position P, Tmp; 96 for (int i = 0; i < H->TableSize; i++) 97 { 98 P = Tmp = H->Heads[i].Next; 99 while (Tmp) 100 { 101 free(P); 102 P = Tmp->Next; 103 Tmp = P; 104 } 105 } 106 free(H->Heads); 107 free(H); 108 }
串:线性存储的一组数据(默认是字符)
特殊操作集合
求串的长度
比较两串是否相等
两串相接
求子串
插入子串
匹配子串
删除子串
串的模式匹配(KMP算法)
给定一段文本,从中找出某个指定的关键字
目标
给定一段文本:$ string=s_0s_1.....s_{n-1}$
给定一个模式:$ pattern=p_0p_1......p_{m-1}$
求$pattern$在$string$中出现的位置
简单实现
方法1:c的库函数 strstr
简单改进
方法2:从末尾开始比
大师改进
方法3:KMP(Knuth、Morris、Pratt)算法
将时间复杂度从$T=O(nm) 改进到 T=O(n+m)$
$ match(j)=\begin{cases} 满足p_0.....p_i=p_{j-i}....p_j的最大i(<j) \\ -1 如果这样的i不存在 \end{cases} $
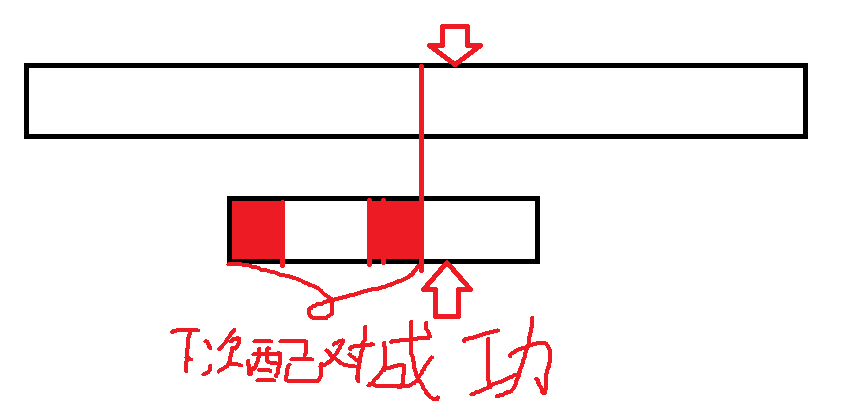
KMP算法 (这算法惊艳到我了)
总的来说,在每次比较失败时 下一次到可以匹配的时候是将已经匹配成功的序列中 从头开始的与从尾开始子列中可以匹配的最大部分 将头部移动到尾部 再进行比较 这样的话 对于给定的string文本的指针 不会向后移动 使得这个算法高效

1 #include<stdio.h> 2 #include<string.h> 3 #include<stdlib.h> 4 #define NotFound -1 5 6 typedef int Position; 7 8 void BuildMatch(char* pattern, int* match) 9 { 10 Position i, j; 11 int m = strlen(pattern); 12 match[0] = -1; 13 for (j = 1; j < m; j++) 14 { 15 i = match[j - 1]; 16 while (i >= 0 && pattern[i + 1] != pattern[j]) 17 i = match[i]; 18 if (pattern[i + 1] == pattern[j]) 19 match[j] = i + 1; 20 else 21 match[j] = -1; 22 } 23 } 24 25 Position KMP(char* string, char* pattern) 26 { 27 int n = strlen(string); 28 int m = strlen(pattern); 29 Position s, p, * match; 30 31 if (n < m)return NotFound; 32 match = (Position*)malloc(sizeof(Position) * m); 33 BuildMatch(pattern, match); 34 s = p = 0; 35 while (s<n&&p<m) 36 { 37 if (string[s] == pattern[p]) 38 { 39 s++; p++; 40 } 41 else if (p > 0) 42 p = match[p - 1] + 1; 43 else 44 s++; 45 } 46 return (p == m) ? (s - m) : NotFound; 47 } 48 49 int main() 50 { 51 char string[] = "This is a simple example"; 52 char pattern[] = "simple"; 53 Position p = KMP(string, pattern); 54 if (p == NotFound)printf("Not Found.\n"); 55 else printf("%s\n", string + p); 56 return 0; 57 }
PTA第34题 简单的利用KMP算法的一道题

1 #define _CRT_SECURE_NO_WARNINGS 2 #include<stdio.h> 3 #include<stdlib.h> 4 #include<string.h> 5 #define NotFount -1 6 7 typedef int Position; 8 9 void BuildMatch(char* pattern, int* match) 10 { 11 Position i, j; 12 int m = strlen(pattern); 13 match[0] = -1; 14 for (int j = 1; j < m; j++) 15 { 16 i = match[j - 1]; 17 while (i >= 0 && pattern[i + 1] != pattern[j]) 18 i = match[i]; 19 if (pattern[i + 1] == pattern[j]) 20 match[j] = i + 1; 21 else 22 match[j] = -1; 23 } 24 } 25 26 Position KMP(char* string, char* pattern) 27 { 28 int n = strlen(string); 29 int m = strlen(pattern); 30 Position s, p; 31 Position* match; 32 match = (Position*)malloc(sizeof(Position) * m); 33 BuildMatch(pattern, match); 34 s = p = 0; 35 while (s<n&&p<m) 36 { 37 if (string[s] == pattern[p]) 38 { 39 s++; 40 p++; 41 } 42 else if (p > 0) 43 p = match[p - 1] + 1; 44 else 45 s++; 46 } 47 return (p == m) ? (s - m) : NotFount; 48 } 49 50 int main() 51 { 52 char* string = (char*)malloc(sizeof(char) * 1000000); 53 int n; 54 scanf("%s%d", string,&n); 55 while (n--) 56 { 57 char* pattern = (char*)malloc(sizeof(char) * 100000); 58 scanf("%s", pattern); 59 Position p; 60 p = KMP(string, pattern); 61 if (p == NotFount) 62 printf("P----Not Found\n"); 63 else 64 printf("P----%s\n", string + p); 65 } 66 return 0; 67 }
PTA 第29题 表排序思想的应用
代码1 有一个测试点运行超时

1 #define _CRT_SECURE_NO_WARNINGS 2 #include<stdio.h> 3 4 int A[100000] = { 0 }; 5 int Position[100000] = { 0 }; 6 int IsRight[100000] = { 0 }; 7 void Swap(int i, int j) 8 { 9 int tmp = A[i]; 10 A[i] = A[j]; 11 A[j] = tmp; 12 } 13 int SwapTimes=0; 14 int IsOk(int N) 15 { 16 for (int i = 1; i < N; i++) 17 if (IsRight[i] != 1) 18 return i; 19 return 0; 20 } 21 void Charge(int N) 22 { 23 int t; 24 while (1) 25 { 26 27 if (/*A[0] == 0*/Position[0]==0) 28 { 29 t = IsOk(N); 30 if (!t) 31 break; 32 //Swap(Position[0], Position[i]); //可以不用交换 作好标记即可 33 int temp = Position[0]; //交换这两个元素的位置 34 Position[0] = Position[t]; 35 Position[t] = temp; 36 SwapTimes++; 37 } 38 //Swap(Position[0], Position[Position[0]]); 39 IsRight[Position[0]] = 1; 40 Position[0] = Position[Position[0]]; 41 SwapTimes++; 42 } 43 } 44 int main() 45 { 46 int N; 47 scanf("%d", &N); 48 for (int i = 0; i < N; i++) 49 { 50 int num; 51 scanf("%d", &num); 52 A[i] = num; 53 Position[num] = i; 54 if (A[i] == i) 55 IsRight[i] = 1; 56 } 57 Charge(N); 58 printf("%d", SwapTimes); 59 return 0; 60 }
代码2 这个正确
是利用表的物理排序时 N个数字的排列由若干个独立的环组成
对于含有0元素的 环来说 交换次数 为 环内元素减一
对于不含有0元素的 环来说 交换次数 为 环内元素加一(0元素)减一(公式)再加一(将0元素添加到环中)

1 #define _CRT_SECURE_NO_WARNINGS 2 #include<stdio.h> 3 4 int A[100000] = { 0 }; 5 int Position[100000] = { 0 }; 6 int IsRight[100000] = { 0 }; 7 void Swap(int i, int j) 8 { 9 int tmp = A[i]; 10 A[i] = A[j]; 11 A[j] = tmp; 12 } 13 int SwapTimes=0; 14 int FindElements(int Pos) 15 { 16 int num=1; 17 while (Position[Pos]!=Pos) 18 { 19 num++; 20 IsRight[Position[Pos]] = 1; 21 Position[Pos] = Position[Position[Pos]]; 22 } 23 return num; //返回元素的个数 24 } 25 void Charge(int N) 26 { 27 int num; 28 //从零开始计算 29 SwapTimes += FindElements(0)-1; //交换次数比元素个数少一 30 for (int i = 1; i < N; i++) 31 { 32 if (!IsRight[i]) 33 SwapTimes += FindElements(i)+1; //虽然交换次数比元素个数少一 但是要利用0来进行交换 所以时 这个环的元素加一 34 } //而把0元素添加到 环中先进行一次交换 所以 最后结果为 元素+1-1+1 35 } 36 int main() 37 { 38 int N; 39 scanf("%d", &N); 40 for (int i = 0; i < N; i++) 41 { 42 int num; 43 scanf("%d", &num); 44 A[i] = num; 45 Position[num] = i; 46 if (A[i] == i) 47 IsRight[i] = 1; 48 } 49 Charge(N); 50 printf("%d", SwapTimes); 51 return 0; 52 }
PTA第28题 表排序的应用 有几个测试点死活过不了

1 #define _CRT_SECURE_NO_WARNINGS 2 #include<stdio.h> 3 struct User 4 { 5 int Score[6]; 6 int TotalScore; 7 int PrefectProblems; 8 int IsSubmit[6]; 9 }Users[10000]; 10 int Problem_Full_Score[6]; 11 int Table[10000]; 12 void Print(int N,int K) 13 { 14 int issubmit = 0; 15 int j = 1; 16 int x = 1; 17 for (int i = 1; i <= N; i++) 18 { 19 if (Users[Table[i]].TotalScore == 0) 20 break; 21 /*for (int k = 1; k <= K; k++) 22 { 23 if (Users[Table[i]].IsSubmit[k]) 24 issubmit = 1; 25 } 26 if (!issubmit) 27 continue;*/ 28 if (Users[Table[i]].TotalScore == Users[Table[i - 1]].TotalScore) 29 printf("%d %05d %d", j, Table[i], Users[Table[i]].TotalScore); 30 else 31 { 32 j = x; 33 printf("%d %05d %d", i, Table[i], Users[Table[i]].TotalScore); 34 x++; 35 } 36 for (int m = 1; m <= K; m++) 37 { 38 if (Users[Table[i]].Score[m]) 39 printf(" %d", Users[Table[i]].Score[m]); 40 else if (!Users[Table[i]].IsSubmit[m]) 41 printf(" -"); 42 else 43 printf(" 0"); 44 } 45 printf("\n"); 46 } 47 } 48 void InitializeTable(int N) 49 { 50 for (int i = 1; i <= N; i++) 51 Table[i] = i; 52 } 53 void Table_Sort(int N) 54 { 55 for (int i = 2; i <= N; i++) 56 { 57 int p=i; 58 int Temp = Users[Table[p]].TotalScore; 59 int Prefect = Users[Table[p]].PrefectProblems; 60 for (; p > 1 &&(Users[Table[p - 1]].TotalScore < Temp||(Users[Table[p-1]].TotalScore==Temp&&Users[Table[p-1]].PrefectProblems<Prefect)|| (Users[Table[p - 1]].TotalScore == Temp && Users[Table[p - 1]].PrefectProblems==Prefect&&Table[p]>i)); p--) 61 { 62 Table[p] = Table[p - 1]; 63 } 64 Table[p] = i; 65 } 66 } 67 int main() 68 { 69 int N, K, M; 70 scanf("%d %d %d", &N, &K, &M); 71 for (int i = 1; i <= K; i++) 72 { 73 int Score = 0; 74 scanf("%d", &Score); 75 Problem_Full_Score[i] = Score; 76 } 77 for (int i = 0; i < M; i++) 78 { 79 int Use_id, Problem_id, Partial_Score_Obtained; 80 scanf("%d %d %d", &Use_id, &Problem_id, &Partial_Score_Obtained); 81 Users[Use_id].IsSubmit[Problem_id] = 1; 82 if (Users[Use_id].Score[Problem_id] < Partial_Score_Obtained) 83 { 84 Users[Use_id].TotalScore += Partial_Score_Obtained - Users[Use_id].Score[Problem_id]; 85 Users[Use_id].Score[Problem_id] = Partial_Score_Obtained; 86 if (Partial_Score_Obtained == Problem_Full_Score[Problem_id]) 87 Users[Use_id].PrefectProblems++; 88 } 89 } 90 InitializeTable(N); 91 Table_Sort(N); 92 Print(N,K); 93 return 0; 94 }
PTA第30题 一道直白的利用散列的题
把情况考虑清除后就没什么要注意的点

1 #define _CRT_SECURE_NO_WARNINGS 2 #include<stdio.h> 3 #include<malloc.h> 4 #include<math.h> 5 #include<stdlib.h> 6 #include<string.h> 7 #define KEYLENGTH 11 //关键词类型长度 8 #define MAXTABLESIZE 200000 9 10 typedef char ElementType[KEYLENGTH+1]; 11 typedef struct LNode* PtrToNode; 12 int Persons; 13 struct LNode 14 { 15 ElementType Data; 16 PtrToNode Next; 17 int Times; 18 }; 19 typedef PtrToNode List; 20 typedef PtrToNode Position; 21 22 typedef struct HblNode* HashTable; 23 struct HblNode 24 { 25 int TableSize; 26 List Heads; 27 }; 28 int NextPrime(int N) 29 { 30 int i; 31 int p = (N % 2) ? N + 2 : N + 1; //检测奇数 32 while (p<MAXTABLESIZE) 33 { 34 for (i = (int)sqrt(p); i > 2; i--) 35 if (p % i == 0) 36 break; 37 if (i == 2)break; 38 else 39 p += 2; 40 } 41 return p; 42 } 43 int Hash(ElementType Key, int TableSize) 44 { 45 return atoi(Key + 7) % TableSize; 46 } 47 long Atoi(ElementType S, int N) 48 { 49 long num=0; 50 for (int i = 0; i < N; i++) 51 { 52 num += num * 10 + S[i] - '0'; 53 } 54 return num; 55 } 56 HashTable CreateHashTable(int TableSize) 57 { 58 HashTable H; 59 H = (HashTable)malloc(sizeof(struct HblNode)); 60 H->TableSize = NextPrime(TableSize); 61 H->Heads = (List)malloc(H->TableSize * sizeof(struct LNode)); 62 for (int i = 0; i < H->TableSize; i++) 63 { 64 H->Heads[i].Data[0] ='\0'; 65 H->Heads[i].Next = NULL; 66 H->Heads[i].Times = 0; 67 } 68 return H; 69 } 70 Position Find(HashTable H, ElementType Key) 71 { 72 int Pos; 73 Position P; 74 Pos= Hash(Key, H->TableSize); 75 P = H->Heads[Pos].Next; 76 while (P && strcmp(P->Data, Key)) 77 P = P->Next; 78 return P; 79 } 80 void Insert(HashTable H, ElementType Key) 81 { 82 Position P = Find(H, Key); 83 PtrToNode NewCell; 84 if (!P) 85 { 86 int Pos = Hash(Key, H->TableSize); 87 NewCell = (PtrToNode)malloc(sizeof(struct LNode)); 88 NewCell->Next = H->Heads[Pos].Next; 89 H->Heads[Pos].Next = NewCell; 90 strcpy(NewCell->Data, Key); 91 NewCell->Times = 1; 92 } 93 else 94 P->Times++; 95 } 96 void JudgeAndPrint(HashTable H) 97 { 98 Position MaxP=(Position)malloc(sizeof(struct LNode)); 99 MaxP->Times =0; 100 Position P=NULL; 101 for (int i = 0; i < H->TableSize; i++) 102 { 103 P = H->Heads[i].Next; 104 while (P) 105 { 106 if (P->Times > MaxP->Times) 107 { 108 Persons = 1; 109 MaxP = P; 110 } 111 else if (P->Times == MaxP->Times) 112 { 113 Persons++; 114 if (Atoi(P->Data,11) <Atoi(MaxP->Data,11)) 115 MaxP = P; 116 } 117 P = P->Next; 118 } 119 } 120 if(Persons==1) 121 printf("%s %d", MaxP->Data, MaxP->Times); 122 else if(Persons>1) 123 printf("%s %d %d", MaxP->Data, MaxP->Times,Persons); 124 } 125 int main() 126 { 127 int N; 128 scanf("%d", &N); 129 HashTable H = CreateHashTable(N); 130 for (int i = 0; i < N; i++) 131 { 132 char s1[12] = { 0 }, s2[12] = { 0 }; 133 scanf("%s %s", s1, s2); 134 Insert(H, s1); 135 Insert(H, s2); 136 } 137 JudgeAndPrint(H); 138 return 0; 139 }
PTA第31题 也是一道直白的利用散列的题
主要要考虑的是什么时候停止检测
因为是利用正向的二次探测 即增量为$1^2,2^2,3^2,.......,{TableSize}^2,.............$
经过分析可知 对于大于$TableSize$的增量来说
$(TableSize+CNum)^2={TableSize}^2+2*{CNum}*{TableSize}+{CNum}^2$
在调整之后 又变成了${CNum}^2$为增量来检测 那么之后的就是前面的重复了
故只需检测到${CNum}={TableSize-1}$即可

1 #define _CRT_SECURE_NO_WARNINGS 2 #include<stdio.h> 3 #include<malloc.h> 4 #include<math.h> 5 #define MAXTABLESIZE 20000 6 7 typedef int ElementType; 8 typedef enum { Legitimate, Empty, Deleted } EntryType; 9 typedef struct HashEntry Cell; 10 struct HashEntry 11 { 12 ElementType Data; 13 EntryType Info; 14 }; 15 16 typedef struct HblNode* HashTable; 17 struct HblNode 18 { 19 int TableSize; 20 Cell* Cells; 21 }; 22 23 int NextPrime(int N) 24 { 25 if (N == 1) 26 return 2; 27 int p = (N % 2) ? N + 2 : N + 1; 28 int i; 29 while (p<=MAXTABLESIZE) 30 { 31 for (i = (int)sqrt(p); i > 2; i--) 32 if (p % i == 0) 33 break; 34 if (i == 2)break; 35 else 36 p += 2; 37 } 38 return p; 39 } 40 int Hash(int Key, int TableSize) 41 { 42 return Key % TableSize; 43 } 44 HashTable CreateHashTable(int TableSize) 45 { 46 HashTable H; 47 H = (HashTable)malloc(sizeof(struct HblNode)); 48 H->TableSize = NextPrime(TableSize); 49 H->Cells = (Cell*)malloc(H->TableSize * sizeof(Cell)); 50 for (int i = 0; i < H->TableSize; i++) 51 H->Cells[i].Info = Empty; 52 return H; 53 } 54 55 int Find(HashTable H, ElementType Key) 56 { 57 int NewPos, CurPos; 58 int CNum = 0; 59 NewPos = CurPos = Hash(Key, H->TableSize); 60 while (H->Cells[NewPos].Info!=Empty&&H->Cells[NewPos].Data!=Key) 61 { 62 ++CNum; 63 int Flag = 0; 64 NewPos = CurPos+CNum * CNum; 65 if (CNum>H->TableSize) 66 return -1; 67 while (NewPos >= H->TableSize) 68 NewPos -= H->TableSize; 69 } 70 return NewPos; 71 } 72 73 int Insert(HashTable H, ElementType Key) 74 { 75 int Pos = Find(H, Key); 76 if (Pos ==-1) 77 return -1; 78 if (H->Cells[Pos].Info != Legitimate) 79 { 80 H->Cells[Pos].Data = Key; 81 H->Cells[Pos].Info = Legitimate; 82 } 83 return Pos; 84 } 85 86 int main() 87 { 88 int M, N; 89 scanf("%d %d", &M, &N); 90 HashTable H = CreateHashTable(M); 91 int i; 92 for (i = 0; i < N-1; i++) 93 { 94 int num; 95 scanf("%d", &num); 96 int Pos = Insert(H,num); 97 if (Pos != -1) 98 printf("%d ", Pos); 99 else 100 printf("- "); 101 } 102 int num; 103 scanf("%d", &num); 104 int Pos = Insert(H, num); 105 if (Pos != -1) 106 printf("%d", Pos); 107 else 108 printf("-"); 109 return 0; 110 }
PTA第32题
直白的利用散列的题 直接暴力就可以做 哈希函数可以不做处理

1 #define _CRT_SECURE_NO_WARNINGS 2 #include<stdio.h> 3 #include<malloc.h> 4 #include<math.h> 5 #include<stdlib.h> 6 #include<string.h> 7 #define KEYLENGTH 16 //关键词类型长度 8 #define MAXTABLESIZE 200000 9 10 typedef char ElementType[KEYLENGTH + 1]; 11 typedef int Pos; 12 13 typedef struct LNode* PtrToNode; 14 struct LNode 15 { 16 ElementType QAccount; 17 ElementType QPassWord; 18 PtrToNode Next; 19 }; 20 typedef PtrToNode List; 21 typedef PtrToNode Position; 22 23 typedef struct HblNode* HashTable; 24 struct HblNode 25 { 26 int TableSize; 27 List Heads; 28 }; 29 30 int NextPrime(int N) 31 { 32 int p = (N % 2)?N + 2:N + 1; 33 int i; 34 for (i = (int)sqrt(p); i > 2; i--) 35 { 36 if (p % i == 0) 37 break; 38 if (i == 2)break; 39 else 40 p += 2; 41 } 42 return p; 43 } 44 long Atoi(ElementType Key, int TableSize) 45 { 46 long sum = 0; 47 int length = strlen(Key); 48 for (int i = 0; i < length; i++) 49 sum += sum * 10 + Key[i] - '0'; 50 return sum; 51 } 52 int Hash(ElementType Key,int TableSize) 53 { 54 return atoi(Key) % TableSize; 55 } 56 HashTable CreateHashTable(int TableSize) 57 { 58 HashTable H; 59 H = (HashTable)malloc(sizeof(struct HblNode)); 60 H->TableSize = NextPrime(TableSize); 61 H->Heads = (List)malloc(H->TableSize * sizeof(struct LNode)); 62 for (int i = 0; i < H->TableSize; i++) 63 { 64 H->Heads[i].QAccount[0] = '\0'; 65 H->Heads[i].QPassWord[0] = '\0'; 66 H->Heads[i].Next = NULL; 67 } 68 return H; 69 } 70 Position Find(HashTable H, ElementType Key) 71 { 72 Position P; 73 Pos pos = Hash(Key, H->TableSize); 74 P = H->Heads[pos].Next; 75 while (P && strcmp(P->QAccount, Key)) 76 P = P->Next; 77 return P; 78 } 79 int Insert(HashTable H, ElementType Key, ElementType QPassWord) 80 { 81 Position Tmp; 82 Position P = Find(H, Key); 83 if (!P) 84 { 85 Pos pos = Hash(Key, H->TableSize); 86 Tmp = (Position)malloc(sizeof(struct LNode)); 87 strcpy(Tmp->QAccount, Key); 88 strcpy(Tmp->QPassWord, QPassWord); 89 Tmp->Next = H->Heads[pos].Next; 90 H->Heads[pos].Next = Tmp; 91 return 1; 92 } 93 return 0; 94 } 95 96 void Order_N(HashTable H,char* QAccount,char* QPassWord) 97 { 98 if (Insert(H, QAccount, QPassWord)) 99 printf("New: OK\n"); 100 else 101 printf("ERROR: Exist\n"); 102 103 } 104 void Order_L(HashTable H,char* QAccount, char* QPassWord) 105 { 106 Position P=Find(H,QAccount); 107 if (P) 108 { 109 if (!strcmp(P->QPassWord, QPassWord)) 110 printf("Login: OK\n"); 111 else 112 printf("ERROR: Wrong PW\n"); 113 } 114 else 115 printf("ERROR: Not Exist\n"); 116 117 } 118 int main() 119 { 120 int N; 121 scanf("%d", &N); 122 HashTable H = CreateHashTable(N); 123 for (int i = 0; i < N; i++) 124 { 125 char Choice[2]; 126 char QAccount[11]; 127 char QPassWorld[17]; 128 scanf("\n%s %s %s", Choice, QAccount, QPassWorld); 129 switch (Choice[0]) 130 { 131 case 'N':Order_N(H, QAccount, QPassWorld); break; 132 case 'L':Order_L(H, QAccount, QPassWorld); break; 133 } 134 } 135 return 0; 136 }
至此 数据结构算是入了门(说是如此 但前面学的没复习又忘了 现在至少知道数据结构在讲什么了) 以后要经常刷题 不然根本学不会。。。
(os:一个月前立下的flag算是完成了一半吧 还行)





 浙公网安备 33010602011771号
浙公网安备 33010602011771号