数据结构学习第二十三天

13:50:24 2019-09-14

继续把未看完的看完

13:19:50 2019-09-15

补上了归并的非递归算法

16:10:24 2019-09-17

补上了堆排序的精明版本

排序算法

定理:任意$N$个不同元素组成的序列平均具有$N(N-1)/4$个逆序对

定理:任何仅以交换相邻两元素来排序的算法，其平均时间复杂度为$Ω(N^2)$

这样子冒泡排序插入排序的最坏情况都是 N^2

要使排序算法变高效得使用间隔元素来交换在一次排序中交换多个逆序对的元素

希尔排序

定义增量序列$D_M>D_{M-1}>...>D_1=1$

$对每个D_k进行“D_k-间隔”排序（k=M,M-1,...1)$

$注意：“D_k-间隔"有序的序列，在执行”D_{k-1}间隔“排序后，仍然是“D_k-间隔"有序的$

如果增量元素不互质，则小增量可能根本不起作用

比如 $N=N/2$ 最坏情况时候 $T=\theta(N^{2})$

那么就会有其他的增量序列:

　　Hibbard增量序列 $D_k=2^k-1$ --相邻元素互质最坏情况$T=\theta(N^{3/2})$

　　猜想 Hibbard增量的平均复杂度 $T_{avg}=O(N^{5/4})$

　　Sedgewick增量序列 $ \{1,5,19,41,109,.....\}$

　　$9*4^i-9*2^i或4^i-3*2^i+1$猜想$T_{avg}=O(N^{7/6}) T_{worst}=O(N^{4/3})$

归并排序的时间复杂度为$O(NlogN)$ 该算法是稳定的

冒泡排序插入排序希尔排序选择排序堆排序归并排序(递归与非递归) (ps:其中堆排序写的是憨憨版本之后会添上精明版本)

  1 #define _CRT_SECURE_NO_WARNINGS  
  2 #include<stdio.h>
  3 #include<malloc.h>
  4 void Print(int A[], int N)
  5 {
  6     for (int i = 0; i < N; i++)
  7         printf("%d ", A[i]);
  8     printf("\n");
  9 }
 10 //排序算法
 11 
 12 //冒泡排序   //最好 O(N) 最坏 O(N^2)  算法稳定
 13 void Swap(int A[], int i, int j)
 14 {
 15     int temp = A[i];
 16     A[i] = A[j];
 17     A[j] = temp;
 18 }
 19 void Bubble_Sort(int A[], int N)
 20 {
 21     for (int i = 0; i < N; i++)
 22     {
 23         int IsSwap = 0;
 24         for (int j = 0; j < N - i-1; j++)
 25         {
 26             if (A[j] > A[j + 1])
 27             {
 28                 IsSwap = 1;
 29                 Swap(A, j, j + 1);
 30             }
 31         }
 32         if (!IsSwap)
 33             break;
 34     }
 35 }
 36 
 37 //插入排序  //最好O(N) 最坏 O(N^2)  算法稳定
 38 void Insert(int A[], int j, int i) 
 39 {
 40     int temp = A[i];
 41     for (; i > j; i--)
 42         A[i] = A[i - 1];
 43     A[j] = temp;
 44 }
 45 void Insert_Sort(int A[], int N)
 46 {
 47     /*for (int i = 0; i < N-1; i++)
 48     {
 49         int m = i + 1;
 50         int j = i;
 51         while (j >= 0 && A[j] > A[m])
 52             j--;
 53         Insert(A, j+1, m);
 54     }*/
 55     /*for (int i = 1; i < N; i++)
 56     {
 57         int temp = A[i];
 58         int j;
 59         for (j = i - 1; j >= 0 && A[j] > temp; j--)
 60             A[j + 1] = A[j];
 61         A[j + 1] = temp;
 62     }*/
 63     for (int p = 1; p < N; p++)
 64     {
 65         int temp = A[p];
 66         int i;
 67         for (i = p; i > 0 && A[i - 1] > temp; i--)
 68             A[i] = A[i - 1];
 69         A[i] = temp;
 70     }
 71 }
 72 
 73 //希尔排序  //最坏情况  //改进插入排序
 74 void Shell_Sort(int A[], int N)
 75 {
 76     /*for (int D = N / 2; D > 0; D /= 2)
 77     {
 78         for (int p = D; p < N; p++)
 79         {
 80             int temp = A[p];
 81             int i;
 82             for (i = p; i >= D && A[i - D] > temp; i -= D)
 83                 A[i] = A[i - D];
 84             A[i] = temp;
 85         }
 86     }*/
 87     // 利用Sedgewick增量序列
 88     int Si;
 89     int Sedgewick[] = { 929,505,209,109,41,19,5,1,0 };
 90     for (Si = 0; Sedgewick[Si] >=N; Si++)  //初始的增量Sedgewick[Si]不能超过待排序序列长度
 91         ;
 92     for (int D = Sedgewick[Si]; D>0;D=Sedgewick[++Si])
 93     {
 94         for (int p = D; p < N; p++)
 95         {
 96             int temp = A[p];
 97             int i;
 98             for (i = p; i >= D && A[i - D] > temp; i -= D)
 99                 A[i] = A[i - D];
100             A[i] = temp;
101         }
102     }
103 }
104 
105 //选择排序
106 void Selection_Sort(int A[], int N)
107 {
108     for (int i = 0; i < N; i++)
109     {
110         int MinPosition = i;
111         int Min = A[i];
112         int j;
113         for (j = i + 1; j < N; j++)
114         {
115             if (A[j] < Min)
116             {
117                 MinPosition = j;
118                 Min = A[j];
119             }
120         }
121         Swap(A, i, MinPosition);
122     }
123 }
124 
125 //堆排序  //选择排序的一种改进
126 //改进了寻找最小元的算法 利用最小堆来实现
127 typedef struct HeapStruct* MinHeap;
128 struct HeapStruct
129 {
130     int* Elements;
131     int Size;
132     int Capacity;
133 };
134 MinHeap Create(int MaxSize)
135 {
136     MinHeap H = (MinHeap)malloc(sizeof(struct HeapStruct));
137     H->Elements = (int*)malloc(sizeof(int) * (MaxSize + 1));
138     H->Capacity = MaxSize;
139     H->Size = 0;
140     H->Elements[0] = -10001;
141     return H;
142 }
143 MinHeap H = Create(20);
144 //建立最小堆
145 void PrecDown(MinHeap H, int i)  //下滤
146 {
147     int Parent, Child;
148     int Tmp = H->Elements[i];
149     for (Parent = i; Parent * 2 <= H->Size; Parent = Child)
150     {
151         Child = Parent * 2;
152         if ((Child != H->Size) && (H->Elements[Child] > H->Elements[Child + 1]))
153             Child++;
154         if (Tmp <= H->Elements[Child])break;
155         else
156             H->Elements[Parent] = H->Elements[Child];
157     }
158     H->Elements[Parent] = Tmp;
159 }
160 void BuildMinHeap(MinHeap H)
161 {
162     int i;
163     for (i = H->Size / 2; i > 0; i--)
164         PrecDown(H, i);
165 }
166 int DeleteMin(MinHeap H)
167 {
168     int Parent, Child;
169     int MinItem, temp;
170     MinItem = H->Elements[1];
171     temp = H->Elements[H->Size--];
172     for (Parent = 1; Parent * 2 <= H->Size; Parent = Child)
173     {
174         Child = Parent * 2;
175         if (Child != H->Size && H->Elements[Child] > H->Elements[Child + 1])
176             Child++;
177         if (H->Elements[Child] >= temp)break;
178         else
179             H->Elements[Parent] = H->Elements[Child];
180     }
181     H->Elements[Parent] = temp;
182     return MinItem;
183 }
184 
185 //利用最大堆实现堆排序 (升序)
186 void Precdown(int A[], int i, int N)
187 {
188     int Parent, Child;
189     int Tmp;
190     Tmp = A[i];
191     for (Parent = i; (Parent * 2) + 1 <= N; Parent = Child)
192     {
193         Child = (Parent * 2) + 1;
194         if (Child != N && A[Child] < A[Child + 1])
195             Child++;
196         if (A[Child]<=Tmp)break;
197         else
198             A[Parent] = A[Child];
199     }
200     A[Parent] = Tmp;
201 }
202 void BuildMaxHeap(int A[], int N)
203 {
204     for (int i = (N - 1) / 2; i >= 0; i--)
205         Precdown(A, i, N - 1);
206 }
207 
208 void Heap_Sort(int A[], int N)   
209 {
210     //算法一 利用最小堆
211     /*int Tmp[10] = { 0 };
212     for (int i = 0; i < 10; i++)
213         Tmp[i] = DeleteMin(H);
214     for (int i = 0; i < 10; i++)
215         A[i] = Tmp[i];*/
216 
217     /*for (int i = 0; i < 10; i++)
218         A[i] = DeleteMin(H);*/
219     //算法二 利用最大堆后 再调整
220     BuildMaxHeap(A, N);
221     //之后调整最大堆
222     for (int i = N - 1; i >= 0; i--)
223     {
224         Swap(A, 0, i);
225         Precdown(A, 0, i - 1);
226     }
227 }
228 
229 //归并排序
230 //递归算法
231 void Merge(int A[],int lo,int mi,int hi)
232 {
233     //两个有序序列的合并
234     int* B = (int*)malloc(sizeof(int) * (mi - lo));
235     for (int i = 0; i < mi - lo;i++)B[i] = A[lo + i];
236     int i, j, k; 
237     i = lo;
238     j = 0;
239     k = mi;
240     /*while (j<mi-lo||k<hi)
241     {
242         if((j<mi-lo)&&(k>=hi||B[j]<=A[k]))A[i++]=B[j++];
243         if ((k < hi) && (j >= mi-lo|| B[j] > A[k]))A[i++] = A[k++];
244     }*/
245     //化简版
246     while (j<mi-lo)
247     {
248         if (k >= hi || B[j] <= A[k])A[i++] = B[j++];
249         if (k<hi && B[j]>A[k])A[i++] = A[k++];
250     }
251     /*邓公版本*/
252     /*int* A1= A + lo;
253     int* B = (int*)malloc(sizeof(int) * (mi - lo));
254     for (int i = 0; i < mi - lo; B[i] = A1[i++]);
255     int* C = A + mi;
256     int i, j, k;
257     for (i = j = k = 0; j < mi - lo || k < hi-mi;)
258     {
259         if (j < mi - lo&&((k >= hi - mi)||B[j] <=C[k]))A1[i++] = B[j++];
260         if (k < hi - mi && (j >= mi - lo || B[j] > C[k]))A1[i++] = C[k++];
261     }*/
262     //简化
263     /*for (i = j = k = 0; j < mi - lo;)
264     {
265         if (k >= hi - mi || B[j] <= C[k])A1[i++] = B[j++];
266         if (k < hi - mi && (j >= mi - lo || B[j] > C[k]))A1[i++] = C[k++];
267     }*/
268     free(B);
269 }
270 void MergeSort(int A[],int lo,int hi)
271 {
272     if (lo == hi - 1)
273         return;
274     int mi = (lo + hi) >> 1;
275     MergeSort(A,lo, mi);
276     MergeSort(A, mi, hi);
277     Merge(A,lo, mi, hi);
278 }
279 //非递归算法
280 void Merge_pass(int A[],int N, int length) //length为当前有序子列的长度
281 {
282     int i;
283     for (i = 0; i <= N - 2 * length;i += 2 * length)
284         Merge(A,i, i + length, i + 2 * length);
285     if (i+length< N)    //如果最后有两个子列
286         Merge(A, i, i+length, N);  
287 }
288 void Merge_Sort(int A[], int N)
289 {
290     int length = 1;
291     while (length<=N)
292     {
293         Merge_pass(A, N, length);
294         length *= 2;
295     }
296 }
297 
298 int main() 
299 {
300     int A[10];
301     for (int i = 0; i < 10; i++)
302         scanf("%d", &A[i]);
303     //Bubble_Sort(A, 10);    //冒泡排序
304     //Insert_Sort(A, 10);    //插入排序
305     //Shell_Sort(A, 10);    //希尔排序
306     //Selection_Sort(A, 10);    //选择排序
307 
308     //堆排序   //最小堆之憨憨算法
309     /*for (int i = 1; i <= 10; i++)
310         H->Elements[++H->Size] = A[i - 1];
311     BuildMinHeap(H);   //构建最小堆
312     Heap_Sort(A, 10);*/
313 
314     //堆排序  //最大堆之精比算法
315     Heap_Sort(A, 10);
316 
317     //MergeSort(A,0,10) //归并排序递归算法
318     //Merge_Sort(A,10);    //归并排序非递归算法
319     Print(A, 10);
320     return 0;
321 }

View Code

快速排序:是排序算法中最快的但要注意实现的细节(对于大规模数据来说)

首先要注意主元的选取对主元的选取会影响到算法的时间复杂度还有就是快速排序是利用递归实现的对于小规模数据可能整体时间不入插入排序快因此可以使用一个$Cutoff$ 当数据规模过小时不使用快排而使用插入排序

下面会给出对快速排序的测试

表排序

不移动元素本身而移动指针的排序叫做间接排序

利用一个Table数组来对下标进行排序

物理排序

　　N个数字的排列由若干个独立的环组成

桶排序

基数排序

　　用“次位优先" (Least Significant Digit)

　　"主位优先"(Most Significant Digit)

对排序的测试

冒泡排序: 可以看出当数据量过大时运行超时

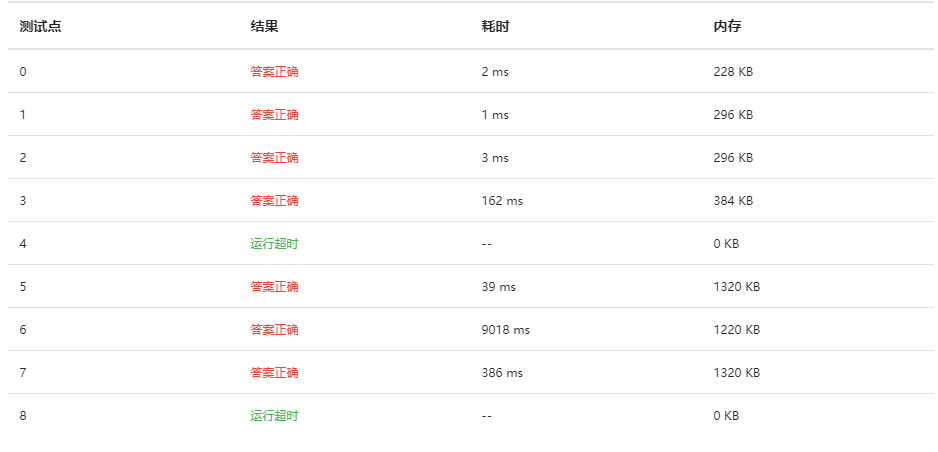
插入排序:虽然所有数据都能排序，但当数据量过大时，耗时增加

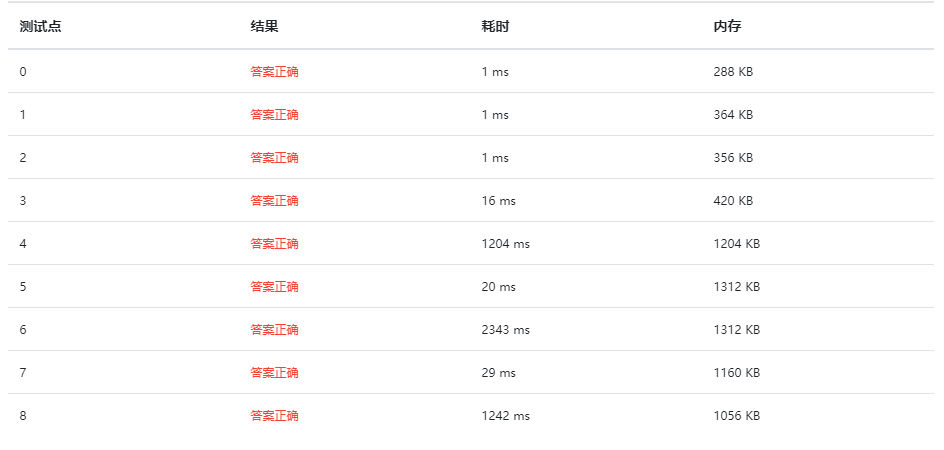
希尔排序(Sedgewick):希尔排序快了不少

选择排序:答案正确,耗时却不少

堆排序(憨憨版本):速度也很快

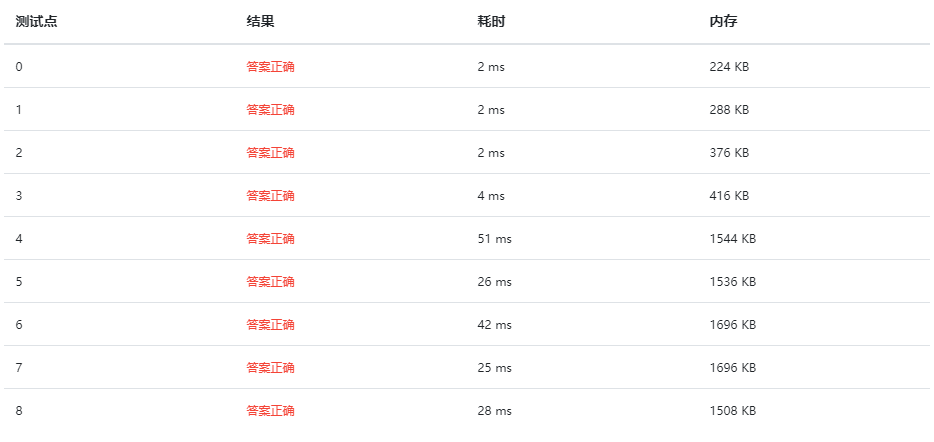
堆排序(精明版本): 速度也挺好

归并排序(递归)：也很快但占的内存却很大比前面的排序大了4、5倍经检查是因为没有在归并算法里free掉申请的空间

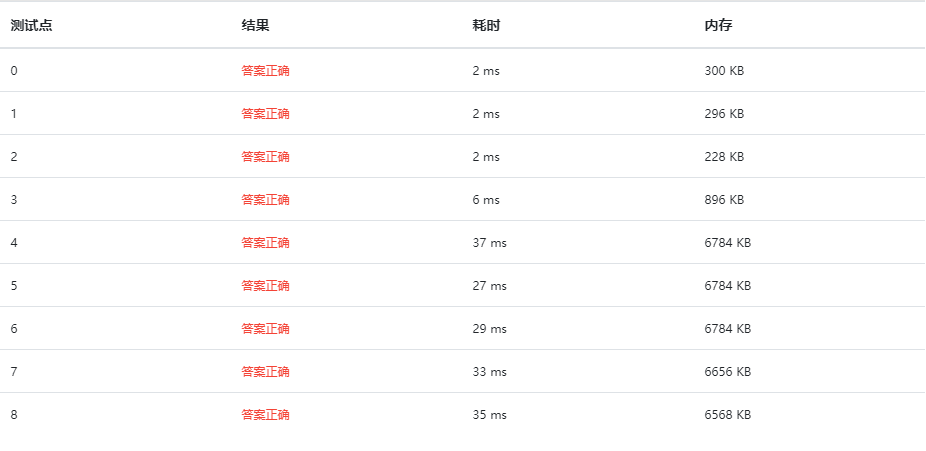
每次申请完空间后释放掉内存占用就少了许多

归并排序(非递归) :看起来内存占用并没有少一方面是因为我没有用陈越姥姥的方法去写递归与非递归的排序更重要的是开辟的数组空间很大但也可以看出非递归算法比递归快一些

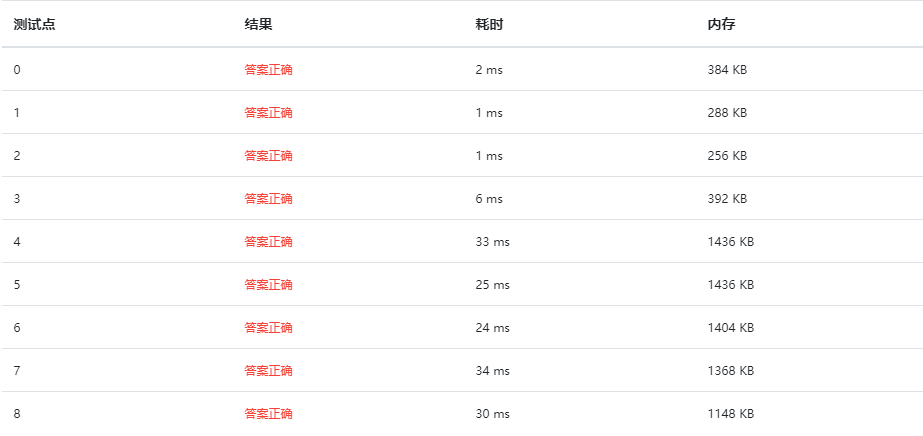
对快速排序的测试:

对pivot进行测试(此时不使用Cutoff来限定范围)：

①pivot采取A[0] 有三个数据点耗时较多

②pivot采取A[mi] 速度不错

③pivot采取三元选中值某个数据点慢了些其他都挺快的

④采用随机函数rand() 速度也行不知道改一改获取rand值的函数会不会更快点

对Cutoff进行测试(此时选取pivot为A[mi]):

①Cutoff取值为50

②Cutoff取100

③Cutoff取200

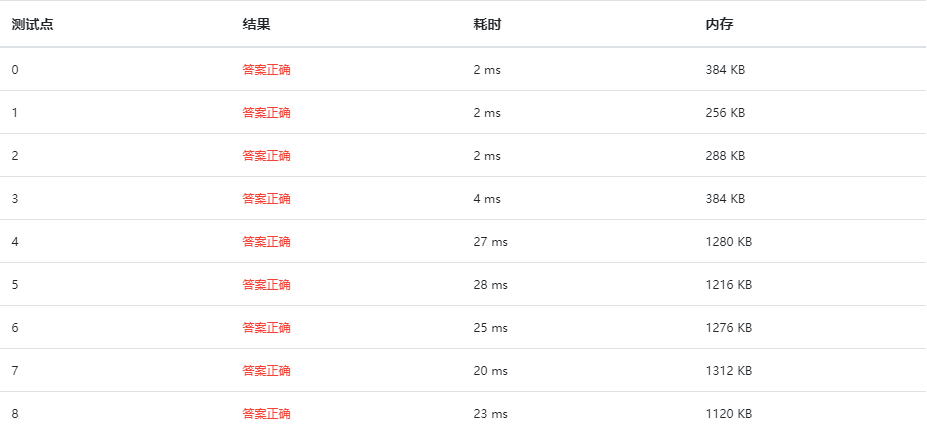
④Cutoff取300

⑤Cutoff取400

PTA第27题简单的一道桶排序题

 1 #define _CRT_SECURE_NO_WARNINGS  
 2 #include<stdio.h>
 3 #include<malloc.h>
 4 #include<stdlib.h>
 5 int Bucket[55];
 6 int main()
 7 {
 8     int N,Num;
 9     scanf("%d", &N);
10     for (int i = 0; i < N; i++)
11     {
12         scanf("%d", &Num);
13         Bucket[Num]++;
14     }
15     int count = 0;
16     for (int i = 0; i < 55; i++)
17     {
18         if (Bucket[i])
19         {
20             printf("%d:%d\n", i, Bucket[i]);
21             count++;
22         }
23     }
24 }

View Code

PTA 第25题根据给的2串数组判断是插入排序还是归并排序

我是用归并的想法不断检查以Length为长度的数组判断是否满足是归并的最小条件(Length=2时满足)

如果满足就继续向下查更新之后需要的长度L 不是就返回去做下一步操作

(os:这是PTA 2014年冬季考试题...我做了有一个小时四十分钟。。这还不算昨天思考的时间。。这要去考试不得凉凉)

  1 #define _CRT_SECURE_NO_WARNINGS  
  2 #include<stdio.h>
  3 #include<malloc.h>
  4 #include<stdlib.h>
  5 int A[110];
  6 int B[110];
  7 int L;
  8 void Print(int N)
  9 {
 10     int i;
 11     for (i = 0; i < N - 1; i++)
 12         printf("%d ", B[i]);
 13     printf("%d", B[i]);
 14 }
 15 int IsOrder(int B[],int lo, int hi)
 16 {
 17     for (int i = lo; i < hi - 1; i++)
 18         if (B[i] > B[i + 1])
 19             return 0;
 20     return 1;
 21 }
 22 int ChargeLength(int B[], int N, int Length)  //检查以Length为长度的序列
 23 {
 24     int i;
 25     for (i = 0; i < N -Length; i +=Length)
 26         if (!IsOrder(B, i, i+Length))
 27             return 0;
 28     if (i< N)
 29         if (!IsOrder(B, i, N))
 30             return 0;
 31     L = Length;
 32     return 1;
 33 }
 34 int Charge(int B[], int N)
 35 {
 36     int Length = 2;
 37     while(Length <=N)
 38     {
 39         if (ChargeLength(B, N, Length))
 40             Length *= 2;
 41         else
 42             if (Length > 2)
 43                 return 1;
 44             else
 45                 return 0;
 46     }
 47 }
 48 
 49 void Insert_Once(int B[],int i,int N)
 50 {
 51     int j;
 52     int Temp = B[i];
 53     for (j = i; j > 0 && B[j - 1] >Temp; j--)
 54         B[j] = B[j - 1];
 55     B[j] = Temp;
 56 }
 57 
 58 void Merge(int lo, int mi, int hi)
 59 {
 60     int* B1 = (int*)malloc(sizeof(int) * (mi - lo));
 61     for (int i = 0; i < mi - lo; i++)B1[i] = B[lo + i];
 62     int i, j, k;
 63     i = lo;
 64     j = 0;
 65     k = mi;
 66     while (j < mi - lo)
 67     {
 68         if (k >= hi || B1[j] <= B[k])B[i++] = B1[j++];
 69         if (k<hi && B1[j]>B[k])B[i++] = B[k++];
 70     }
 71     free(B1);
 72 }
 73 void Merge_Once(int B[], int Length, int N)
 74 {
 75     int i;
 76     for (i = 0; i < N - 2 * Length; i += 2 * Length)
 77         Merge(i, i + Length, i + 2 * Length);
 78     if (i + Length < N)
 79         Merge(i, i + Length, N);
 80 }
 81 
 82 int main()
 83 {
 84     int N;
 85     int Flag = 0;
 86     int OrderPosition = 0;
 87     scanf("%d", &N);
 88     for (int i = 0; i < N; i++)
 89         scanf("%d", &A[i]);
 90     for (int i = 0; i < N; i++)
 91         scanf("%d", &B[i]);
 92     if (Flag=Charge(B, N))
 93         printf("Merge Sort\n");
 94     else
 95         printf("Insertion Sort\n");
 96     for (int i = 0; i < N - 1; i++)
 97         if (B[i] <=B[i + 1])     //这里必须是大于等于
 98             OrderPosition = i + 1;
 99         else
100             break;
101     if (Flag)
102         Merge_Once(B, L, N);
103     else
104         Insert_Once(B, OrderPosition+1, N);
105     Print(N);
106     return 0;
107 }

View Code

PTA 第26题根据给的两串数组判断是插入排序还是堆排序

观察数据可以发现是利用精明算法来实现堆排序

判断是堆排序还是插入排序我是直接看前三个元素

这道题给出的例子至少会经过一次排序所以看前三个元素就可以知道是什么排序了简单来说插入排序最早就把前两个元素排好序了而堆排序对前两个元素的排序是最后才排的

至于接下来做一步操作插入排序很简单堆排序我是直接把排序好的结果与给的数据进行比较来找出那个位置点

  1 #define _CRT_SECURE_NO_WARNINGS  
  2 #include<stdio.h>
  3 #include<malloc.h>
  4 #include<stdlib.h>
  5 int A[110];
  6 int B[110];
  7 int L;
  8 void Swap(int *C,int i, int j)
  9 {
 10     int temp = C[i];
 11     C[i] = C[j];
 12     C[j] = temp;
 13 }
 14 
 15 void Print(int N)
 16 {
 17     int i;
 18     for (i = 0; i < N - 1; i++)
 19         printf("%d ", B[i]);
 20     printf("%d", B[i]);
 21 }
 22 
 23 int Charge(int N)
 24 {
 25     int i;
 26     if (B[0] > B[1] && B[0] > B[2])
 27         return 1;
 28     else
 29         return 0;
 30 }
 31 
 32 void Insert_Once(int i, int N)
 33 {
 34     int j;
 35     int Temp = B[i];
 36     for (j = i; j > 0 && B[j - 1] > Temp; j--)
 37         B[j] = B[j - 1];
 38     B[j] = Temp;
 39 }
 40 
 41 void PrecDown(int i,int N)
 42 {
 43     int Parent, Child;
 44     int Tmp = A[i];
 45     for (Parent = i; Parent * 2 + 1 <= N; Parent = Child)
 46     {
 47         Child = Parent * 2 + 1;
 48         if (Child != N && A[Child] < A[Child + 1])
 49             Child++;
 50         if (Tmp >= A[Child])break;
 51         else
 52             A[Parent] = A[Child];
 53     }
 54     A[Parent] = Tmp;
 55 }
 56 
 57 void BuildMaxHeap(int N)
 58 {
 59     for (int i = (N - 1) / 2; i >= 0; i--)
 60         PrecDown(i, N - 1);
 61 }
 62 
 63 void Heap_Sort(int N)
 64 {
 65     for (int i = N - 1; i >= 0; i--)
 66     {
 67         Swap(A, 0, i);
 68         PrecDown(0, i-1);
 69     }
 70 }
 71 
 72 int FindI(int N)
 73 {
 74     int i;
 75     for (i = N - 1; i >= 0 && A[i] == B[i]; i--);
 76     return i;
 77 }
 78 
 79 void PrecDown_Once(int i)
 80 {
 81     Swap(B,0, i);
 82     int Parent, Child;
 83     int tmp;
 84     tmp = B[0];
 85     for (Parent = 0; (Parent * 2) + 1 <= i-1; Parent = Child)
 86     {
 87         Child = (Parent * 2) + 1;
 88         if (Child != i-1&& B[Child]<B[Child + 1])
 89             Child++;
 90         if (tmp >= B[Child])break;
 91         else
 92             B[Parent] = B[Child];
 93     }
 94     B[Parent] = tmp;
 95 }
 96 
 97 void Heap_Once(int N)
 98 {
 99     BuildMaxHeap(N);
100     Heap_Sort(N);
101     int i = FindI(N);
102     PrecDown_Once(i);
103 }
104 
105 int main()
106 {
107     int N;
108     int Flag = 0;
109     int OrderPosition = 0;
110     scanf("%d", &N);
111     for (int i = 0; i < N; i++)
112         scanf("%d", &A[i]);
113     for (int i = 0; i < N; i++)
114         scanf("%d", &B[i]);
115     if (Flag = Charge(N))
116         printf("Heap Sort\n");
117     else
118         printf("Insertion Sort\n");
119     for (int i = 0; i < N - 1; i++)
120         if (B[i] <= B[i + 1])     //这里必须是大于等于
121             OrderPosition = i + 1;
122         else
123             break;
124     if (Flag)
125         Heap_Once(N);
126     else
127         Insert_Once(OrderPosition + 1, N);
128     Print(N);
129     return 0;
130 }

View Code

posted @ 2019-09-14 17:54 57one 阅读(201) 评论(0) 编辑收藏举报

刷新页面返回顶部

57one

数据结构学习第二十三天

公告