数据结构学习第十一天

10:15:16 2019-08-26

学习

 22:43:02 2019-08-26

从树开始 打算去 看另一个教程了。。。=，=(博主发现自己果真是个憨憨)

栈的应用：

逆序输出:进制转化

递归嵌套:括号匹配

延迟缓冲:中缀表达式求值

 下面是用 数组digit 来对余数进行修改 //满足超过10进制的需求

 

栈混洗数:

$sp(n)=\sum_{k=1}^n[sp(k-1)*sp(n-k)]$

这个就是卡特兰数

卡特兰数：

$f(n)=\frac{{C}\binom{n}{2n}}{n+1}=\frac{2n!}{(n+1)!n!}$

 

若k要在三个元素之前 前面的i j会以固定的顺序被压入中转栈 S 之后 也会以固定的顺序从 中转栈中弹出并压入结果栈中 即只要k在前 他们之间的相对顺序是固定的 不可能出现 k i j的情况(应是 k j i)

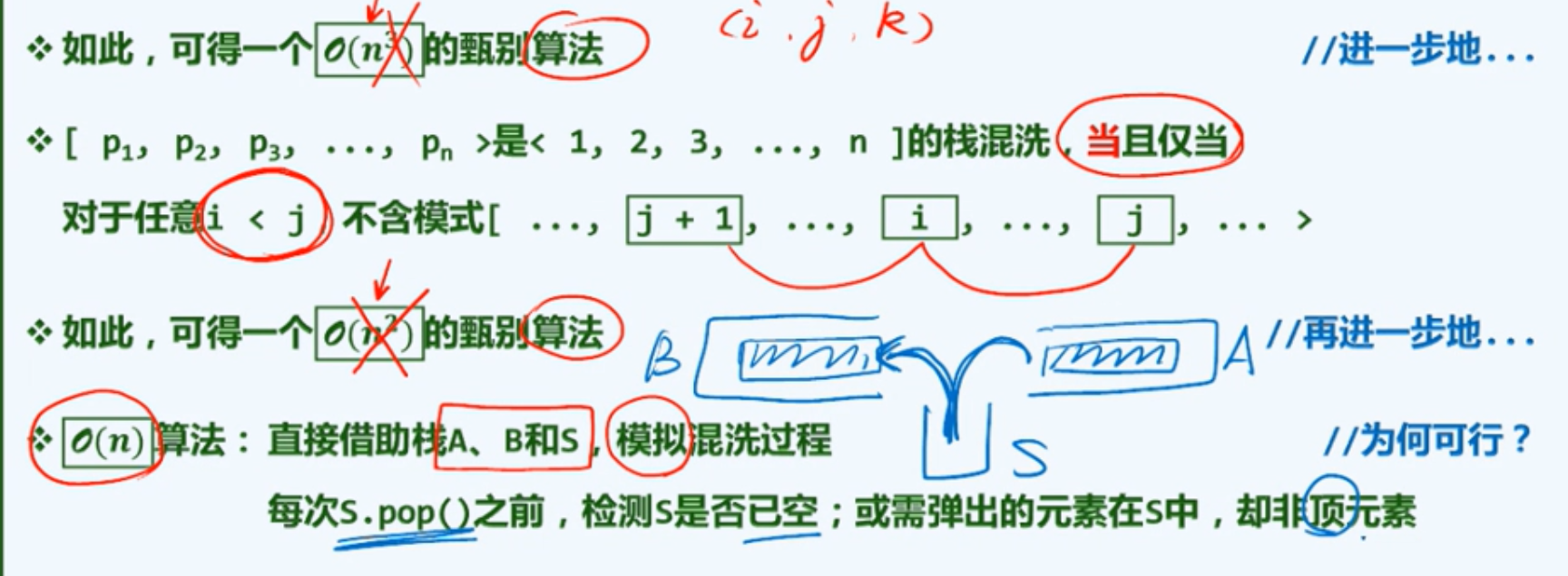
邓公讲的 栈应用(未完全实现)

  1 #define _CRT_SECURE_NO_WARNINGS    //vs中scanf为不安全的函数 要使用 得加上这句话
  2 #include<stdio.h>
  3 #include<malloc.h>
  4 #define Size 10
  5 int Vector[Size];
  6 int size;
  7 //栈与队列
  8 void Insert(int Rank, int Element) //按秩插入元素
  9 {
 10     if (Rank < Size)
 11     {
 12         for (int i = Size - 1; i > Rank; i--)
 13         {
 14             Vector[i] = Vector[i - 1];
 15         }
 16         Vector[Rank] = Element;
 17         size++;
 18     }
 19 }
 20 int Delete(int lo, int hi)  //区间删除 单元素删除时区间删除的特列
 21 {
 22     for (; hi < size;)
 23         Vector[lo++] = Vector[hi++];
 24     size -= hi - lo;
 25     return hi - lo;
 26 }
 27 int Find(int Element, int lo, int hi)  //在范围中查找元素
 28 {
 29     while (lo < hi-- && Vector[hi] != Element);
 30     return hi;
 31 }
 32 int  DeleteOne(int Rank)   //单元素删除
 33 {
 34     int Element = Vector[Rank];
 35     Delete(Rank, Rank + 1);
 36     return Element;
 37 }
 38 void Push(int Element)
 39 {
 40     Insert(size, Element);
 41 }
 42 int Pop()
 43 {
 44     return DeleteOne(size - 1);
 45 }
 46 int Top()
 47 {
 48     return Vector[size - 1];
 49 }
 50 int Empty()    //空返回非0值   非空返回0值
 51 {
 52     return !size;
 53 }
 54 
 55 //栈应用
 56 
 57 //逆序输出  
 58 //例子 进制转换
 59 void Convert(int Num,int n)        //如果超出10进制 就不能用整型向量来接受了(os:从这也能看出c++的优点)
 60 {                                //需要使用一个Digit数组对计算出的余数进行转换
 61     /*if (Num == 0)
 62         return; 
 63     Vector[size++] = Num%n;   //写了接口 没用到 谨记
 64     Convert(Num / n, n);*/ 
 65     //迭代版本
 66     while (Num>0)
 67     {
 68         Push(Num % n);
 69         Num /= n;
 70     }
 71 }
 72 
 73 //括号匹配
 74 char Match(char LeftOp)      //匹配转换 比较
 75 {
 76     if (LeftOp == '(')
 77         return ')';
 78     else if (LeftOp == '[')
 79         return ']';
 80     else
 81         return '}';
 82 }
 83 int paren(char exp[],int lo,int hi)   //返回1 匹配成功   返回0 匹配失败
 84 {
 85     /*for (int i = lo; i < hi; i++)
 86     {
 87         if (exp[i] == '(')   //左括号 压入
 88             Push(exp[i]);
 89         else if (!Empty())      //遇到右括号且栈不为空 弹出
 90             Pop();
 91         else
 92             return !Empty();    //栈为空 匹配失败
 93     }
 94     return Empty();    //最终 栈为空 不为空 匹配失败*/
 95     // 拓展到多种括号的情况
 96     for (int i = lo; i < hi; i++)
 97     {
 98         if (exp[i] == '(' || exp[i] == '[' || exp[i] == '{')
 99             Push(exp[i]);
100         else if (!Empty())    //遇到右括号 先判断非空
101         {
102             if (Match(Top()) == exp[i])    //匹配成功 弹出
103                 Pop();
104             else
105                 return 0;            //匹配失败
106         }
107         else
108             return !Empty();
109     }
110     return Empty();   //如果成功 栈一定为空
111 }
112 
113 int main()
114 {
115     /*int num=0, n=0;    
116     scanf("%d", &num);
117     scanf("%d", &n);
118     Convert(num, n);                
119     while (!Empty())                //因为接口写的不好 在里面对Size进行了修改
120     {
121         printf("%d", Pop());    
122     }*/                            //进制转换
123 
124 }
View Code

树的接口

 

posted @ 2019-08-26 22:55  57one  阅读(142)  评论(0)  编辑  收藏  举报