排序算法总结

1、冒泡排序

     

//冒泡排序
      void bubbleSort(int A[], int n)
      {
          bool flag = false;
          for (int i = n - 1; i > 0; i--)
          {
              //注意i,j的终止条件
              for (int j = 0; j < i; j++)
              {
                  if (A[j]>A[j + 1])swap(A[j], A[j + 1]);
                  flag = true;
              }

              if (flag == false)return;
          }

      }

    （上面代码有误，交换和改变flag值应有大括号）

最差时间复杂度 O(n²) 记录是反序的，需要n-1次扫描，每趟扫描进行n-i次比较，每次比较都要移动3次

最优时间复杂度 O(n) 记录是正序的，一趟扫描即可完成，比较n-1次

平均时间复杂度 O(n²)

虽然冒泡排序不一定进行n-1趟，但记录移动次数多，故平均时间性能比直接插入排序差

最差空间复杂度 O(1)

优点：稳定；

缺点：慢，每次只能移动相邻两个数据

 

2、插入排序

     

//插入排序
      void insertSort(int A[], int n)
      {
          for (int i = 1; i < n; i++)
          {
              //注意j从i-1开始
              for (int j = i - 1; j >= 0;j--)
              if (A[i] < A[j])
                  swap(A[i], A[j]);
          }
      }

 

 

最差时间复杂度 O(n²)最优时间复杂度 O(n)平均时间复杂度 O(n²)最差空间复杂度 O(n) total, O(1) auxiliary

 

3、希尔排序

 

//希尔排序
      void shellSort(int A[], int n)
      {
          int incrment = n;
          do{
              incrment = n / 3 + 1;
              shellPass(A, n, incrment);
          } while (n >= 1);
      }
      void shellPass(int A[], int n, int d)
      {
          for (int i = d; i < n;i++)
          for (int j = i - d; j >= 0 && A[j]>A[i]; j -= d)//注意j每次自减d，A[j]>A[i]放在判断条件效率更高
          {
              swap(A[i], A[j]);
          }
      }

希尔排序实际上是一种插入排序, 它的时间复杂度和数组初始排序有关。

平均时间复杂度：O(nlogn)

空间复杂度：O(1)

优点：快，数据移动少；

缺点：不稳定，d的取值是多少，应取多少个不同的值，都无法确切知道，只能凭经验来取。

 4、选择排序

 

//选择排序
      void selectSort(int A[], int n)
      {
          for (int i = 0; i < n - 1;i++)
          for (int j = i + 1; j < n; j++)
          {
              if (A[i]>A[j])
                  swap(A[i], A[j]);
          }
      }

 

和冒泡排序的思想类似。

最差时间复杂度 О(n²)最优时间复杂度 О(n²)平均时间复杂度 О(n²)最差空间复杂度 О(n) total, O(1) auxiliary

5、归并排序

//归并排序

      void merge(int A[], int first, int mid, int last, int temp[])
      {
          int i = first, j = mid + 1;
          int m = mid, int n = last;
          int k = 0;
          while (i <= m&&j <= n)
          {
              if (A[i] < A[j])
                  temp[k++] = A[i++];
              else
                  temp[k++] = A[j++];
          }

          while (i <= m)
              temp[k++] = A[i++];

          while (j <= n)
              temp[k++] = A[j++];

          for (i = 0; i < k; i++)//注意起始位置
              A[first + i] = temp[k++];
      }

      void mSort(int A[], int first, int last, int temp[])
      {
          int mid = (first + last) / 2;
          mSort(A, first, mid, temp);
          mSort(A, mid + 1, last, temp);

          merge(A, first, mid, last, temp);
      }

      bool mergeSort(int A[], int n)
      {
          //统一接口，只在开始声明数组，提高效率
          int *p = new int[n];
          if (p == nullptr)return false;
          mSort(A, 0, n - 1, p);
          delete[] p;
          return true;
      }

 

平均时间复杂度：O(nlogn)，效率较高

6、堆排序

堆排序包含两个过程:

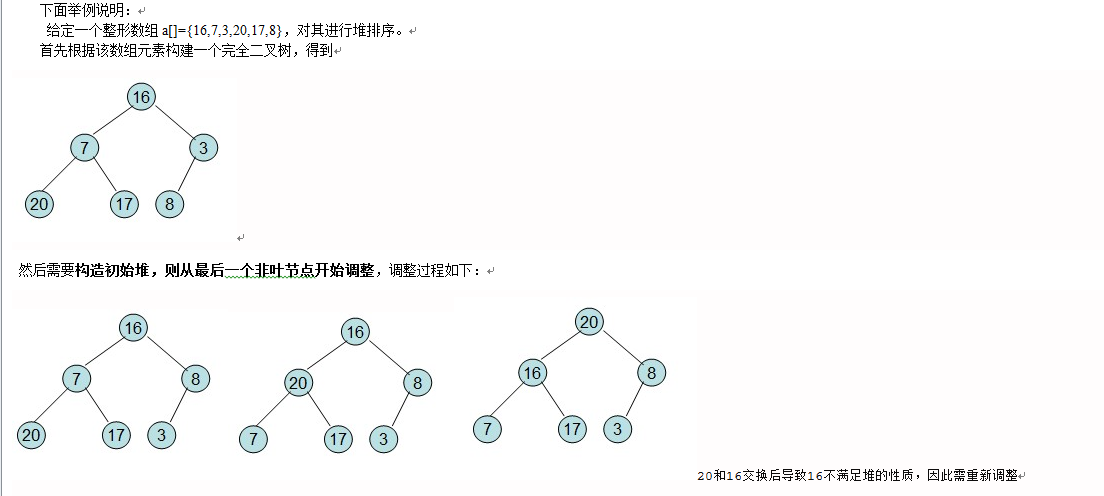
(1)初建堆

(2)调整堆

初建堆:从非终端结点开始一直到根结点,执行调整堆的过程。这样,就会建立一个大顶堆。

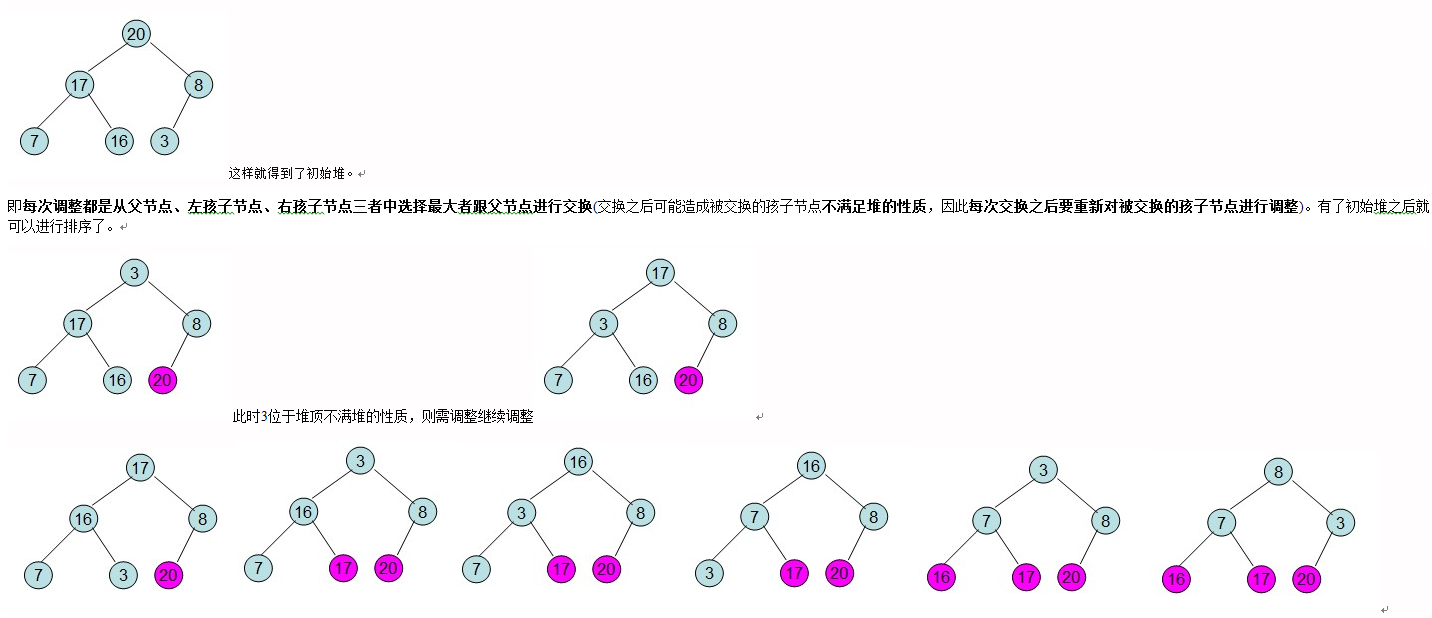
调整堆:对于第二个过程,描述如下,第一次,取出堆顶元素与R[n]进行交换,然后从根结点开始调整堆,根结点与左右孩子中较大者交换,这样，

左右子树的堆会被破坏,继续进行上述操作,直到叶子结点为止。第二次,取出堆顶元素与R[n-1]交换,然后调整堆。

如果排序过程中,是按照从小到大正序,那么建立一个大顶堆。如果是逆序就建立一个小顶堆。

 

 //堆排序

      void adjustHeap(int A[], int i, int n)
      {
          //调整为最大堆
          int temp = A[i];
          for (int j = 2 * i + 1; j < n; j=2*j+1)
          {
              //在子结点中找最大的
              if (j + 1 < n&&A[j + 1] > A[j])
                  j++;
              //如果已经是最大，无需调整
              if (temp >= A[j])break;
              //把较大值往上移
              A[i] = A[j];
              i = j;//调整i
          }
          A[i] = temp;
      }

      void heapSort(int A[], int n)
      {
          //建最大堆
          //从最后一个非叶子结点开始调整，分别调整成最大堆
          for (int i = (n - 1) / 2; i >= 0; i--)
              adjustHeap(A, i, n);

          //排序 
          for (int i = n - 1; i >= 0; i--)
          {
              swap(A[0], A[n - 1]);
              //对剩下n-1个结点进行调整
              adjustHeap(A, 0, n - 1);
          }
      }

 

7、快速排序

 

它采用了分治的思想：先保证列表的前半部分都小于后半部分，然后分别对前半部分和后半部分排序，这样整个列表就有序了。快速排序的基本算法是：
1. 从数列中挑出一个元素，称为 "基准"（pivot），
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分割之后，该基准是它的最后位置。这个称为分割（partition）操作。
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。递回的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递回下去，但是这个算法总会结束，

因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

具体做法：

（1）初始化，设置两个指针ij,初值为区间的上下界，即i=low, j=high；选择无序区的第一个记录R[i]作为基准记录，并将它保存在变量pivot中。

（2）另j从high起向左扫描，直到找到第1个关键字小于pivot.key的记录R[j].将R[j]与基准R[i]交换，是关键字小于pivot.key的记录都移到基准的左边，交换后R[j]中是pivot;然后，令i自i+1位置开始向右扫描，

直到找到第1个关键字大于pivot.key的记录R[i]，将R[i]与R[j]交换，交换后，R[i]中存的是pivot,将关键字大于pivot.key的都移动到基准的右边;接着继续扫描，两端往中间靠拢，直到i=j，i就为pivot最终位置。

 

快速排序的时间复杂度是O(nlogn)，

最坏情况下时间复杂度是O(n²)。

平均时间复杂度 Θ(nlogn)

最好的情况是枢纽元选取得当，每次都能均匀的划分序列。 时间复杂度O(nlogn)
最坏情况是枢纽元为最大或者最小数字，那么所有数都划分到一个序列去了，即为有序的情况 时间复杂度为O(n^2)

就空间复杂度来说，主要是递归造成的栈空间的使用，最好情况，递归树的深度为log2n，其空间复杂度也就为O(logn)，最坏情况，需要进行n‐1递归调用，其空间复杂度为O(n)，平均情况，空间复杂度也为O(logn)。

优点： 快速，数据移动少

缺点：不稳定

快速排序被认为是目前基于比较的内部排序中较好的方法，当待排序的关键字随机分布时，快速排序的平均时间最短。

 

堆排序所需的辅助空间少于快速排序，并且不会出现快速排序可能出现的最坏情况，但这两种排序都是不稳定的，归并排序是稳定的。

//快速排序


      int median3(int A[], int left, int right)
      {
          //取主元：取首个，中间，最后元素的中位数
          int mid = (left + right) / 2;
          if (A[left] > A[mid])swap(&A[left], &A[mid]);
          if (A[left] > A[right-1])swap(&A[left], &A[right-1]);
          if (A[mid] > A[right-1])swap(&A[mid], &A[right-1]);
          //同时将主元藏在倒数第二个位置上，只需考虑个[left+1,right-3];
          swap(&A[mid], &A[right - 2]);
          return A[right - 2];
      }

      void quick_sort(int A[], int left, int right)
      {
          int pivot = median3(A, left, right);

          int i = left, j = right - 2;
          for (;;)
          {
              while (A[++i] < pivot);
              while (A[--j] > pivot);

              if (i < j)swap(&A[i], &A[j]);
              else break;
          }

          swap(&A[i], &A[right - 2]);//将pivot交换至正确位置
          quick_sort(A, left, i - 1);
          quick_sort(A, i + 1, right);

      }

      void quickSort(int A[], int n)
      {
          quick_sort(A, 0, n);
      }

 

void quick_sort(vector<int>& a, int start, int end)
{
	if (a.size() == 0 || end - start <= 1 || start < 0)
		return;

	int pivot_pos = start;
	int pivot = a[start];
	int temp;

	for (int i = start + 1; i < end; i++)
	{
		if (a[i] < pivot)
		{
			if (++pivot_pos != i)
			{
				swap(a[pivot_pos], a[i]);
			}
		}
	}
	a[start] = a[pivot_pos];
	a[pivot_pos] = pivot;
	quick_sort(a, start, pivot_pos - 1);
	quick_sort(a, pivot_pos + 1, end);

}