Leetcode 之Largest Rectangle in Histogram（40）

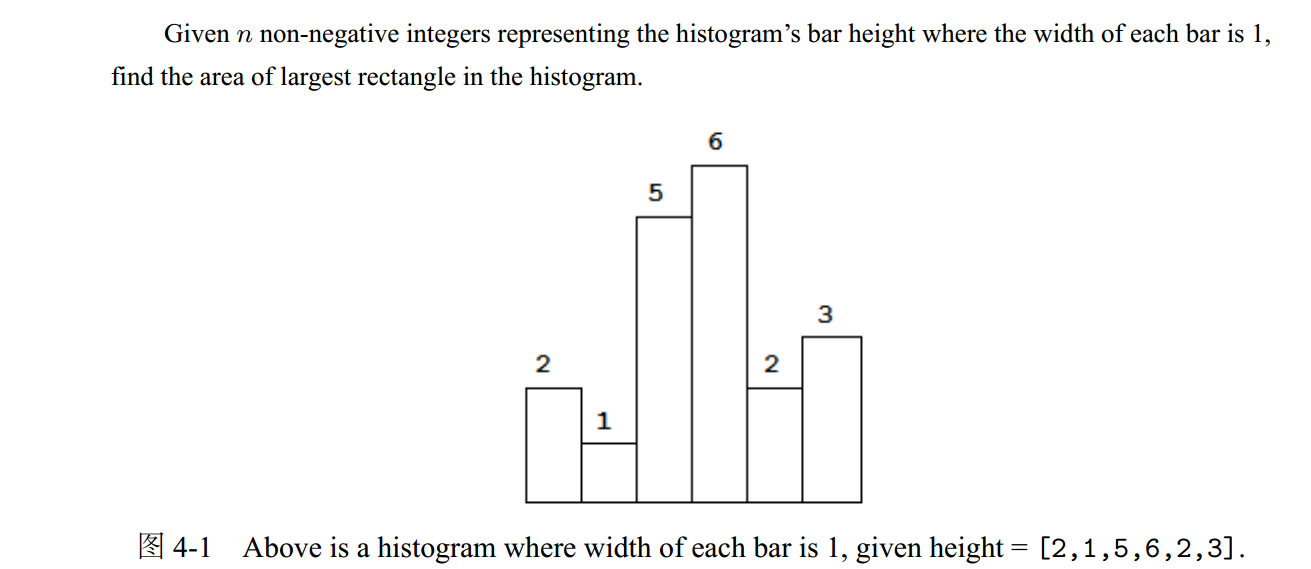
又是一道构思巧妙的题，暴力求解复杂度太高，通过构造一个递增栈来解决：如果当前元素小于栈顶元素，则说明栈内已经构成一个

递增栈，则分别计算以每个元素为最低值的面积；反之，则入栈。

int largestRect(vector<int> &height)
      {
          stack<int> s;//定义一个单调递增栈
          height.push_back(0);//定义单调递增栈的最后一个
          int result = 0;//记录当前最大的面积
          for (int i = 0; i < height.size();)//满足条件i才递增
          {
              if (s.empty() || height[i]>s.top())
              {
                  s.push(i++);//只有当前元素大于栈顶元素是才入栈相应的序号，构造递增栈
              }
              else {
                  //当前元素小于栈顶元素时
                  int tmp = s.top();//保留栈顶元素
                  s.pop();//弹出直至当前元素大于栈顶元素，使栈仍然是递增的
                  //
                  result = max(result, height[tmp]*(s.empty() ? i : i - s.top() - 1));
              }
          }

          return result;
      }

注：上述代码有误，应该是height[s.top()]