UFLDL（五）自编码算法与稀疏性

     新教程内容太繁复，有空再看看，这节看的还是老教程：

     http://ufldl.stanford.edu/wiki/index.php/%E8%87%AA%E7%BC%96%E7%A0%81%E7%AE%97%E6%B3%95%E4%B8%8E%E7%A8%80%E7%96%8F%E6%80%A7

 

     之前讨论的神经网络是在有监督的学习中的应用，而自编码神经网络是一种无监督的学习算法。它的特点是使用了BP，并且把输入值当作目标值。

     当隐藏层单元的个数小于输入的个数时，相当于完成了降维，而当输出时，又相当于重新恢复。

      

      为了给隐藏单元加入稀疏性限制，可限制隐藏单元的平均活跃度，让其接近于0：

      

     在优化目标函数时，可通过加入惩罚项来对其进行限制（类似于防止过拟合的方法）：

     

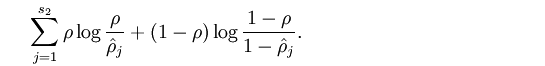
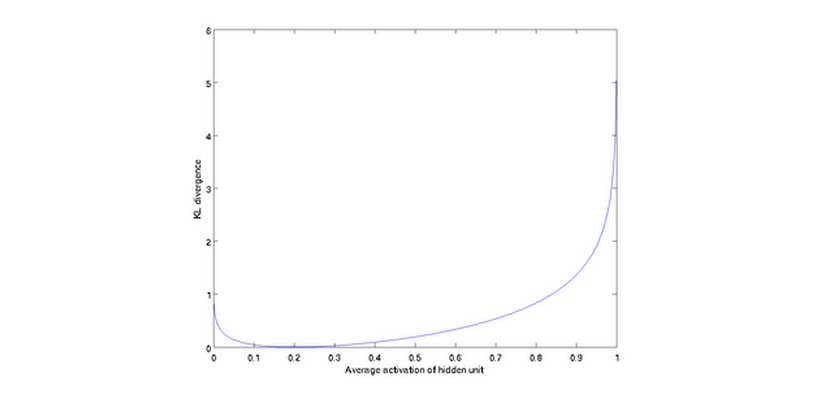
     里面的那个式子叫相对熵，它的性质如图所示：在两变量相等时值最小为0；随着两变量差异变大值也递增。因此，

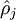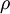最小化这一惩罚因子具有使得  靠近  的效果。

     

     总体代价函数可如下所示：

     

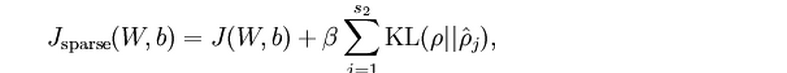
     结合前面的后向传播算法，第二层的残差可替换为：

     

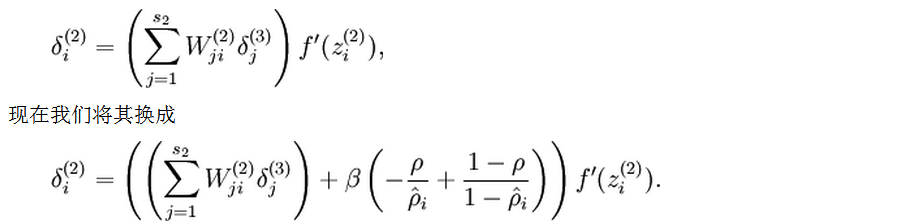
      关于替换的推导，可参考：http://blog.csdn.net/itplus/article/details/11449055

     关于自编码和稀疏编码，可参考：http://blog.csdn.net/on2way/article/details/50095081以及http://blog.csdn.net/on2way/article/details/50389968